Yet another option has come to mind in connection with fitting optimized floating-point types, with 36-bit, 48-bit, and 60-bit lengths, all multiples of 12, into our 8-bit and 64-bit world.
Given that we need to build computers using standard DRAM modules that are 64 bits wide, let us begin by admitting that shrinking the double-precision floating-point number to 60 bits is an unnecessary indulgence.
But we still want to expand the single-precison floats from 32 bits to 36 bits to make them usable, so we still need to have 12 bits as our basic unit.
In this scheme is that each 64-bit memory word is divided into five 12-bit memory cells, and it is the 12-bit memory cells that are addressed. This means that for it to be useful, an efficient means of dividing addresses by five is required. Possibly, using a mixed-radix representation of addresses and index values would be a reasonably efficient substitute.
The left-over four bits of each memory word, though, aren't wasted. Instead, they're used to add some extra precision to the floating-point number formats derived from the 12-bit unit, so that instead of being 36, 48, and 60 bits long, they're 38, 51, and 64 bits long. This does make it a bit complicated, and the EQUIVALENCE statement in FORTRAN, or the UNION in C will not permit one to do the same things that one could do with them on a more conventional architecture.
For simplicity in explaining what is going to be a rather complicated scheme of allocating memory, let us assume that we are dealing with a big-endian architecture.
This time, I am thinking of the following scheme: consider each 64-bit memory word to contain five 12-bit memory cells, plus four supplementary bits.
The basic rules that govern where the bits of a floating-point number of a given length are stored in memory are the following:
The third rule, for example, would allow intermediate results of a computation to be saved to a magnetic tape device which was organized around the 12-bit word. Doing so, however, would produce some loss of the least significant bits, the same as would result from saving the intermediate results in printed decimal format.
Thus, this could cause significant changes to those results of a simulation which are unreliable and invalid in any case, due to the underlying phenomenon being modelled being chaotic, just as happened with a simplified weather simulation on an LGP-30 computer that led to the original discovery of the "butterfly effect".
Fixed-point values could either be dealt with only using conventional addressing, where the 64-bit memory word is subdivided into units of 32, 16, and 8 bits, or one could have 12-bit, 24-bit, 36-bit, and 48-bit integers which make no use of the supplementary bits.
If one were to use the supplementary bits to allow the length of integers to be increased, I suppose that in order to have the supplementary bits increase the range of integers without disturbing their values, one would have 25-bit, 38-bit, and 51-bit integers where the supplementary bits are inserted between the most significant bit, which indicates the sign, and the next most significant bit. For two's complement integers, but also for sign-magnitude integers and one's complement integers, if the value of a 51-bit integer were to fit within a 48-bit integer, then taking the more visible 48 bits of the integer exclusive of the supplementary bits would give an integer of the same value. But when one was storing a 48-bit integer into memory exclusive of the supplementary bits, sign extension into the supplementary bits would be required.
If this latter option is chosen, or is available as one option, for integer values, then it would still be possible to use EQUIVALENCE or UNION to manipulate individual bits of a floating-point number, but only by equivalencing a 38-bit integer to a 38-bit float, or a 51-bit integer to a 51-bit float, and so on, then using integer arithmetic to manipulate individual bits. This is because the supplementary bits used with a value only depend on its length, and while the order in which they are used differs between integers and floating-point values, that order is consistent without regard for the alignment of the value. This would also mean that 64-bit integers are necessary. But then, computers these days normally use 64-bit addressing, and so including them in any case would seem inevitable.
Sometimes, however, computers operate on fixed-point data where the binary point is not located after the least significant bit. If, for example, the binary point were placed after the sign bit, so that fixed-point numbers were being treated as being in the interval [-1,1), then it would make sense to use the supplementary bits for the least significant bits. Usually, however, computers use the same basic instructions to handle fixed-point numbers wherever the binary point might be, with values of the same length but with different locations for the binary point not being treated as of different types.
As using fixed-point numbers to represent integers is by far the most frequent case, though, it makes sense to assign bits of data to the supplementary bits based on that case.
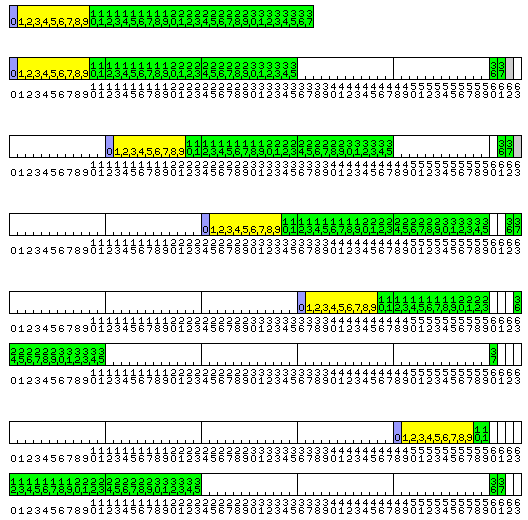
Let us assume that a 64-bit memory word is physically laid out as five consecutive 12-bit memory cells followed by four consecutive supplementary bits, associated with the first four memory cells. Then an aligned five-cell float would appear in storage with the bits in the same order as a 64-bit float in a conventional big-endian architecture built around the 8-bit byte and the 32-bit word.
Let us look at two words, numbered 0 and 1, in memory, each of which contains memory cells numbered 0 through 4, and bits numbered 0 through 63.
Let us see how, according to the rules noted above, a three-cell floating-point number which begins in memory cell 3 of word 0 would be stored in memory.
The most significant part (presumably including the sign and the exponent fields) would be in memory cell 3 of word 0, or bits 36 to 47 of word 0.
The next most significant part would be in memory cell 4 of word 0, or bits 48 to 59 of word 0.
The least significant whole memory cell would be memory cell 0 of word 1, or bits 0 to 11 of word 1.
Then the second least significant bit of the floating-point number would be the fourth supplementary bit in word 0, associated with memory cell 3, bit 63 of word 0.
Finally, the least significant bit of that number would be the first supplementary bit in word 1, associated with memory cell 0, bit 60 of word 1.
The following diagram illustrates the format of a 38-bit floating point number, and its five possible alignments in memory:

Note that one supplementary bit, shown in gray, is left unused in the first two of the possible alignments.
This diagram illustrates the format of a 51-bit floating point number, and its five possible alignments in memory:

Here, one supplementary bit is left unused only in the first of the five possible alignments.
Finally, the format of a 64-bit floating point number, and its five possible alignments in memory, are illustrated in the diagram below:

Here, the supplementary bits are fully utilized without wastage, since the length of the number corresponds to that of the memory word.
The foregoing has been concerned with explaining one of three views of memory that it is envisaged a system including what was described above would have: the extended 60-bit view.
There would also be a 64-bit view, where the computer operates as a conventional processor with 8-bit, 16-bit, 32-bit, and 64-bit data types. In that view, all the bits of a 64-bit memory word are visible, and no distinction is made between the leftmost 60 bits, used as conventional data bits in the extended 60-bit view, and the rightmost 4 bits, used as supplementary bits in the extended 60-bit view.
Although is has not been made explicit above, the choice of which bits in both floating-point numbers and integers that are 38, 51, or 64 bits in length in the extended 60-bit view to place in the supplementary bit is for purposes of compatibility between the extended 60-bit view and the plain 60-bit view.
In the plain 60-bit view, the architecture appears to the programmer as if the machine consists of 12-bit memory cells, and data types of 36, 48, and 60 bits are handled.
However, when a floating-point quantity of 36, 48, or 60 bits is stored in memory, the bits used as supplementary bits in the extended 60-bit view are still zeroed. When an integer quantity of 36, 48, or 60 bits is stored in memory, the bits used as supplementary bits are set either to all zeroes or to all ones, corresponding to the sign of the integer quantity.
Those bits are never read in this mode, and their contents are not visible to the programmer, but in this way quantities stored in memory in plain 60-bit mode will have the same value when read after switching to extended 60-bit mode.
Plain 60-bit mode is available to provide compatibility with systems that operate natively with a 48-bit word and datatypes of 36, 48, and 60 bits in length. Given that a fast divide-by-five circuit is helpful to an implementation of this architecture, a fast divide-by-three circuit is likely also to be available, which would allow an implementation of triple-channel memory.
That would mean the same chip could turn off the divide-by-three circuit, operate natively with a 192 bit wide path to memory, and then use the divide-by-three circuit to operate as a conventional architecture with power-of-two lengths for all primitive data types, and also have the plain 60-bit mode and extended 60-bit mode both to facilitate communications between the native 48-bit mode (which is how operation with the divide-by-three circuit turned off will be called here) and the 64-bit mode and to provide additional precision where 38, 51, and 64 bit floats are better suited to a particular problem than either 36, 48, and 60 bit floats or 32 bit and 64 bit floats.
A computer with four radically different modes of operation might suggest that programs running in these different modes could check on each other's activity in some way, as it might be more difficult to tamper with them all at once.
This, however, is basically security by obscurity; a technique like Secure Memory Encryption, where executable code in memory is encrypted with a different key for each program, as offered by AMD on their EPYC and Ryzen PRO processors, clearly is more likely to provide genuine security.
However, there's another possibility to consider:
17 * 3 = 51 18 * 2 = 36 19 * 2 = 38
If one uses a machine language resembling that of the IBM System/360 or the Motorola 68000, where program code is composed of 16-bit units, the data lengths provided in the scheme described here provide a potentially convenient way of associating either one, two, or three additional bits with each 16-bit unit.