Considering the matter in light of the different ideas used so far, and in light of the characterisics of modern DRAM systems, I think I have come up with something that can provide the benefits sought so far - in a very simple fashion, consistent with the way modern computer systems operate.
Let us suppose that we have a computer with 64-bit wide memory.
Given that DRAM is so designed that to use it at maximum bandwidth, it is necessary to access blocks of 16 consecutive locations at a time, I propose that one can make the memory appear to be composed of memory locations that are 96 bits wide at the cost of having to access 32 consecutive locations at a time.
When it is necessary to allocate a block of 96-bit locations, allocate two blocks of 64-bit locations, one with half as many locations as the other.
In this way, the physical memory addresses needed to allocate the data that goes into making up a 96-bit word are formed without the need for division by 3, and the data in a block of 96-bit words is accessed from the 64-bit wide memory at full speed; two blocks containing the first 64 bits of each word, and one block containing the last 32 bits of each word.
If one has internal cache organized around the 96-bit word, we can then have the cache organized in a dual-channel fashion so as to allow rapid access to individual unaligned words, which then permits 36-bit and 60-bit data to be accessed with only the trivial multiply by 3 and multiply by 5 operations, without divisions.
How about external physical memory?
Let us suppose it to be composed of DRAM modules that are 64 bits wide, which, to be read efficiently, need to be read in groups of 16 consecutive words, these groups being aligned on 16-word boundaries.
However, it is possible, after requesting that such a group of words be readied for reading, to read the one you are most interested first.
The desirable, and apparently attainable, characteristics of such an organization of memory are to be:
First: it is possible to read, in parallel, every part of an unaligned operand, at least up to 60 bits in length, so that if one must read an individual data item, even if it crosses block boundaries, there is no speed penalty.
Second: at least for sufficiently large blocks of 96-bit words, they can be read from the memory system at its full bandwidth, with no inefficiency.
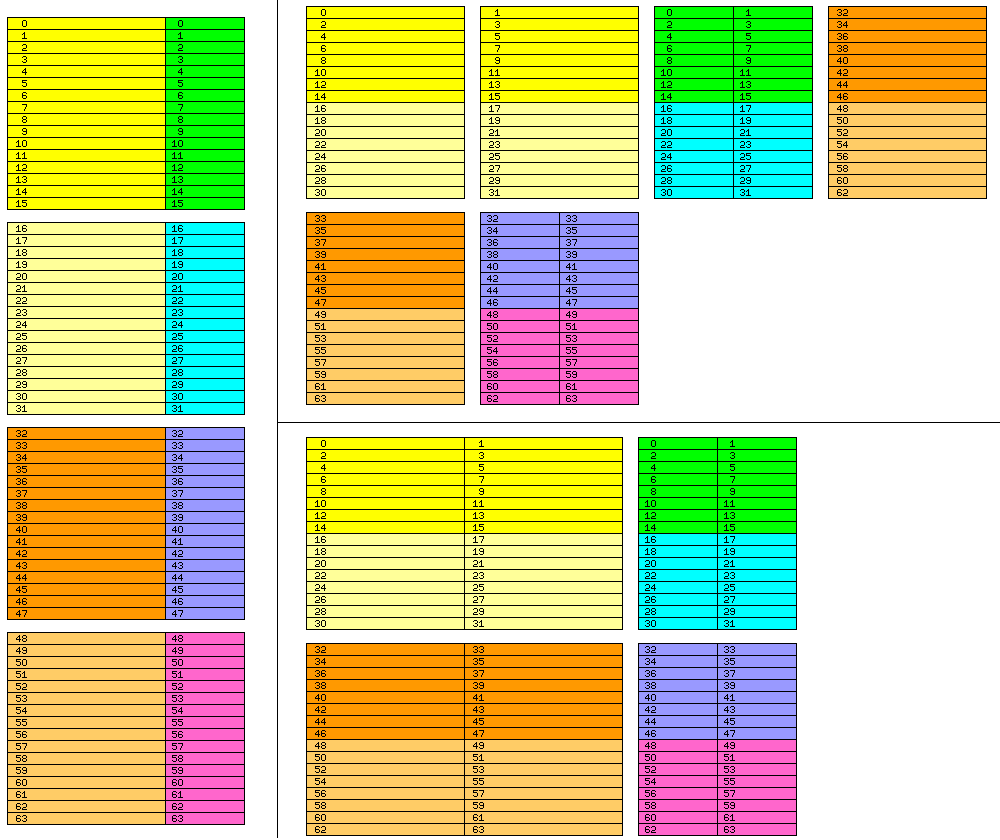
It took some thought to figure out exactly what was needed to attain this, but the diagram below shows two arrangements which satisfy those conditions:

The diagram is divided into three parts.
The left side of the diagram shows how the memory will look to the programmer, as a sequence of 96-bit words with consecutive addresses. As a reference to the two parts on the right side, the words are divided into a 64-bit part on the left, and a 32-bit part on the right, each with an identifying color for each group of 16 words.
The top right side of the diagram shows how, using quad-channel memory, data can be organized to meet the conditions outlined above.
This layout has the advantage that it is primarily built around the most common case, of using data that is 32 bits and 64 bits long, and addressing data built around the 12-bit unit only requires multiplication by 3 and 5, which is a trivial operation.
It has the disadvantage that one would have to access a block of 128 words that are 96 bits long in order to retrieve it from memory with 100% bandwidth efficiency, which is a significant increase in block size.
The bottom right side of the diagram shows how an asymmetrical dual-channel arrangement, those two conditions can also be achieved.
Here, the memory design is oriented towards the 96-bit word, and division by 3 is required to access conventional data in the 32-bit or 64-bit sizes. However, this is not a serious problem; Intel made Xeon systems with three-channel memories.
For full-bandwidth accesses, only blocks of 32 words of 96 bits in length, and of 48 words of 64 bits in length, are needed.
Of course, another memory architecture that could work would be a strictly conventional dual-channel memory arrangement, where each of the channels is 192 bits wide, as shown below:

On further thought, re-examining why a naïve attempt at a simple dual-channel memory arrangement could not be made to work, a bolt of inspiration came, and I came up with this:
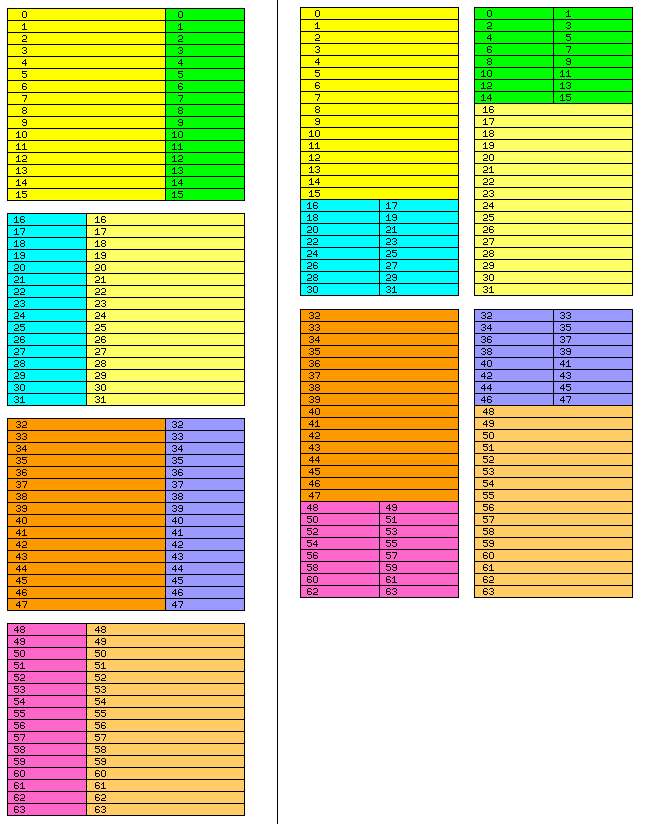
By splitting up alternating blocks of 96-bit words into either a 64-bit part and a 32-bit part, or a 32-bit part first, and then a 64-bit part, I am able to make it possible for blocks of 32 words, 96 bits in length, to be read at full bandwidth, and, when it comes to unaligned data, not only are the first and second parts of word 15 in opposite channels, but the second part of word 15 is in the opposite channel from the first part of word 16.
However, while this meets one of the basic conditions for handling unaligned data, it doesn't quite work: since the second part of word 15 is only 32 bits in length, it could be in the middle of an unaligned data item that was 60 bits long.
But the way to fix that is obvious. Instead of interpreting the diagram as showing how a series of 96-bit words can be stored in dual-channel memory, each channel of which is 64 bits wide, double the width of everything, with the programmer's representation on the left showing 192 bit words, divided into 128-bit and 64-bit parts in alternating orders, and the physical memory representation on the right being applied to dual-channel memory, each channel of which is 128 bits wide.
Finally, with the application of a little ingenuity, a solution that works with memory oriented around the more common case of the 32-bit and 64-bit world, which only requires two channels, and is thus reasonably simple.
However, there is another imperfection in what is shown in the diagram. It is not only the width of the memory words that needs to be doubled - the length of the blocks of memory words also needs to be doubled. Since the DRAM modules are optimized around fetching words in batches of sixteen, the organization of physical memory shown in the right-hand side of the diagram has to have, as its smallest basic division, groups of sixteen memory words, not, as shown here, groups of eight.
So while one can follow the basic pattern shown, it will be necessary to lay out the scheme in terms of thirty-two consecutive 192-bit words being divided into a 128-bit part followed by a 64-bit part, followed by thirty-two consecutive 192-bit words being divided into a 64-bit part followed by a 128-bit part, and so on.
1 + 2 is 3, so that is why this technique works for 24, 48, and 96 bit data. 1 + 4 is 5, so a similar technique could be used for 20, 40, and 80 bit data, and 1 + 8 is 9, so this scheme could also be modified for 36 bit and 96 bit data.
The 36 bit word is indeed one of those that is desirable for purposes of emulation. Intel's temporary real is 80 bits long, and 20 and 40 bits would be relevant for emulating the GE 235 and GE 245.
But 15, on the other hand, is not a number of the form 2^n + 1, and so we appear to be left with more elaborate techniques for the 60-bit word of the Control Data 6600 and related machines - such as the one implicitly referred to above, support the 48-bit word, and use the ability to handle unaligned operands to go further and also handle 36-bit and 60-bit data.
Other options do exist, however. Using quad channel memory, one could make use of the fact that 60 is equal to 36 plus 24; use two channels to support a block of 36-bit words, and the other two to support a block of 24-bit words, and then exchange the two pairs of channels. This is, however, likely to be complex and unwieldy, leading to a large minimum block size for full bandwidth efficiency.
The illustration below shows how this would work,

and it can be seen from it that it is essentially equivalent to what one would obtain by directly using the fact that 15 is equal to 8 + 4 + 2 + 1.
The left side of the diagram shows the appearance of memory to the programmer as an array of 120-bit words, and how those words are divided to be placed in physical memory, and the right side of the diagram shows the layout of data in physical memory, organized as a four-channel memory with each channel being 64 bits wide.
Even from the diagram as it is, we can see the most significant drawback of this scheme: as the size of the block of memory that must be read to maintain full bandwidth is quite large, usually there will instead be bandwidth that is lost.