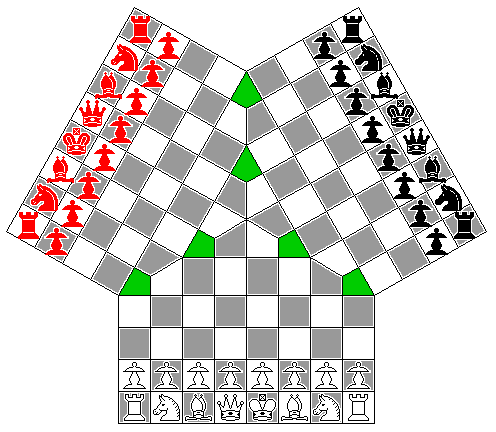
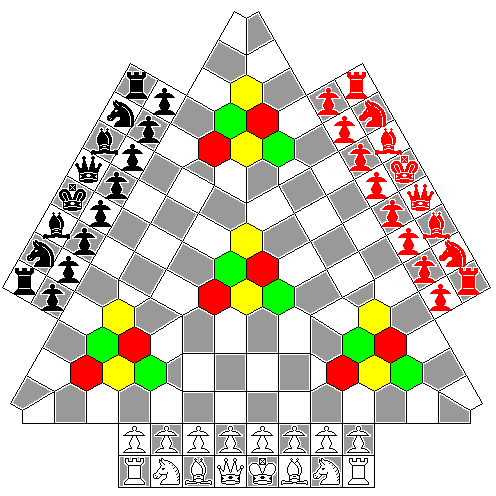
This game was designed by S. Waider of Vienna in the same year, 1837, in which he designed a variant of four-player Chess. It has a board that is attractive in appearance, because instead of subjecting the squares to extreme distortions, they are merely slightly stretched into rectangles, or cut where they reach the border between the parts of the board associated with different players.

Modern sources give a limited description of its rules, but the book Chess Eccentricities by Major George Hope Verney describes it more extensively, although still not perhaps as completely as the modern reader might like.
The board and setup for this particular game also adorn the cover of that book. The arrangement of the different colors of chessmen is that shown in the illustration given within the book where the game is described, and which is also confirmed by the text of that description; the illustrations on the cover of the book and on its title page have the black pieces to White's left (Queenside) and the red pieces to his right instead.
Castling and the double first move of the Pawn are present as in normal Chess. The order of move is described as "from left to right", while I would be inclined to take that as meaning counter-clockwise, I do not have to guess. Turning to the description of Major Verney's own four-handed Chess, its order of move is described as "from right to left", and as being identical to that of the card game of Whist. The order of play in Whist is clockwise, as is easily ascertained, and thus that guess is confirmed.
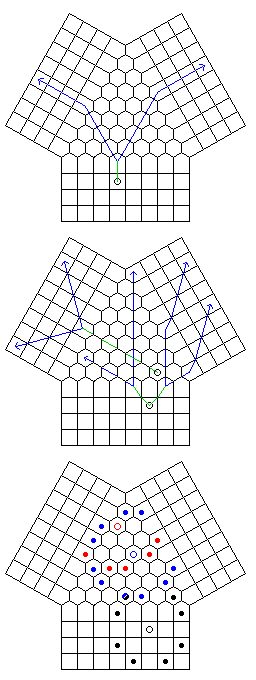
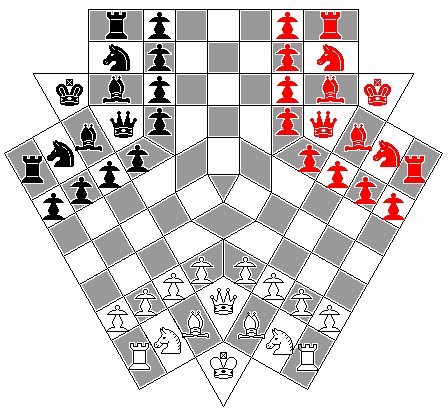
That description also gave two examples of how the men may move. Based on the brief statement that the men can change direction when they cross the boundaries between the three regions of the board, I speculated as shown in the diagram below on their moves:
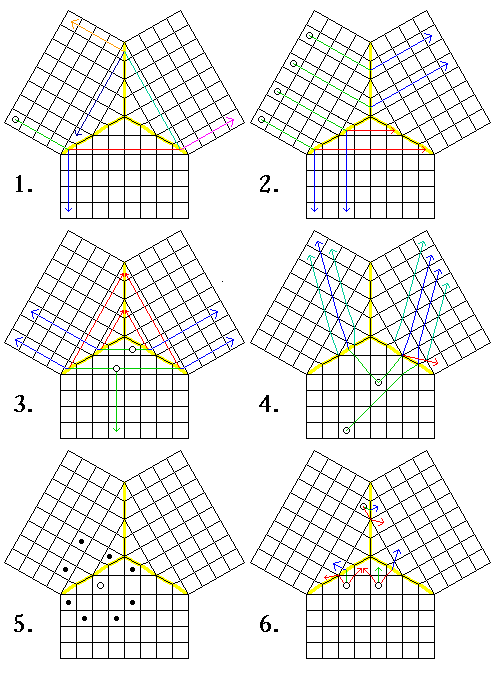
Diagram 1 shows what I thought the ability of the Rook to change direction at the boundaries between regions (shown by a yellow inverted Y in each diagram) might lead to. It seemed obvious that giving this sort of power to the pieces would be excessive, and so diagram 2 shows a more reasonable interpretation of the Rook's move, allowing it to cross only one boundary in a turn. The example for the Rook given in Chess Eccentricities seems to imply that the first alternative for the Rook's move, shown in blue, rather than the other alternative shown in red, is the one intended.
But what about the Rook hitting the boundary from the other direction, as shown in diagram 3? It would seem that neither the blue nor red paths shown are consistent with the other case; instead, the proper direction would be an outwards one making a very small angle with the boundary between regions, and thus no continuation beyond the boundary is available when the boundary is approached from that direction.
In diagram 4, we see the Bishop. On the right side of the diagram, the blue lines show my speculations for the Bishop's move past the barrier, and one red line shows an alternate possibility. On the left side, the blue line shows my speculation for the Bishop's move. Next to it, however, are two dark blue-green lines which correspond to the example given in Chess Eccentricities for the Bishop's move.
This told me what was wrong with how I conceptualized the board. I had thought of the spaces shown in green in the diagram of the chess board as being treated as ordinary squares. It was clear from the fuller description that pieces were never allowed to stop on those squares, but they would still pass through them, and change direction on the boundary lines treated as geometrical lines of zero thickness. But that was not, apparently, Waider's intent. Instead, the green areas ought to be thought of as voids, gaps in the board, not as squares belonging to it, for the purpose of defining moves, even if it is possible to pass through those voids. Another way to put it would be to divide each one into a small black triangle and a small white triangle.
The dark green lines have the advantage over the blue line of my speculation that they continue along the same color of square as the Bishop's initial move on its home board.
If that is to be taken as a general principle, then the blue lines need to be rejected for the Bishop's move on the right side of the diagram as well. But the corresponding dark blue-green lines seem very hard to justify as possible continuations of move. The one red line does maintain the color of the squares moved upon, and it is a logical continuation of the move that leads to it, but it seems to apply to only one of the three possible cases, and is in a different direction from the one example that I have. Perhaps, if the blue-green lines are hard to justify, one might interchange the assignment of the two blue lines?
Diagram 5 shows my attempt to deal with the Knight's move from one position, and diagram 6 shows the possible cases for two White pawns and one Red pawn.
My modern abstract geometrical temperament seems to have placed me so far out of sympathy with S. Waider's philosophy of movement that I cannot guess which way the pieces should move in this game, try as I might. What if a simpler rule were applied to this board, one where pieces move up to the squares with one side slanted that abut the boundary, and then, regardless of what type of piece they are, always cross the boundary with a single-step move along what might be thought a Rook line to the corresponding square on the other side of the boundary?
This would have the advantage of eliminating the possibility of arguments over legal moves, but it would make the boundaries into obstructions that would be too easy to block. Perhaps that might be helped by expanding the board somewhat:
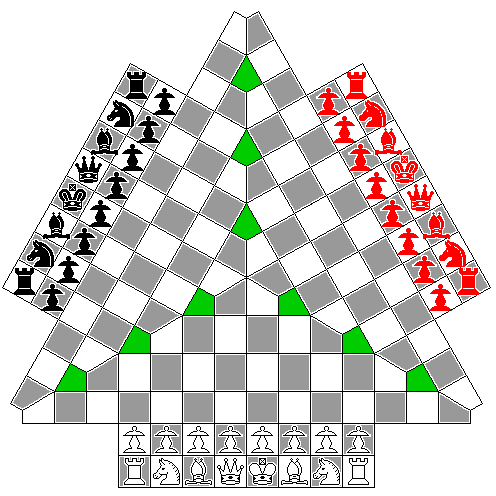
But then I think that perhaps he should have instead bit the bullet and gone instead with this arrangement:
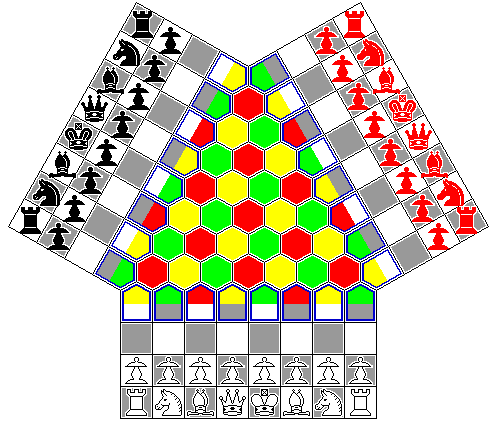
Since Pawns and the King make only single-step moves, for them to change to the Wellisch moves when entering the central part of the board, suggested in the case of the Pawn by that part's orientation relative to the wings of squares, would cause no problem. As to the other pieces, moving in the central part with the geometrically analogous moves as used by I. G. Shafran, Wladyslaw Glinski, H. D. Baskerville or Helge E. De Vasa would seem to be appropriate. Even allowing the pieces to continue moves through the boundary squares, outlined in blue, rather than simply going to those squares, and continuing from them with a conventional Chess move to the outer wings, or a Hexagonal Chess move inwards is not insuperable, although given that a hexagon has six sides instead of four, in some cases there will be two choices for continuing a move.
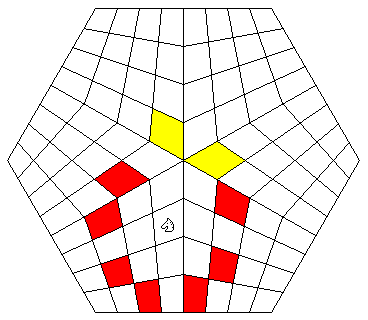
It might also be noted that one alternate board design for Game of the Three Kingdoms suggests it is a board of this type, but I think the dotted lines there, even though they cross each other, were simply there to indicate the single step in which the river was crossed, rather than creating additional points for movement.
Thus, in the image on the left, the diagram on the top shows how a Rook's move might be continued. The uniformity of the transition from square to hexagonal and back again means that one Rook can illustrate all the possible rules.
The second diagram shows how the Bishop can be treated. Here there are also some cases where there are two choices of continuation at the transition. But in going from the hexagons to the squares, if the change in move must occur on the boundary square and not the preceding hexagon, there are cases where a diagonal move must halt at the boundary because of inherent ambiguity.
While one Bishop illustrates all the basic cases, a second one is still helpful to show the one situation where there is an extra choice of move when going from hexagons to squares, instead of the other way.
The move of a Knight from a boundary square is obvious; it needs to use the square-board rule for moves into the square board, and the hexagon-board rule for moves into the area of hexagons. Slightly away from the boundary is where the complexity lies.
Moving from squares to hexagons, there are plausible continuations of the Knight's move. But it appears that a Knight on a hexagon, as opposed to one of the boundary spaces, simply cannot continue its move to a square. In some cases, because of the inherent ambiguity, no move suggests itself, and in others, where a move does appear reasonable, that move could also be interpreted a diagonal or orthogonal move of two spaces, which seems an inappropriate thing to assign to a Knight.
But if one is going to use hexagons, the argument would be why bother with having part of the board using squares; why not simply go to a completely hexagonal board for three-player Chess, as Wellisch was the first to do?
That is not to say the idea of a transition from a square board to a hexagonal one is useless. It could be used for a game of Chess on the faces of a cuboctahedron, or in squares, triangles and/or hexagons in an Archimedian tiling, or even part of a Socolar tiling.
Will I descend to the very pits of madness required to propose rules for Chess on a Penrose tiling? The only thing that can be said is that I have not done so quite yet. However, it might be just barely possible to do so, if one used the rhomb tiling, and one made no attempt to describe moves on other than Rook lines. So one might have pieces that moved like a Rook, but for varying numbers of steps, either always entering and leaving a rhomb by opposite sides, or having the privilege of changing direction during a move. Instead of Pawns, one would have Wazirs. Edgar Rice Burroughs' Martian Chess, Jetan, is one example, and some wargames on an enlarged square board would provide other examples, of how one could make a game resembling Chess with such a limited variety of movement.
One might think of a board like the following as a way to apply the principle of a hybrid square/hexagonal lattice to Waider's board that would be closer to his original conception of three abutting boards of squares with only slight interruptions:
but, I fear, not seriously.
Many years later, one Henry J. Self devised a three-player form of Chess which avoids all ambiguous cases by leaving a triangular hole in the middle of the board:
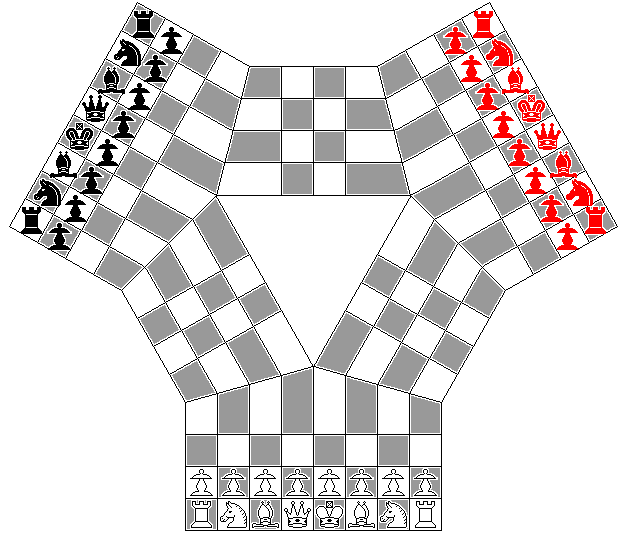
Except for the size of the hole, geometrically it closely resembles the Chinese Game of the Three Kingdoms; a more exact analogue of that game as applied to our chess had been devised by Robert Zubrin and others much later.
Given that the chief problem with the chess board devised by Waider is that the frequent gaps in the layout require allowing pieces to make unusual moves if a reasonable amount of piece mobility is to be obtained, if more orientations of normal squares were admitted to the layout, then the slopes of the interfaces between areas of normal squares would be smaller, requiring less frequent interruptions.
Thus, a board like the following, inspired by the method I used to simplify drawing the board devised by Henry J. Self above:
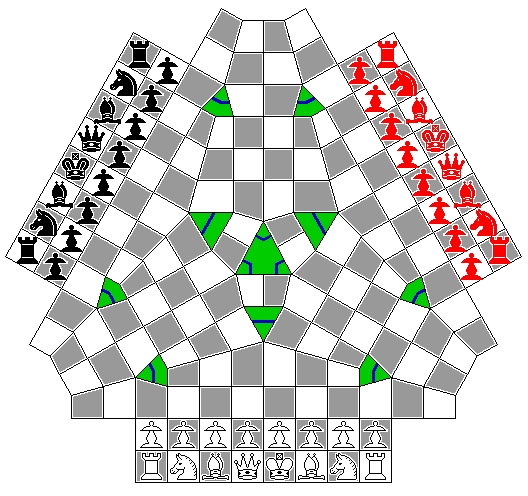
could perhaps provide a reasonable board for chess for three players in which squares might be turned into rectangles, and/or have one side sheared off at an angle, but no more extreme distortions are found.
In order that the Rook Pawns are able to advance normally, some orthogonal moves must be allowed through the green areas, but only the most obvious ones, as indicated by the blue lines. Diagonal moves are only allowed that proceed in the normal way, through the adjoining corners of like-colored squares, and from one corner to the opposite corner, avoiding each green area completely, as in Self's game. Thus, while the Bishops, from their starting squares, can move up to four steps diagonally towards the nearer edge of the board, and up to seven steps diagonally towards the further edge of the board, the Queen, from her starting square, can only move two steps diagonally towards the Queen's Rook, and may only move three steps diagonally to the Kingside, being blocked in each case from further progress by the green areas on the board.
The extra two files beyond the initial arrays, and the three two-square paths through the center of the board, could be omitted, but then, except for the green areas on the Rook files, the board would not look much different than that for Self's game, and the intent is to create a game which instead is similar to Weider's, but without the need to allow some implausible piece moves that would be hard to remember. The presence of these areas on the board means that Pawns can, by capturing, reach squares on which they cannot advance short of the opponent's back rank. Rather than adding elaborate rules where a Pawn might be able to move diagonally forwards on some of those squares without capturing, and sideways on others, I propose that Pawns also promote when they reach any such square, this being the simplest rule, and not an unreasonable one, given the size of the board.
The year 1837, in which S. Waider devised the game featured here in Vienna, also featured the invention by Coquelet in France of this form of Chess for three players:
Aside from being informed that this game allows the Bishops to change colors, I have no definite information on the moves. This board does not, however, pose difficulties of the magnitude posed by Waider's board, and thus reasonable inferences can be made for what the moves might be.
The first two diagrams show different orthogonal moves. The second two show diagonal moves. The diagram on the lower left shows in red two moves that might be thought of as diagonal moves, but I think they are unlikely to be allowed. The diagram on the lower right shows, again in red, two moves that presumably are allowed, being the two moves by means of which a Bishop might legitimately change color.
One thing that was noted in the information I have on this game is that not only do the Pawns have a double-step first move (despite having a board only seven ranks deep instead of eight), and are subject to en passant capture when using that privilege, but that Castling is allowed as well. Had the King's starting square been that of the Queen, it would be easy enough to see how Castling would be permissible in the precise form that it has in conventional Chess. Given the array as it stands, I can only conclude that Castling consists of the following two elements: a diagonal move by the King to either Knight's starting square, followed by the Rook on that side moving two spaces to jump over the King to the Bishop's starting square beyond.
The fundamental flaw, of course, in any form of three-player Chess is that two of the players can gang up against a third, and this reduces the extent to which it is a game of skill.
However, this has been addressed through a neutrality rule originated by Ilshat Tagiev. This rule stipulates that a player can only capture pieces belonging to another player, or place another player in check, if one of the following two conditions is satisfied:
The form of three-player chess that is occasionally seen available for sale these days has the board, initial array, and algebraic notation system shown below:
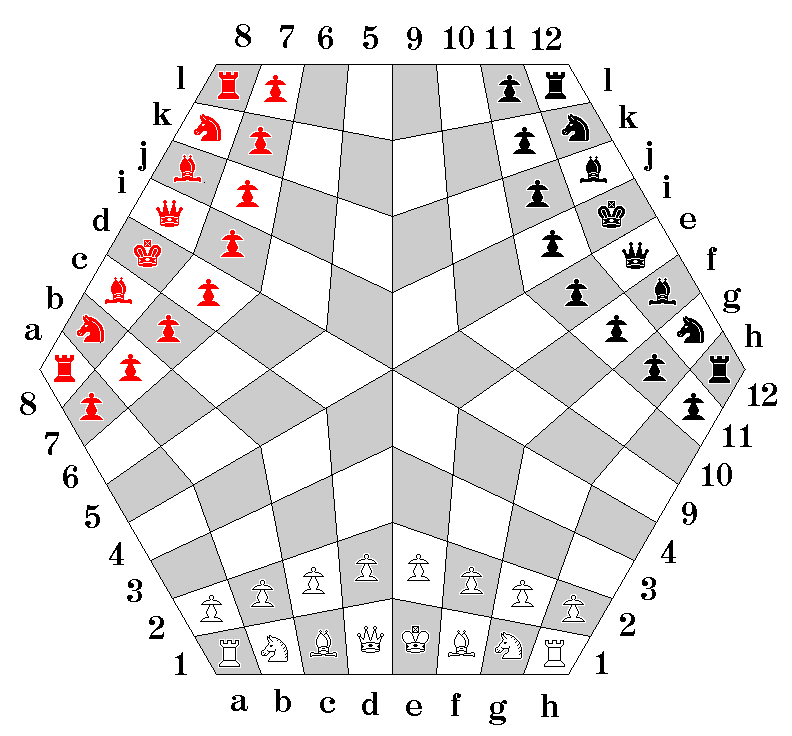
White moves first, the move proceeds clockwise from player to player, and note that each player's King is always counter-clockwise of his Queen.
Wikipedia, citing D. B. Pritchard's Encyclopedia of Chess Variants, credits the invention of this game to George R. Dekle, Sr., in 1964. This retired District Attorney, who calls himself Bob Dekle, (and so perhaps we should at least call him G. Robert Dekle, Sr., if we wish to be more formal) has recently published a book on chess variants, his own and others, titled Variations on the Theme of Chess, discussed on this page.
Obviously, this game is inspired by the Chinese Game of Three Kingdoms. However, aside from being based on Western chess rather than the Chinese game, there is one major difference in the rules: the game ends at the first checkmate, the mating player getting 1 point for the win, the mated player getting 0 points, and the remaining player getting half a point as if drawn. In The Game of Three Kingdoms, after the first checkmate, the General of the mated side is removed from the board, and the mating player continues to play, adding the pieces of the mated side to his own; the winner is the player who delivers the final checkmate. Because, of course, that was when the war ended, when there was one Emperor of all of China.
The manner in which the moves of the pieces are affected by the join between boards at the center is shown in the diagram below:
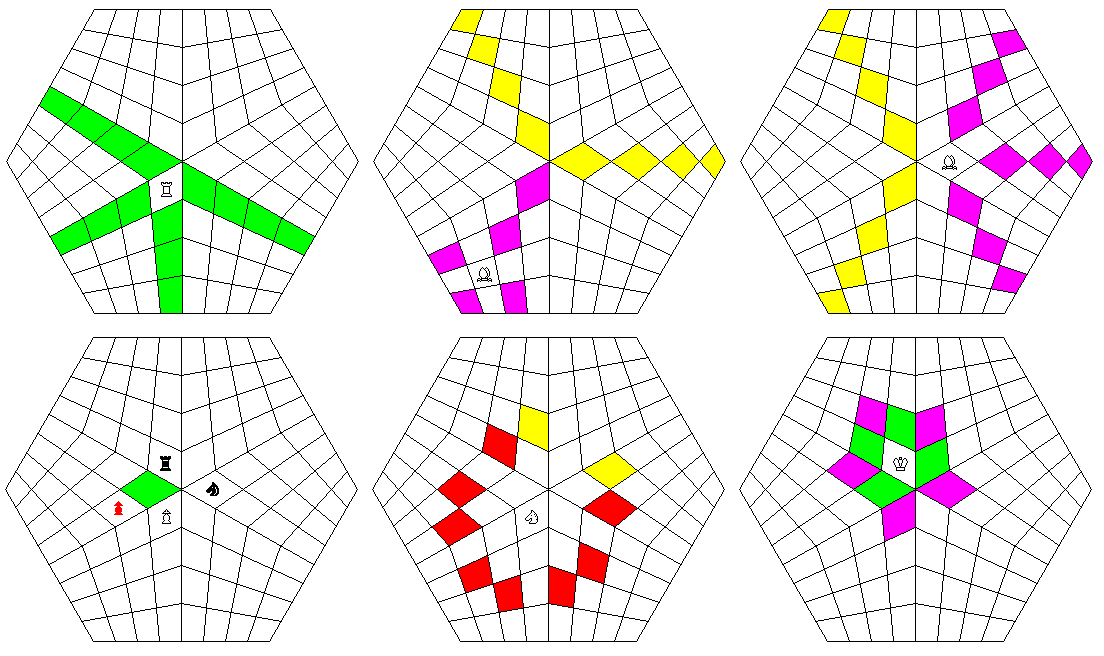
In the first diagram in the top row, it is shown that the orthogonal move of the Rook, as it passes through the sides of the squares and not their corners, is never really affected by the unusual nature of the center of the board.
In the second diagram in the top row, we see that the Bishop's move can be affected even if the Bishop is some distance away from the center, if it passes through the center.
In the third diagram in the top row, we see how the Bishop's move is altered if it is on one of the center squares.
In the first diagram on the bottom row, we see the moves of the Pawn from one particular center square; the green square is its normal forward move, and the red Pawn, and the black Rook and Knight are all pieces it could capture by moving one space forwards diagonally.
In the second diagram on the bottom row, we see how the Knight can move from one of the center squares.
In the third diagram on the bottom row, we see the King's moves from the center squares; the diagonal moves are shown in purple, and the orthogonal ones in green, matching the colors used to show the usual moves of the Bishop and Rook respectively.
Incidentally, the Knight's move can also be affected even if it is not sitting on one of the six center squares, as this diagram shows:
Robert Zubrin's Martian Chess follows the Chinese game more closely: the side with the last remaining King wins. However, when the first King is checkmated, while the other pieces of that side stay on the board, no one can move them; however, they can still be captured.
Obviously, if one has such a board, but wishes to play with only two players, the obvious thing to do would be to use opposite sides of the board for them. However, it is possible to go a step further:
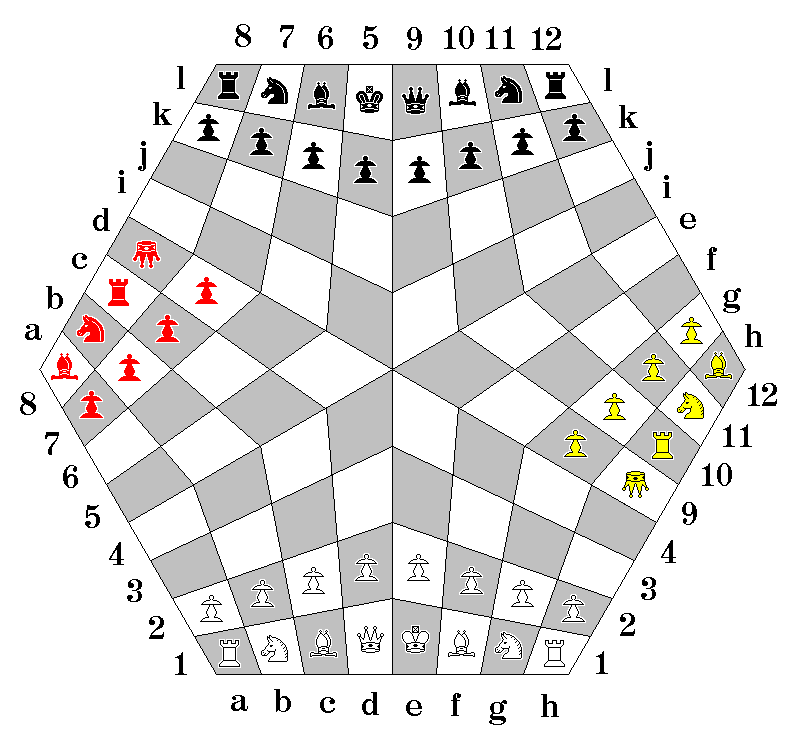
Here, the positions of the Black King and Queen are reversed, in order to preserve the symmetry of the arrangement when eight additional Black pieces (shown as red) and eight additional White pieces (shown as yellow) are added to the board.
These pieces are in the arrangement used in four-handed Chaturanga. Except that the King obviously had to be replaced, since each side already had a King, and while a second Queen, along with a third Rook, a third Bishop, and a third Knight was not in itself unthinkable, the fact that the arrangement in four-handed Chaturanga put the King, a short-range piece, on the outside meant that putting a second modern Queen in that position would drastically alter the spirit of the game.
And so, instead, what I propose to place in that position is a Ferz, represented by an upside-down Queen symbol.