A common technique to increase the speed of memory systems, used from the early days of core memories, and still used today inside the chips that make up modern DDR2 memory modules, is interleaving.
When a memory unit takes a certain amount of time to yield a word of data, and it is connected to a bus which would allow data to be transmitted along it at a faster rate, multiple memory units can be connected to the same bus.
So that successive memory accesses are more likely to make use of different memory units, the low-order bits of the address of a memory word (instead of the high-order bits, the naïve case which does make it easy to connect an arbitrary number of memory units to the bus, one at a time, to increase capacity) can be used to select which memory unit is to be used.
This requires that the number of memory units involved will be a power of two, and that they are of the same speed and capacity.
So far, this is simple and obvious.
However, occasionally, in computations like matrix multiplication, a program will access data items spaced at regular intervals, but which are not consecutive.
A powerful computer system might use 16-way interleaving.
If one is multiplying two 16 by 16 matrices, and the length of a floating-point number matches the length of a memory word, then when one is fetching successive floating-point numbers from one of the two matrices, then one will take sixteen numbers from the same memory bank before going on to the next one, thus losing the benefits of interleaving!
One way to deal with that would be to store the 16 by 16 matrix inside a 17 by 17 matrix, thus avoiding this bad case in software.
This may not be feasible, however, in one very important case: on a vector supercomputer where the successive operations in multiplying a row of one matrix by a column of another matrix are initiated by a single instruction.
Incidentally, it may be noted that the ability of vector instructions to operate on regularly spaced numbers, known as "stride", is one of the critical supercomputer features that used to subject a computer to strict export controls; this illustrates how important this feature is in increasing the power of a computer.
One basic way to deal with this would be to interleave memory by using an odd number of memory banks that would be less likely than a power of two to be used as the size of a matrix or for any other purpose.
But if one used, for example, nineteen-way interleaving, then one would have to divide by nineteen and take the remainder to find out which memory bank to use.
Despite this, the Burroughs Scientific Processor used a form of this technique. Seventeen memory banks were connected together; each group of sixteen words was stored at one address in sixteen of those memory banks, leaving one word unused.
This meant that the quotient of division by 17 was not required to obtain the physical word address to use to find a given word of data; but the remainder of division by 17, applied to the physical word address (the logical word address, shifted right four bits to divide it by 16) was still required to determine the offset for a given row.
A technique involving multiplication by 15 was used instead of a true division by 17 to keep the addressing circuitry simple; I have not yet fully understood all the details of how this was done from the information available in my sources.
It should also be noted that, while the goal of avoiding conflicts through successive accesses to the same memory bank was similar, the BSP design was not connected with memory interleaving. The BSP was a SIMD computer with sixteen ALUs working in parallel; the intent was to ensure that successive operations could be parallelized, and would not require either the same ALU, or the same memory bank.
The crossbar switch between the seventeen memory banks and the sixteen ALUs addressed part of the problem. However, arithmetic operations normally have more than one operand; thus, for example, a collision could result from a matrix multiplication where, while the elements from a row of the one matrix are all in separate memory banks, the elements from a column of the other matrix are all in the same memory bank because of their stride. (Actually, because of the way FORTRAN stores matrices, the problem would occur with the rows instead of the columns.)
As long as they were in different memory banks, the crossbar network would take care of a situation where, say, the elements of the row were in memory banks 0, 1, 2, 3... and the elements of the column were in memory banks 7, 10, 13... by being rerouted with each step of the computation.
Of course, today, it will often be necessary for computer designers to use off-the-shelf parts. Thus, it may be that high-performance memory modules in the future will be sixteen-way interleaved; and, as well, interfacing considerations may prevent connecting seventeen of them to the same bus for an increase in speed through an additional level of interleaving.
One way to deal with that would be to rotate the locations of the words in each row of memory, so that in most cases, successive words in the same memory bank would be separated by a prime number.
The most obvious way would be like this:
------------------------------------------------------- | 0000 | 0001 | 0002 | 0003 | 0004 | 0005 | 0006 | 0007 | |------+------+------+------+------+------+------+------| | 0011 | 0012 | 0013 | 0014 | 0015 | 0016 | 0017 | 0010 | |------+------+------+------+------+------+------+------| | 0022 | 0023 | 0024 | 0025 | 0026 | 0027 | 0020 | 0021 | |------+------+------+------+------+------+------+------|
Here, illustrating the principle with eight memory banks, usually the memory words, the octal addresses of which are shown in their memory cells, in the same memory bank (the same column of the diagram) are separated by nine, instead of eight, in terms of their address.
If there were sixteen memory banks instead of eight, the separation would be seventeen, a prime number large enough to be little-used.
But note that the memory word from address 10 is in the same bank as the one from address 7; similarly, the one from address 20 is at the same bank as the one from address 17. Thus, we are paying the price of occasional bank collisions in the most common case of sequential access in order to solve what is, admittedly, a more severe problem, in the case of stride eight. But sequential access may be more than eight times, or more than sixteen times, as common as all the power-of-two strides put together.
For the CYDRA 5 system from Hewlett-Packard, a more elaborate method of modifying addresses in a pseudo-random fashion involving a shift-register sequence was used. While such a technique appears as if it would slow addressing considerably, methods were used to avoid significant delays.
In the case of eight memory banks, though, a trivial change could fix the problem; simply skew the other way, and instead of displacements of 9 and 1, we have displacements of 7 and 15, both better choices.
------------------------------------------------------- | 0000 | 0001 | 0002 | 0003 | 0004 | 0005 | 0006 | 0007 | |------+------+------+------+------+------+------+------| | 0017 | 0010 | 0011 | 0012 | 0013 | 0014 | 0015 | 0016 | |------+------+------+------+------+------+------+------| | 0026 | 0027 | 0020 | 0021 | 0022 | 0023 | 0024 | 0025 | |------+------+------+------+------+------+------+------|
With 16 memory banks, this would go from displacements of 17 and 1 to displacements of 15 and 33. However, while 15 is a better choice than 1, it still is more likely to come up than 17.
In thinking about this issue, I had come up with a simpler technique to avoid it, which is basically a more general form of this trick.
I wanted to continue to avoid any bank collisions for sequential accesses. As well, I wanted to avoid nearly all bank collisions for stride 16; I was going to design my example for the case of sixteen interleaved memory banks.
To avoid the wraparound problem, instead of having the case above where eight memory banks led to seven increments of nine and one increment of one, I would allow several other prime strides in addition to 17 to be spoiled by bank collisions.
The values I chose were 11, 13, 17 and 19. 11 is 16-5, 13 is 16-3, 17 is 16+1, and 19 is 16+3. These four choices would give me enough flexibility to work out a sequence which would close in on itself without any other displacements between successive rows of values except those three displacements which I felt were strides for which bank collisions were acceptable.
I worked out the sequence I needed like this:
1 1 1 1 1 1
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
* * * *
* * * * * * * *
* *
* *
0, 1 (+1, 17)
4 (+3, 19), 7 (+3, 19)
2 (-5, 11), 5 (+3, 19), 8 (+3, 19)
9 (+1, 17),
12 (+3, 19), 13 (+1, 17), 14 (+1, 17), 15 (+1, 17),
10 (-5, 11), 11 (+1, 17),
6 (-5, 11), 3 (-3, 13)
and back to 0 (-3, 13)
The displacements, in terms of memory bank location, from one group of 16 locations to the next, of words with addresses which are equivalent modulo 16, are illustrated below:
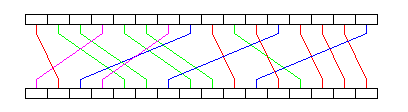
Thus, not only do we satisfy the two conditions that each of the 16 words in each group gets its own unique location in a different memory bank, and that only the four desired displacements are used, but also, the permutation is a cyclical permutation (one with only a single cycle).
Any ROM or logic circuit used to effect this type of addressing, of course, would take the last 16 bits of the address as input, and produce which memory bank to use as output, so the ROM contents would be the inverse of the sequence of numbers from 0 to 16 in the cycle:
0 | 0 1 | 1 2 | 4 3 | 15 4 | 2 5 | 5 6 | 14 7 | 3 8 | 6 9 | 7 10 | 12 11 | 13 12 | 8 13 | 9 14 | 10 15 | 11
By using the sequence of the cycle to assign memory words to the different memory banks, the permutation of addresses from which the cycle was derived can be achieved from one row to the next simply by a diagonal skew of the memory bank usage; that is, by adding successively increasing numbers to the number of the memory bank used from one row to the next.
Thus, the type of circuit used to implement this type of addressing would be:
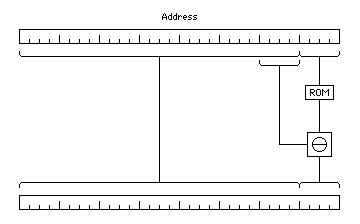
where the modular subtraction depicted in the diagram is subtraction modulo 16 (not addition or subtraction modulo 2, or XOR).
And so the words of data would end up being distributed in the memory banks like this:
0000 0001 0004 0007 0002 0005 0008 0009 000C 000D 000E 000F 000A 000B 0006 0003 0011 0014 0017 0012 0015 0018 0019 001C 001D 001E 001F 001A 001B 0016 0013 0010 0024 0027 0022 0025 0028 0029 002C 002D 002E 002F 002A 002B 0026 0023 0020 0021 0037 0032 0035 0038 0039 003C 003D 003E 003F 003A 003B 0036 0033 0030 0031 0034
and, thus, the difference in addresses from one row to the next would be either 11, 13, 17, or 19.
However, the differences between addresses separated by two rows can be 24 (11+13) or 36 (17+19), for example, thus occasionally causing bank collisions for those strides.
A simpler method might be, if we don't like the displacement of 15 caused by skewing by -1 instead of +1, would be to skew by -3. That would lead to thirteen displacements of 13, and three displacements of 29, each time. Or, one could try -5, giving us displacements of 11 and 27. Thus, -3 is probably to be preferred. Note that 13 plus 29 is 42, which, being a multiple of 7, is not too bad.
A thesis by Tuomas Järvinen discusses special permutations called stride permutations for use in permuted access; it is not clear to me if the advanced techniques proposed there or referenced there in earlier work are related to this quite simple scheme I illustrate here.
We saw earlier that when we tried to use a skewed distribution of memory addresses so that collisions would take place with a stride of 17, which could be avoided, we ended up with one collision at a stride of 1.
Suppose we follow the example of the Burroughs Scientific Processor, and use 17 memory banks for 17-way interleaving, using only 16 words out of every 17. Could we then shove the troublesome word out of the way?
What about a pattern like this:
000 001 002 003 004 005 006 007 008 009 00A 00B 00C 00D 00E 00F --- 011 012 013 014 015 016 017 018 019 01A 01B 01C 01D 01E 01F --- 010 022 023 024 025 026 027 028 029 02A 02B 02C 02D 02E 02F --- 020 021 ... 0EE 0EF --- 0E0 0E1 0E2 0E3 0E4 0E5 0E6 0E7 0E8 0E9 0EA 0EB 0EC 0ED 0FF --- 0F0 0F1 0F2 0F3 0F4 0F5 0F6 0F7 0F8 0F9 0FA 0FB 0FC 0FD 0FE
We still get a collision at a stride of 1 because 100 will follow 0FF in the first memory bank, but now that is much more rare.
With the rest of the last row moved over by one position, 102 follows 0F0, 103 follows 0F1, and so on. So at the changeover point, most of the new collisions are at stride 18.
Division by 17 isn't required for addressing, since each of the 17 memory banks would use conventional binary addresses.