Everyone is familiar with the basic operations of arithmetic, addition, subtraction, multiplication, and division. In the "new math" introduced during the 1960s in the junior high grades of 7 through 9, students were exposed to some mathematical ideas which formerly were not part of the regular school curriculum. Elementary set theory was one of them. Another was abstract algebra, in which it was illustrated that operations resembling addition and multiplication could exist that had some of their properties.
One of the simplest examples is modular arithmetic.
Here is an addition table, and a multiplication table, for modulo-6 arithmetic:
+ | 0 1 2 3 4 5 * | 0 1 2 3 4 5 ---------------- ---------------- 0 | 0 1 2 3 4 5 0 | 0 0 0 0 0 0 1 | 1 2 3 4 5 0 1 | 0 1 2 3 4 5 2 | 2 3 4 5 0 1 2 | 0 2 4 0 2 4 3 | 3 4 5 0 1 2 3 | 0 3 0 3 0 3 4 | 4 5 0 1 2 3 4 | 0 4 2 0 4 2 5 | 5 0 1 2 3 4 5 | 0 5 4 3 2 1
and here are the same two tables, but for arithmetic modulo 5.
+ | 0 1 2 3 4 * | 0 1 2 3 4 -------------- -------------- 0 | 0 1 2 3 4 0 | 0 0 0 0 0 1 | 1 2 3 4 0 1 | 0 1 2 3 4 2 | 2 3 4 0 1 2 | 0 2 4 1 3 3 | 3 4 0 1 2 3 | 0 3 1 4 2 4 | 4 0 1 2 3 4 | 0 4 3 2 1
Because 5 is a prime number, but 6 is not, if you eliminate the row and column containing zero from the multiplication table, for arithmetic modulo 5, but not for arithmetic modulo 6, you get a table where no number is repeated twice in any row or column. This means that if a number is not zero, in modulo 5 arithmetic, one can define the operation of dividing by that number. In both forms of modular arithmetic, one could define subtraction as well as addition.
Abstract algebra deals with three kinds of object: groups, rings, and fields.
A group is defined as: a set of elements, together with an operation performed on pairs of these elements such that:
A consequence of the third property is that there are no duplicate elements in any row or column of the operation table for a group. A consequence of the fourth property, together with the others, is that every finite group can be expressed as a set of permutations of n objects for some n, where the operation for the group is applying the second permutation to the elements of the first permutation.
There are many different kinds of finite groups, some with very complex structure. Most groups belong to families of groups with an infinite number of members. Thus, addition modulo 5 yields the cyclic group of order 5, and there are cyclic groups of every integer order starting with 2. However, there are 26 groups that don't belong to these infinite families, called sporadic simple groups.
A ring is a set of elements with two operations, one of which is like addition, the other of which is like multiplication, which we will call add and mul. It has the following properties:
Addition and multiplication modulo 5 and modulo 6 both yield rings. Matrix multiplication also leads to rings as well.
A field is a ring in which the elements, other than the identity element for addition, and the multiplication operator, also form a group.
There are only two kinds of finite fields. One kind is the field formed by addition and multiplication modulo a prime number. The other kind of finite field has a number of elements that is a power of a prime number. The addition operator consists of multiple independent additions modulo that prime. The elements of the field can be thought of as polynomials whose coefficients are numbers modulo that prime. In that case, multiplication is polynomial multiplication, where not only are the coefficients modulo that prime, but the polynomials are modulo a special kind of polynomial, known as a primitive polynomial. All finite fields, but particularly those of this second kind, are known as Galois fields.
Finite fields whose number of elements is a power of 2 have the bitwise exclusive-OR operation as their addition operation. This page explains why such fields are found useful in cryptography.
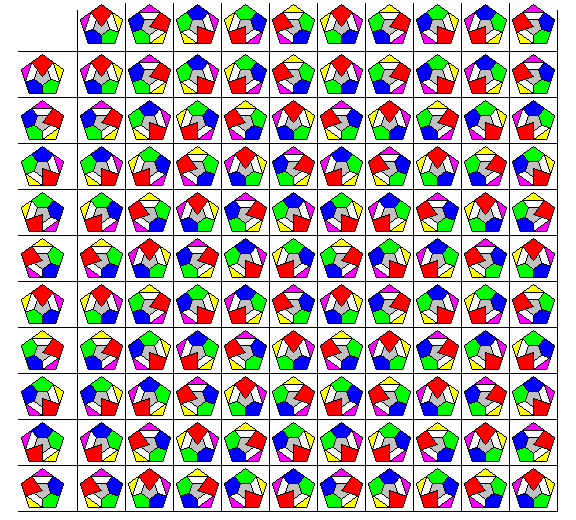
One of the simplest families of non-Abelian groups (or non-commutative groups) are the dihedral groups: these are the groups that involve both rotating a polygon with distinct corners (and thus, they have the cyclic group of addition modulo n, where n is the number of corners, as a subgroup) and also flipping it over. Since flipping the polygon over makes its previous rotations have the effect of a subsequent rotation in the opposite direction, this group is not commutative. The dihedral groups of order 3 (the dihedral group of order 3, D(3), is also the permutation group of order 3, S(3)) and order 4 are often seen in introductory books on abstract algebra: here is a colorful illustration of the table for the dihedral group of order 5:

Each symbol can be thought of as standing both for one position of the pentagonal card, and as the rotation with a possible flip that obtains that position from the starting position, with red pointing upwards and yellow pointing to the right. The symbol in the leftmost column indicates the first manipulation, and the symbol in the top row indicates the second manipulation.
If we replace the ten colorful symbols in the picture by the ten digits, though, it might be easier to see the group's structure, although the symbols in the picture show the group's origin in rotations:
| 0 1 2 3 4 5 6 7 8 9 ------------------------ 0 | 0 1 2 3 4 5 6 7 8 9 1 | 1 2 3 4 0 9 5 6 7 8 2 | 2 3 4 0 1 8 9 5 6 7 3 | 3 4 0 1 2 7 8 9 5 6 4 | 4 0 1 2 3 6 7 8 9 5 5 | 5 6 7 8 9 0 1 2 3 4 6 | 6 7 8 9 5 4 0 1 2 3 7 | 7 8 9 5 6 3 4 0 1 2 8 | 8 9 5 6 7 2 3 4 0 1 9 | 9 5 6 7 8 1 2 3 4 0
The alternating group of order 5, which is also the group formed by the possible rotations of a dodecahedron, has this page just about to itself.
Another interesting class of groups is based on directly considering the rules by which groups are built.
For example, the free Burnside group with 2 generators and exponent 3, which has 27 elements, is formed as follows:
One starts creating the group by beginning with two elements, a and b. The result of performing the operation associated with the group is usually just the concatenation of the names of the two elements: a "op" b is ab.
However, there is one rule making the group more than merely an arbitrary collection of strings: for any string s, sss is equivalent to nothing.
The group also has an identity element, represented by 0, such that 0 op s = s op 0 = s.
Also, because it is a group, if x op y = z, then q op y = z implies q = x, and x op q = z implies q = y. This rule is important to keep in mind, because otherwise this group would have an infinite number of elements, because there are an infinite number of strings made up of just a and b that have no sequence in them repeated three times. But while the potential number of elements of this group is infinite, this rule shows that they all belong to a limited set of distinct categories, or equivalence classes.
For example, aa when followed by a makes the null string, but that is equally true of babab or abaabaab, so aa, babab, and abaabaab must all be equivalent.
The possible distinct strings are noted by single letter symbols for compactness using the representation shown in the following table, which also includes several important string equivalencies:
0) the null string a) a g) aba babbab bbaabb A) aa babab G) bab abaaba aabbaa b) b h) abba baab B) bb ababa H) aabaa bbabb c) ab i) abaa C) bbaa abab I) abbaa aabab baaba d) ba j) babb D) aabb baba J) baabb bbaba abbab e) abb baabaa k) aaba E) baa abbabb K) aabba babaa abaab f) bba aabaab l) bbab F) aab bbabba L) bbaab ababb babba x) abaabb aabbab abbaba babaab baabba bbabaa X) babbaa bbaaba baabab ababba abbaab aababb
The identity element 0 is, of course, synonymous to any string repeated three times. The two remaining elements are noted by x and X, and have a large number of synonyms, as noted below:
In this notation, the table for the group is:
| 0 a b c d e f g h i j k l x A B C D E F G H I J K L X --------------------------------------------------------- 0 | 0 a b c d e f g h i j k l x A B C D E F G H I J K L X a | a A c F g D h k K H L d J l 0 e I B i b C E G x f X j b | b d B G f j a D L K H I c i E 0 A J C h l e X g x F k c | c g e C h L A B X f E G F H i a 0 x I K J D j k l b d d | d E G h D J L I x e F f g c b j X 0 K B A C l i a k H e | e h a J A E g x b l D j C f I c i k 0 X F L d B H K G f | f C l L J g F X i j h a D G B H k b x 0 E A c K d I e g | g i C K B x X G l D b h k F c L j a f e 0 I J H A d E h | h I J X x k b j H L K A B C e E d c l a i 0 F f g G D i | i c K e G a l h A I d B H k g x J L D C j f 0 F X E b j | j L d g E C D i B c J H A a X G K I b k h F f 0 e x l k | k H I f e l j C J B c K d b F X L A h D a G x E 0 g i l | l J H E F h C b I d A c L j x f B K k i D g e X G 0 a x | x l i H c f G F C k a b j X J K D h g E e d B L I A 0 A | A 0 F b k B K d f E X g x J a D G e H c I i C l h j L B | B f 0 l a H d J F x e X G K C b E g A L c j k D i h I C | C B L 0 X b i a d A I J K D f g c H j l k x E G F e h D | D K A x 0 i k l c J B L I h G F H d a j b X g e E f C E | E b h B I 0 x f a C k D i g d J l j e G X K A c L H F F | F k D I K X 0 e j h i C b E H A a l G f x B L d J c g G | G D j A L F E 0 k a C l h e K d b i X x g J H I c B f H | H F f D C A J K 0 G g e E d k l x X B I L h a b j i c I | I e X a j c H A g 0 G x f B h k F E L J d l i C b D K J | J x E i b K I c G g 0 F X L l h e f d H B k D j C a A K | K G x j l d c L E X f 0 e I D i g F J A H a b h k C B L | L X g k i I B H e F x E 0 A j C f G c d K b h a D l J X | X j k d H G e E D b l i a 0 L I h C F g f c K A B J x
Thus, for example, looking up k in the column to the left, and D in the top row, we find A at their intersection.
This means that "aaba" concatenated with "aabb" forms "aa". This is correct: aaba + aabb = aabaaabb, and eliminating aaa forms aabbb, and eliminating bbb forms aa.
It may be easier to see what is going on with a slightly less compact notation. Except for x and X, if we use only 0, a, b, and A=aa and B=bb as symbols, each element of the group can be represented by a symbol at most three characters long. Here is the table for this group in that form, with the elements in a different order (each element is immediately followed by its inverse instead of the inverses being put in the other half of the table):
| 0 a aa b bb ab BA ba AB aB bA Ba Ab aba bab aBa AbA aBA aBA baB bAB Aba ABa Bab BAb x X
------------------------------------------------------------------------------------------------------------------
0 | 0 a aa b bb ab BA ba AB aB bA Ba Ab aba bab aBa AbA aBA aBA baB bAB Aba ABa Bab BAb x X
a | a aa 0 ab aB Ab aBA aba bb AB abA aBa b Aba BA ABa bA AbA bab BAb x ba Ba bAB X Bab baB
aa | aa 0 a Ab AB b bab Aba aB bb AbA ABa ab ba aBA Ba abA bA BA X Bab aba aBa x baB bAB BAb
b | b ba bA bb 0 bab aa Ba bAB baB BA a aBa AB Bab BAb aB ABa X AbA aba aBA x ab Ab abA Aba
bb | bb Ba BA 0 b Bab bA a aba AbA aa ba BAb bAB ab Ab baB x Aba aB AB X abA bab aBa ABa aBA
ab | ab aba abA aB a BA 0 aBa x BAb aBA aa ABa bb bAB X AB Ba baB bA Aba bab Bab Ab b AbA ba
BA | BA bb Ba BAb aba 0 ab X AbA b baB abA Bab a Aba ba x aa bA aBA bab bAB Ab ABa aB AB aBa
ba | ba bA b bab baB aBa X AB 0 bAB ABa BAb bb aBA aa x BA aB Bab Ab abA Ba a aba Aba ab AbA
AB | AB ABa bab aa Ab x AbA 0 ba abA a Aba baB Bab b ab X bAB aba bb aB BAb bA aBA Ba aBa BA
aB | aB aBa aBA a ab bAB abA aa Aba bA 0 aba X x Ab b BAb Bab ba AB bb baB AbA BA ABa Ba bab
bA | bA b ba aBa bAB bb Bab aBA baB 0 aB x bab Ba X a ABa BA aa Aba ab AB BAb abA AbA aba Ab
Ba | Ba BA bb Bab AbA BAb Aba bAB b aba x Ab 0 X bA abA aa baB ab aBa ABa a ba AB aBA bab aB
Ab | Ab Aba AbA AB aa aBA a ABa Bab X bab 0 Ba aB x baB bb aBa BAb abA ba BA bAB b ab bA aba
aba | aba abA ab BA BAb ABa baB bb a x Ba X aB bab 0 Bab aBA AB bAB b AbA aBa aa Aba ba Ab bA
bab | bab AB ABa baB ba aa b BAb abA Ab X bA x 0 aba Aba bAB a AbA BA aBA Bab ab aBa bb aB Ba
aBa | aBa aBA aB bAB bA X ba x ab Aba Bab b a baB abA AbA 0 BAb Ab ABa Ba aa aba bb bab BA AB
AbA | AbA Ab Aba Ba Bab AB x BA X aa bb bAB aBA ABa BAb 0 aBa bab a aba b aB baB bA abA ba ab
abA | abA ab aba ABa x aB bAB bab BAb a AB Bab BA aBa baB aa Ba aBA 0 ba Ab bb X AbA bA Aba b
aBA | aBA aB aBa X Aba a Ab baB bA ab BAb AbA bAB aa ba aba Bab 0 abA bab BA x b Ba AB bb ABa
baB | baB BAb X ba bab aba ABa bA aBA BA b AB Aba abA aBa bb Ab ab Ba bAB 0 AbA aB aa x a Bab
bAB | bAB x Bab bA aBa abA aB b Ba ABa ba aBA AbA ab bb bab Aba aba AB 0 baB Ab BA X a BAb aa
Aba | Aba AbA Ab aBA X Ba BAb aB aa Bab aBa baB AB BA a bAB bab bb x ab bA ABa 0 ba aba b abA
ABa | ABa bab AB x abA baB aba Bab Ab ba bAB ab aa BAb AbA bA a X b Ba aBa 0 Aba aB BA aBA bb
Bab | Bab bAB x AbA Ba bA bb Ab ABa aBa Aba BA abA b AB aBA aba ba aB aa X ab bab BAb 0 baB a
BAb | BAb X baB aba BA Aba Ba abA bab aBA ab bb ba AbA ABa aB b Ab aBa x a bA AB 0 Bab aa bAB
x | x Bab bAB abA ABa AbA AB ab aBa Ba aba bab bA Ab aB BA ba Aba bb a BAb b aBA baB aa X 0
X | X baB BAb Aba aBA ba aBa AbA BA bab Ab aB aba bA Ba AB ab b ABa Bab aa abA bb a bAB 0 x
The significance of Burnside groups in general is that whether or not all groups of this kind are finite was a mathematical question only recently settled, in a paper by S. I. Adian and P. S. Novikov from 1968, in which it was proven that if, instead of removing any string repeated three times, one removed strings when they were repeated 4381 times, the resulting group would be infinite; and it would also be infinite if any odd number larger than 4381 was used as the criterion.
The Mathieu group M(11), the smallest of the 26 sporadic finite simple groups, (there are, of course, an infinite number of finite simple groups, but most belong to several classes each of which has an infinite number of members) can be represented as the group of the permutations of 11 objects generated by the following two permutations:
1 2 3 4 5 6 7 8 9 10 11 2 3 4 1 5 6 7 9 10 11 8 and 1 2 3 4 5 6 7 8 9 10 11 1 8 7 6 10 4 3 2 9 5 11
It has 7,920 elements.
A particularly beautiful and symmetric set of permutations that yields the 95,040 member group M(12) is given in Numbers, groups, and codes by Humphreys and Prest:
1 2 3 4 5 6 7 8 9 10 11 12 12 11 10 9 8 7 6 5 4 3 2 1 and 1 2 3 4 5 6 7 8 9 10 11 12 1 3 5 7 9 11 12 10 8 6 4 2
Similarly, the 60 element group A(5) can be generated from permutations of 5 objects, as follows:
1 2 3 4 5 5 4 3 2 1 and 1 2 3 4 5 2 3 1 4 5
and a group of 168 members, which is the next non-commutative simple group after A(5), can be generated from these permutations of 7 objects:
1 2 3 4 5 6 7 1 3 4 5 2 6 7 and 1 2 3 4 5 6 7 2 3 1 4 6 7 5
A group provides a set of items, and an operation, similar to addition or XOR, that could be used to apply a keystream to text for purposes of encryption. These days, texts to be encrypted tend to be in binary form.
A group formed from operations on disjoint parts of its elements, such as the group formed by the operation XOR on the individual bits of an 8-bit value, is called an affine group. Obvious groups on strings of bits could be formed by performing XOR on some of their bits and addition on ohter groups of bits. But other possibilities are available; the dihedral groups on polygons of four sides, eight sides and so on are another one.
As it happens, there are many more possibilities than this.
There are 49,487,365,422 distinct (non-isomorphic) groups of order 1,024, and these groups are the overwhelming majority of groups of order below 2,000. For more manageable possibilities, there are 10,494,213 groups of order 512, 56,092 groups of order 256, 2,328 groups of order 128, 267 groups of order 64, 51 groups of order 32, and only 14 groups of order 16 and 5 groups of order 8.
XOR provides the only group of order 2, and XOR and addition provide the only groups of order 4. XOR, addition, and the dihedral group for a quadrilateral provide three of the five possibilities for order 8, and a fourth obvious possibility is provided by the affine group involving adding two of the bits, and XORing the third. The remaining possibility is the quaternion group.
Cyclic Group of Order 8 Dihedral Dih Quaternion Q (modular addition) 8 8 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 1 1 2 3 4 5 6 7 0 1 1 2 3 0 7 4 5 6 1 1 4 3 6 5 0 7 2 2 2 3 4 5 6 7 0 1 2 2 3 0 1 6 7 4 5 2 2 7 4 1 6 3 0 5 3 3 4 5 6 7 0 1 2 3 3 0 1 2 5 6 7 4 3 3 2 5 4 7 5 1 0 4 4 5 6 7 0 1 2 3 4 4 5 6 7 0 1 2 3 4 4 5 6 7 0 1 2 3 5 5 6 7 0 1 2 3 4 5 5 6 7 4 3 0 1 2 5 5 0 7 2 1 4 3 6 6 6 7 0 1 2 3 4 5 6 6 7 4 5 2 3 0 1 6 6 3 0 5 2 7 4 1 7 7 0 1 2 3 4 5 6 7 7 4 5 6 1 2 3 0 7 7 5 1 0 3 2 5 4 Z * Z * Z (XOR) Z * Z 2 2 2 2 4 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 1 1 0 3 2 5 4 7 6 1 1 2 3 0 5 6 7 4 2 2 3 0 1 6 7 4 5 2 2 3 0 1 6 7 4 5 3 3 2 1 0 7 6 5 4 3 3 0 1 2 7 4 5 6 4 4 5 6 7 0 1 2 3 4 4 5 6 7 0 1 2 3 5 5 4 7 6 1 0 3 2 5 5 6 7 4 1 2 3 0 6 6 7 4 5 2 3 0 1 6 6 7 4 5 2 3 0 1 7 7 6 5 4 3 2 1 0 7 7 4 5 6 3 0 1 2
Since data these days is usually transmitted in 8-bit bytes, the groups of order 16 are of more interest. Of the 14 such groups, the ones that either were obvious, or which have become obvious from the list of groups of order 8 above, are:
Z 16 Z * Z * Z * Z 2 2 2 2 Z * Z * Z 2 2 4 Z * Z 2 8 Z * Z 4 4 Dih 16 Z * Dih 2 8 Z * Q 2 8
making eight possibilities. There are six others, and here they are, worked out from their "presentations":
Coding: 0: 1; 1: s; 2: ss; 3: sss; 4: ssss; 5: sssss; 6: ssssss; 7: ssssss; 8: t; 9: ts; a: tss; b: tsss; c: tssss; d: tsssss; e: tssssss; f: tsssssss generalized quaternion s, t; s^8 = 1; t^2 = s^4; sts = t 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 4 5 6 7 0 f 8 9 a b c d e 2 2 3 4 5 6 7 0 1 e f 8 9 a b c d 3 3 4 5 6 7 0 1 2 d e f 8 9 a b c 4 4 5 6 7 0 1 2 3 c d e f 8 9 a b 5 5 6 7 0 1 2 3 4 b c d e f 8 9 a 6 6 7 0 1 2 3 4 5 a b c d e f 8 9 7 7 0 1 2 3 4 5 6 9 a b c d e f 8 8 8 9 a b c d e f 4 5 6 7 0 1 2 3 9 9 a b c d e f 8 3 4 5 6 7 0 1 2 a a b c d e f 8 9 2 3 4 5 6 7 0 1 b b c d e f 8 9 a 1 2 3 4 5 6 7 0 c c d e f 8 9 a b 0 1 2 3 4 5 6 7 d d e f 8 9 a b c 7 0 1 2 3 4 5 6 e e f 8 9 a b c d 6 7 0 1 2 3 4 5 f f 8 9 a b c d e 5 6 7 0 1 2 3 4 Coding: 0: 1; 1: s; 2: ss; 3: sss; 4: t; 5: ts; 6: tss; 7: tsss; 8: tt; 9: tts; a: ttss; b: ttsss; c: ttt; d: ttts; e: tttss; f: tttsss. quasidihedral s, t; s^8 = t^2 = 1, st = ts^3 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 4 5 6 7 0 b c d e f 8 9 a 2 2 3 4 5 6 7 0 1 e f 8 9 a b c d 3 3 4 5 6 7 0 1 2 9 a b c d e f 8 4 4 5 6 7 0 1 2 3 c d e f 8 9 a b 5 5 6 7 0 1 2 3 4 f 8 9 a b c d e 6 6 7 0 1 2 3 4 5 a b c d e f 8 9 7 7 0 1 2 3 4 5 6 d e f 8 9 a b c 8 8 9 a b c d e f 0 1 2 3 4 5 6 7 9 9 a b c d e f 8 3 4 5 6 7 0 1 2 a a b c d e f 8 9 6 7 0 1 2 3 4 5 b b c d e f 8 9 a 1 2 3 4 5 6 7 0 c c d e f 8 9 a b 4 5 6 7 0 1 2 3 d d e f 8 9 a b c 7 0 1 2 3 4 5 6 e e f 8 9 a b c d 2 3 4 5 6 7 0 1 f f 8 9 a b c d e 5 6 7 0 1 2 3 4 modular s, t; s^8 = t^2 = 1, st = ts^5 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 4 5 6 7 0 d e f 8 9 a b c 2 2 3 4 5 6 7 0 1 a b c d e f 8 9 3 3 4 5 6 7 0 1 2 f 8 9 a b c d e 4 4 5 6 7 0 1 2 3 c d e f 8 9 a b 5 5 6 7 0 1 2 3 4 9 a b c d e f 8 6 6 7 0 1 2 3 4 5 e f 8 9 a b c d 7 7 0 1 2 3 4 5 6 b c d e f 8 9 a 8 8 9 a b c d e f 0 1 2 3 4 5 6 7 9 9 a b c d e f 8 5 6 7 0 1 2 3 4 a a b c d e f 8 9 2 3 4 5 6 7 0 1 b b c d e f 8 9 a 7 0 1 2 3 4 5 6 c c d e f 8 9 a b 4 5 6 7 0 1 2 3 d d e f 8 9 a b c 1 2 3 4 5 6 7 0 e e f 8 9 a b c d 6 7 0 1 2 3 4 5 f f 8 9 a b c d e 3 4 5 6 7 0 1 2 G 4,4 s, t; s^4 = t^4 = 1, stst = 1, ts^3 = st^3 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 0 f c d e 9 a b 8 7 4 5 6 2 2 3 0 1 6 7 4 5 a b 8 9 e f c d 3 3 0 1 2 d e f c b 8 9 a 5 6 7 4 4 4 5 6 7 8 9 a b c d e f 0 1 2 3 5 5 6 7 4 3 0 1 2 d e f c b 8 9 a 6 6 7 4 5 a b 8 9 e f c d 2 3 0 1 7 7 4 5 6 1 2 3 0 f c d e 9 a b 8 8 8 9 a b c d e f 0 1 2 3 4 5 6 7 9 9 a b 8 7 4 5 6 1 2 3 0 f c d e a a b 8 9 e f c d 2 3 0 1 6 7 4 5 b b 8 9 a 5 6 7 4 3 0 1 2 d e f c c c d e f 0 1 2 3 4 5 6 7 8 9 a b d d e f c b 8 9 a 5 6 7 4 3 0 1 2 e e f c d 2 3 0 1 6 7 4 5 a b 8 9 f f c d e 9 a b 8 7 4 5 6 1 2 3 0 semidirect product of the cyclic group of order 4 with another copy of itself s, t; s^4 = t^4 = 1, st = ts^3 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 0 7 4 5 6 9 a b 8 f c d e 2 2 3 0 1 6 7 4 5 a b 8 9 e f c d 3 3 0 1 2 5 6 7 4 b 8 9 a d e f c 4 4 5 6 7 8 9 a b c d e f 0 1 2 3 5 5 6 7 4 b 8 9 a d e f c 3 0 1 2 6 6 7 4 5 a b 8 9 e f c d 2 3 0 1 7 7 4 5 6 9 a b 8 f c d e 1 2 3 0 8 8 9 a b c d e f 0 1 2 3 4 5 6 7 9 9 a b 8 f c d e 1 2 3 0 7 4 5 6 a a b 8 9 e f c d 2 3 0 1 6 7 4 5 b b 8 9 a d e f c 3 0 1 2 5 6 7 4 c c d e f 0 1 2 3 4 5 6 7 8 9 a b d d e f c 3 0 1 2 5 6 7 4 b 8 9 a e e f c d 2 3 0 1 6 7 4 5 a b 8 9 f f c d e 1 2 3 0 5 6 7 4 9 a b 8 Coding: 0: 1; 1: a; 2: aa; 3: aaa; 4: b; 5: ba; 6: baa; 7: baaa; 8: c; 9: ca; a: caa; b: caaa; c: cb; d: cba; e: cbaa; f: cbaaa. the group generated by the Pauli matrices a, b, c; a^4 = b^2 = c^2 = 1, cbca^2b = 1, bab = a, cac = a 0 1 2 3 4 5 6 7 8 9 a b c d e f 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 2 3 0 5 6 7 4 9 a b 8 d e f c 2 2 3 0 1 6 7 4 5 a b 8 9 e f c d 3 3 0 1 2 7 4 5 6 b 8 9 a f c d e 4 4 5 6 7 0 1 2 3 e f c d a b 8 9 5 5 6 7 4 1 2 3 0 f c d e b 8 9 a 6 6 7 4 5 2 3 0 1 c d e f 8 9 a b 7 7 4 5 6 3 0 1 2 d e f c 9 a b 8 8 8 9 a b c d e f 0 1 2 3 4 5 6 7 9 9 a b 8 d e f c 1 2 3 0 5 6 7 4 a a b 8 9 e f c d 2 3 0 1 6 7 4 5 b b 8 9 a f c d e 3 0 1 2 7 4 5 6 c c d e f 8 9 a b 6 7 4 5 2 3 0 1 d d e f c 9 a b 8 7 4 5 6 3 0 1 2 e e f c d a b 8 9 4 5 6 7 0 1 2 3 f f c d e b 8 9 a 5 6 7 4 1 2 3 0