The first collectible card game of the modern era, which is also still in active production, is Magic: the Gathering. It was devised by Dr. Richard Garfield, a mathematician, and includes many features that help to provide a challenging and balanced game. For example, most cards require mana to play; mana is normally produced by land cards, only one of which may be played in a turn, and there are five different types (or colors) of mana. Cards which principally require any one of these five colors of mana are inclined to favor different specialized ways of winning the game, and so deck design balances versatility, by using cards which rely on different colors of mana, and having enough mana of the right kind available early enough, by keeping the number of different colors of mana in use to a minimum.
The first Magic: the Gathering cards were printed by Cartamundi, a noted firm in the business of supplying customized playing cards, but Wizards of the Coast later switched to other suppliers. However, it has been claimed that regardless of who printed the cards for Magic: the Gathering, cards for it have always been printed on sheets of 11 cards by 11 cards.
And this page is concerned with the triviality of just how they manage that.
The Fourth Edition of the Core Set of Magic: the Gathering consisted of 5 basic lands with three different versions of artwork each, for a total of 15 cards of this type, 121 cards at the common level of rarity, 121 cards at the uncommon level of rarity, and 121 cards at the rare level of rarity.
So one puts the 121 rare cards on one rare sheet, printing as many of those as desired, the 121 uncommon cards on one uncommon sheet, and the 121 common cards on one common sheet. Finally, 15 times 8 is 120, so we have one unused card left over on the sheet used for printing basic lands.
The Tenth Edition of the Core Set had four different versions of the artwork for the five basic lands, so this time 20 times 6 is 120; it again had 121 cards in each of the three rarity levels. The Ice Age expansion set had the same composition.
As well, the Alpha, Beta, Unlimited and Revised editions of the Core Set also had three sheets of 121 cards with no mixing of rarities of normal cards across sheets.
Revised Edition had 75 commons, 95 uncommons, and 121 rares; the remaining spaces on the common and uncommon sheets contained basic lands. Beta and Unlimited edition contained 75 commons, 95 uncommons, and 117 rares, and so there were also basic lands on the rare sheet. Alpha contained 74 commons, 95 uncommons, and 116 rares, as two cards were omitted due to last-minute errors.
In the early years of Magic: the Gathering, expansion sets, which supplemented the original game, were sold in the form of booster packs which contained only 8 cards, instead of the usual number of 15 cards that has been used both for the Core Set and the later expansions that were organized into blocks.
There were two exceptions to this; Legends was sold in the form of standard 15-card booster packs, and Chronicles was sold in 12-card booster packs.
Also, the second set from the Ice Age block, Alliances, was sold in 12-card booster packs, and also had a limited number of cards with a different rarity due to the number of times they were printed on the sheet.
Instead of the cards having rarities of "rare", "uncommon", and "common", card rarities are often indicated for these sets by codes such as U1, U3, C1 and C3. The letter indicates whether the card was printed on the uncommon sheet or the common sheet, and the number indicates the number of times it occurred there.
In the booster packs with 8 cards, two were from the uncommon sheet, and six from the common sheet; in those for Chronicles, three were from the uncommon sheet, and nine from the common sheet, so in both cases, exactly three times as many copies of the common sheet were printed as of the uncommon sheet.
The distribution of rarities for these sets is:
C11 C6 C5 C4 C3 C2 U4 C1 U3 U2 U1 R1
Arabian Nights 1 9 15 2 1 1 17 33
4 + 51 + 66 = 121
11 + 45+ 60 + 4 + 1 = 121
Antiquities 25 5 11 29 4 26
87 + 8 + 26 = 121
100 + 10 + 11 = 121
Legends 45 30 8 105 121
121 = 121
16+ 105 = 121
90 + 30 = 120
The Dark 40 1 43 35
86 + 35 = 121
120 + 1 = 121
Fallen Empires 15 20 1 25 5 36
75 + 10 + 36 = 121
60 + 60 + 1 = 121
Homelands 50 20 25 45
75 + 45 = 120
100 + 20 = 120
Chronicles 30 7 17 25 46
75 + 46 = 121
90 + 14 + 17 = 121
C3 C2 U6 U2 R6 R2
Alliances 10 40 5 40 3 46
30 + 80 = 110
30 + 80 = 110
18 + 92 = 110
This table is actually somewhat fudged in two places; the numbers for Arabian Nights have been, I hope, corrected, and in the case of Homelands, one card has been moved from U3 to C1 to make things balance.
In any case, based on this history, it seems reasonable to accept the claim that Magic: the Gathering cards were printed on sheets with 121 cards on them, with the Alliances set as one exception. As the Alliances set was the first Magic: the Gathering set of cards printed at a different company instead of Carta Mundi, their original supplier, it makes sense that a different size of sheet might be used, at least initially.
But given that, there really is no reason to suppose that the sets from Mirage block at least through Onslaught block weren't printed on 110-card sheets, if that's the size used by WotC's new supplier.
If Wizards of the Coast's alternate supplier was the U. S. Playing Card Company, it may be of interest to note that, just as Wizards of the Coast, like Parker Brothers, Milton Bradley, Avalon Hill, and Simulations Publications Incorporated (SPI) are now all owned by Hasbro, the U. S. Playing Card Company was taken over by Carta Mundi on the last day of 2019.
Originally known as Russell, Morgan & Company, they began printing their first playing cards in 1881. The name changed to the Russell & Morgan Printing Company in 1885, and then to the United States Printing Company in 1891. Playing card manufacturing was then put in a separate company, the United States Playing Card Company.
Apparently, the return to 121-card sheets took place at the time of Dissension, with the preceding member of Ravnica block, Guildpact, being produced with 110-card sheets. That would coincide with the Ninth Edition of the Core Set being printed on 110-card sheets, and the Tenth Edition being printed again on 121-card sheets.
A typical pack of playing cards contains the normal 52-card deck, two jokers, and one extra card, which might, for example, contain bridge scoring values. This makes 55 cards, for which a 110-card sheet would be highly suited.
In fact, it's so well suited to that, one might well ask what Carta Mundi, the company that made the original Magic: the Gathering cards prior to Alliances, was doing with 121-card sheets. However, this does have a simple explanation. In many European countries, the most common decks of cards might contain simply Ace, 2, 3, 4, 5, 6, 7, Jack, Queen, King or Ace, for a 40-card deck, which could appear three times, with one card left over, on a 121-card sheet, but a 32-card deck, such as Ace, 7, 8, 9, 10, Jack, Queen, King in each suit, or a 36-card deck with Ace, 6, 7, 8, 9, 10, Jack, Queen, King in each suit are even more common.
If the 36-card deck comes with jokers and informational cards, like the 52-card deck usually does, printing it three times on a 121-card sheet would not involve too much waste.
Rather than making a third size of sheet for Tarot card decks, using two different 121-card sheets to print half the deck three times on each would be the simplest solution. Also, decks made for such games as Austrian Tarock have 54 cards in them, the 22 trump cards (including the Fool) and only 32 additional suit cards, Ace, 7, 8, 9, 10, Jack, Queen, King in each suit.
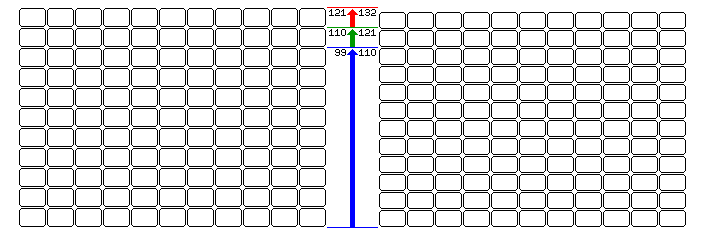
There is a bit more to this than that, though. Playing cards come in different sizes. Magic: the Gathering cards are the same size as Poker-size playing cards, 2 1/2 inches wide and just under 3 1/2 inches tall. There are also Bridge-size playing cards, slightly over 2 1/4 inches wide, and the same height as Poker-size cards. Putting 110 of them on a sheet designed for 110 Poker-size cards would be a level of waste not likely to be tolerated in a large print run.
The ratio of widths is about 9 to 10. So a 110-card sheet for Poker-size cards could be used to print 121 Bridge-size cards, and a 121-card sheet for Poker size cards could be used to print 132 Bridge-size cards, assuming the widths of both types of sheet are the same, and equal 11 card heights plus the necessary spacing between the cards for cutting.
Neither of these sizes is well-suited to printing 55-card decks in Bridge size, so I think it reasonable to suspect that firms which make a lot of such decks will have a third size of sheet, suited to printing 110 Bridge-size cards or 99 Poker-size cards.

And the 40-card deck is usually used in Italy with cards of different sizes entirely; Trevigane style cards are about 1 15/16 inches wide and 4 1/8 inches high, Sicilian style cards are about 2 1/16 inches wide and 3 1/4 inches high. And Tarot cards are often oversized.
Since this was written, I've learned that there is a common specific size of card associated with Tarot cards: 2 3/4 inches wide by 4 3/4 inches high.
Eleven card heights of 3 1/2 inches makes 38 1/2 inches. Two Tarot card widths of 2 3/4 inches is 5 1/2 inches, and two Tarot card heights of 4 3/4 inches is 9 1/2 inches. As 5 1/2 is eleven times 1/2 inch, 38 1/2 inches will be a multiple of it; so seven pairs of Tarot cards will fit across the width of a sheet.
Since 2 1/2 inches is five times 1/2 of an inch, five times 9 1/2 inches would be a multiple of the width of a Poker size card, but as it would be 19 times the width of a Poker size card, this would only avoid wasting cardboard on a sheet size used both for making Poker size cards and for making Tarot size cards if that sheet produced 209 Poker size cards, so it would have to be about twice as large as the sheets that are actually in use.
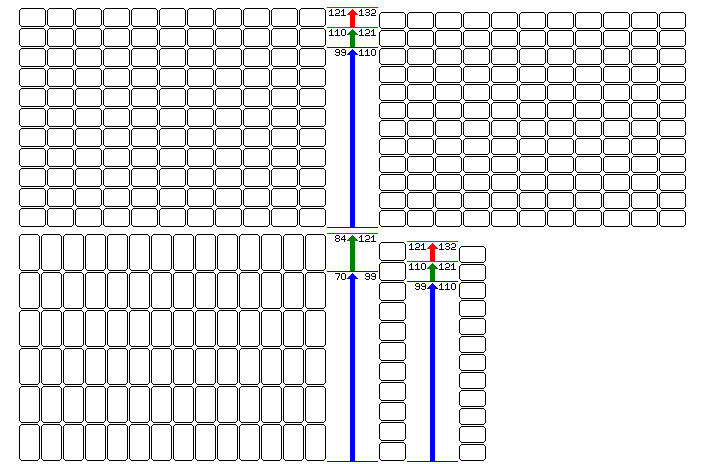
Looking at how the situation would actually work out, a sheet that would have room for 70 Tarot size cards would be larger than one for 110 Bridge size cards, but smaller than one for 110 Poker size cards. One possibility would be for a firm that made playing cards to have presses that could accept sheets for either 110 Bridge size cards or 110 Poker size cards, since 55-card decks in both sizes would be its chief products; and, of course, in that case, adjusting the presses to handle sheets of an intermediate size between the two would likely also be possible.
Printing Tarot decks with sheets of that size would be only a little inconvenient; one sheet could contain 70 of the cards, and a second sheet could contain 10 additional cards, the remaining eight plus two extras, seven times over.
In some cases, it isn't too difficult to figure out how the cards for a Magic: the Gathering expansion might have been printed on 121 card sheets.
The Eventide expansion consisted of 60 commons, 60 uncommons, and 60 rares. Thus, a sheet for each rarity level would have two copies of each card, with only one card wasted. The Future Sight set had a similar structure, with each rarity being divided into 33 normal cards and 27 cards with a different design representing creatures and spells - and card designs - that came from the future.
The Lorwyn and Shadowmoor sets had 121 common cards, 80 uncommons, and 80 rares.
The simplest way to deal with this would have been to have one sheet for the common cards, and two sheets for each of the other two rarity levels, with 40 cards repeated three times. It isn't clear that there is an obvious improvement available.
The Darksteel, Fifth Dawn, Betrayers of Kamigawa, Saviors of Kamigawa, and Guildpact expansions all had 55 commons, 55 uncommons, and 55 rares.
These sets were likely printed when Wizards was having its cards printed by a supplier that used 110-card sheets, and so each rarity would have been printed twice on a sheet.
The Stronghold, Exodus, Urza's Legacy, Urza's Destiny, Nemesis, Prophecy, Planeshift, Apocalypse, and Scourge expansions all consisted of 55 common cards, 44 uncommon cards, and 44 rare cards.
The common cards could each have been printed twice on a common sheet of 110 cards.
If the 44 rare cards are printed once each on the rare sheet, that leaves 66 positions open, on which the correct amount of 22 of the uncommons could each be printed three times.
The remaining 22 uncommons could then be printed five times each on another sheet, of which as many copies could be printed as required.
The expansions Mirrodin, Champions of Kamigawa, and Ravnica all had 20 basic land cards, 110 commons, 88 uncommons, and 88 rares in the set, so they could have been produced by a similar method.
The largest Magic: the Gathering set was the Fifth Edition of the Core Set. It came with 20 basic land cards, 165 commons, 132 uncommons, and 132 rares.
Booster packs in this set had 1 rare, 3 uncommons, 10 commons, and one basic land.
The obvious starting point is to have a rare sheet with 121 of the rares, and an uncommon sheet with 121 of the uncommons.
Let us have an uncommon sheet with the remaining 11 of the uncommons, and a rare sheet with the remaining 11 of the rares.
On the uncommon sheet, if we print 3 copies of 11 of the commons, we can print one copy of these same 11 commons on the rare sheet to have the right amount of those 11 commons. If we only print 2 copies of 11 of the commons, then we will need 4 copies of these same 11 commons on the rare sheet. As it happens, both 3+2 and 1+4 equal 5, and there are 110 cards left on the two sheets.
So on the second rare sheet, we have four copies of 22 of the common cards, and one copy of another 22 of the common cards.
On the second uncommon sheet, we have two copies of the first 22 of the common cards, and three copies each of the other 22 of the common cards.
This takes care of printing as many as are needed of 44 of the common cards, and so when a common sheet is printed with the other 121 commons, a set with 165 commons, 132 uncommons, and 132 rares is achieved.
Could it have been printed on 110-card sheets?
Dealing with the commons would have been simpler: the 165 commons could simply be printed by having one copy each of 110 of them on one sheet, and two copies each of the other 55 on the second sheet.
How do we deal with the rares and the uncommons?
With 110 cards per sheet, we could print sheets with these combinations of cards:
Three copies each of 11 uncommons, and one copy each of 77 rares.
Three copies each of 22 uncommons, and one copy each of 44 rares.
Three copies each of 33 uncommons, and one copy each of 11 rares.
That makes one choice clearly available: print one sheet with 110 of the uncommons. Then, print 11 uncommons eleven times each on one sheet. Print the remaining 11 uncommons three times each with 77 of the rares printed once. Print the final 55 rares twice each on another sheet.
When the Coldsnap expansion, the third member of the Ice Age block, was printed after a lapse of years, it had 60 commons, 55 uncommons, and 40 rares.
I suppose that the 60 commons could have been printed twice over, and the 40 rares printed three times over, on sheets of 121 cards, while the 55 uncommons were printed twice over on a sheet of 110 cards. Assuming, though, that the cards weren't printed in the middle of a change of suppliers like that, how else could this have been handled?
Coldsnap was printed in July 2006, which was shortly after Wizards had apparently returned to a supplier using sheets of 121 cards.
So we can assume the 60 commons were printed twice over on a sheet of 121 cards.
One sheet, of course, could easily print all 40 of the rares three times over.
If we were to print 40 of the uncommons, three times over, on one sheet, then we have 15 uncommons left to deal with.
Printing those 15 uncommons eight times over would fill another sheet, so only one extra sheet is needed to print this unusual number of cards for a 121-card sheet.
The Morningtide expansion had 50 cards of each rarity.
The obvious way to proceed, would be simply to have six sheets, two for each rarity; one with 30 cards repeated four times over, one with 20 cards repeated six times over.
An intermediate solution requires five sheets. Since the number of commons required does not have a simple ratio to the number of rares and uncommons, use two sheets for them, one with 30 cards repeated four times over, one with 20 cards repeated six times over.
The rare sheet can consist of all 50 rares once, with 23 uncommons printed three times over, and two blank spaces.
The number of uncommons remaining is 27; they could be handled with two sheets, one containing 12 uncommons printed ten times over, and one containing 15 uncommons printed eight times over.
Recently, a new rarity level was introduced to Magic: the Gathering, the Mythic Rare. These cards are half as frequent as normal rare cards.
The Conflux and Alara Reborn expansions have 60 commons, 40 uncommons, 35 rares, and 10 mythic rares.
Since a mythic rare is half as frequent as a rare, combining 35 rares printed twice with the 10 mythic rares to produce 80 cards is an obvious way to proceed. One could repeat this three times to fill two sheets of cards. One sheet of cards can handle the 40 uncommons repeated three times, and one can handle the 60 commons repeated three times.
However, there's no need to print an extra sheet of cards. Instead, the rare sheet can contain two copies of each of the 35 rare cards, and one copy of each mythic rare, filling up 80 spaces on that sheet, and then 40 of the remaining 41 spaces can be filled with one copy of each of the 40 uncommon cards.
A small amount of additional uncommons will only mean that slightly fewer copies of the uncommon sheet, with three copies of each uncommon, need to be printed.
The Shards of Alara expansion included 101 common cards, 60 uncommon cards, 53 rare cards, and 15 mythic rares.
60 uncommon cards repeated twice will make a sheet with one card left over.
53 rare cards repeated twice, with 15 mythic rare cards occurring once, fill a sheet of 121 cards exactly.
How does one then handle the 101 common cards?
One way would be to print a sheet with the 101 common cards and the 20 basic lands. This would make about twice as many basic lands as were needed, but they could be stockpiled for use in the two later expansions and in other products.
100 equals 60 plus 40, so if there were only 100 common cards in the set, it would be easy and obvious to see that one could print one sheet with 60 of the common cards repeated twice, and another sheet with 40 of the common cards repeated three times each.
Can we still manage with 101 commons in the set? Both common sheets still have one unused spot left. If the remaining position in both of those sheets was filled with the one left-over common, the result would be that 5/6ths of the required supply of that common would be printed - one half of it from the sheet with two copies each of 60 cards, and one-third from the sheet with three copies each of 40 cards.
But there's also a blank position on the uncommon sheet. Each of the 60 uncommons is repeated twice there, however. So we would have a supply of this remaining common half as large as that of any individual uncommon. Would that supply be sufficient?
Imagine 101 average booster packs. They should contain ten copies of each of the 101 common cards. 60 average booster packs would contain three copies of each of the uncommon cards. So, from the common sheets, we have 5/6ths of the 10 copies of the 101st common card that we need, or 8 1/3 copies. From the uncommon sheets, we will have 101/60 times 1 1/2 copies of the 101st common card. This is more than 2 1/2 copies, so we have plenty without having to also use the unused spot on the rare sheet.
The Visions and Weatherlight expansions each had 62 common cards, 55 uncommon cards, and 50 rare cards. For these early expansion (rather than core) sets, a booster pack contained 1 rare, 3 uncommons, and 11 commons.
To begin, one could have a common sheet with two copies of each of 60 of the 62 common cards, and one blank space; and a rare sheet with two copies each of the 50 rare cards, and six copies each of three of the uncommon cards, leaving three blank spaces.
An uncommon sheet with two copies each of the remaining 52 uncommon cards would have 17 spaces left.
If we added eight copies of one of the remaining common cards to the uncommon sheet, we would have enough of those common cards for booster packs with twelve common cards, so there is enough space to handle both remaining common cards.
Magic: the Gathering, and the names of the expansion sets referenced here, as well as the card names, the mana symbols, and the pentagon of colors, are trademarks of Wizards of the Coast LLC, a subsidiary of Hasbro, Inc..