I remember, shorly after the Challenger disaster, before its cause had become known, watching a television interview with that as its topic.
The interviewer asked the guest if the fact that there was a fatal accident on only the 25th mission did not indicate that the Space Shuttle was unsafe.
The guest being interviewed replied that, no; this was no evidence at all one way or the other. As long as there was some possibility of a mishap, even if the chance were one in a thousand, or one in a million, the accident could have come as easily on the 25th mission as on any other.
That is a true statement, and yet a naïve individual would tend towards the conclusion that, in the absence of other information, it was most reasonable to assume, if the first fatal accident took place on the 25th mission, that the chance of a fatal accident is somewhere around 1/25 to 1/50.
The point of view of such a man in the street is an instinctive and unsophisticated application of something that is referred to as Bayesian statistics. And the validity of Bayesian statistics is subject to controversy.
Classical probability theory dealt with events of which the probability was known. Thus, from symmetry, we can conclude that dice, if they are well-made, have a probability of falling with any one face up that is very near one-sixth.
Or, if we are drawing a ball at random from a bag in which six black balls and thirty-one white balls were placed, the chance of drawing a black ball is 6/37.
We can, for such a case, draw up a table of the possible outcomes when drawing five balls from such a bag, and give a probability to each one.
But what if things are the other way around?
What if someone has prepared a bag with white balls and black balls in it, without telling us how many of each are present, and we draw four balls from it, and two are white and two are black?
We can say that in the absence of other information, as far as we know, it is likely that the proportions of white and black balls in the bag are nearly equal.
But can we actually give a number to how likely it is for the bag to contain numbers of white and black balls that are within a certain range of ratios?
If we had a definite prior probability to work from, there would be no problem.
If, for example, we knew that the bag had exactly fifty balls in it, and it was prepared by flipping a coin fifty times to determine the color of each ball placed in it, then the problem would be straightforward, if complicated. Just calculate for each case what the chance would be of drawing two white balls and two black balls, multiply that chance by the chance that the bag would have been originally prepared with that particular proportion of white and black balls, and one would have the relative proportion for each combination.
But if, instead, the bags were prepared with a strong bias towards more black balls than white balls, then, on the occasions when a draw of four balls turned up two white balls and two black balls, it would still be most likely that the bag had more black balls in it than white.
So Bayesian statistics seems to be based on an assumption about something that we don't know, and, indeed, in the cases where Bayesian statistics are resorted to, something we can't know.
While that is a valid argument that Bayesian statistics is fallacious, the very fact that the prior probability can't be known means that using classical probability instead to deal with the situation is not possible. So we have no choice but to resort to a method which we know is imperfect, providing only approximate answers that we can only hope are likely to be true.
More recently, an even more controversial idea has been proposed.
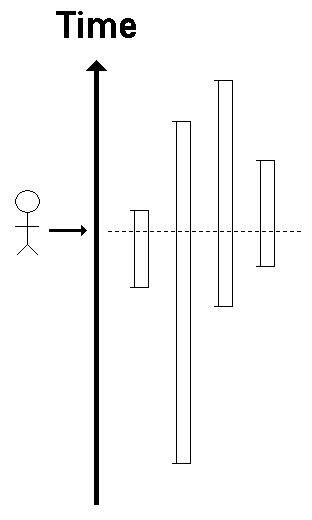
Let us conceptualize reality as this image illustrates:

You, the observer, confront reality at a moment in time, indicated by the horizontal dashed line in the diagram.
You look through the window of your senses, represented by the vertical line, and see various entities... at a random point in the lifespan in each of those entities.
So you would have a 50% chance of seeing any of those entities at some point between one-quarter and three-quarters of its lifspan.
Thus it was that J. Richard Gott III encountered the Berlin Wall in 1968... and predicted that, as it had existed for 7 years, it would likely continue to exist for somewhere between 3 more years and 21 more years. As it happens, it fell in 1989, exactly 21 years later.
Flushed with that success, he published an estimate that human civilization would, with a 95% probability, end somewhere between 12 years and 18,000 years from the present.
This seems to be an attempt to extrapolate from a sample size of zero.
Bayesian statistics has been fairly successful in practice.
But for estimating the probability of a white ball versus a black ball... it's always better to empty the whole bag and count all the balls in it than to simply make an estimate based on past draws.
Similarly, instead of just using how long something has existed, and when we ourselves happened to randomly encounter that thing, as a basis for an estimate of its future life, it's always better to have some actual knowledge of how long such things last.
So while it is valid to say that if we know absolutely nothing else about how long human civilization is likely to last, then the fact that it has existed for about 9,000 years gives it a chance of existing about 9,000 years more, our basis for that vague statement is so weak that we can't say that there is only a 5% chance of civilization lasting more than 18,000 years from now.
We would have to have more solid information on how long civilizations last before we could make such statements.