On the previous page, an attempt at a recurrence relation for three types of rhombs was shown, but it was noted that attempting to make a set of similar rhombs, with the orientation of their sides reversed, ended in failure.
If no attempt is made to take the smaller round shape, the one with sevenfold symmetry, and slice it into parts with odd numbers of fourteenths, can recurrences then be made for the alternate colors of rhombs?
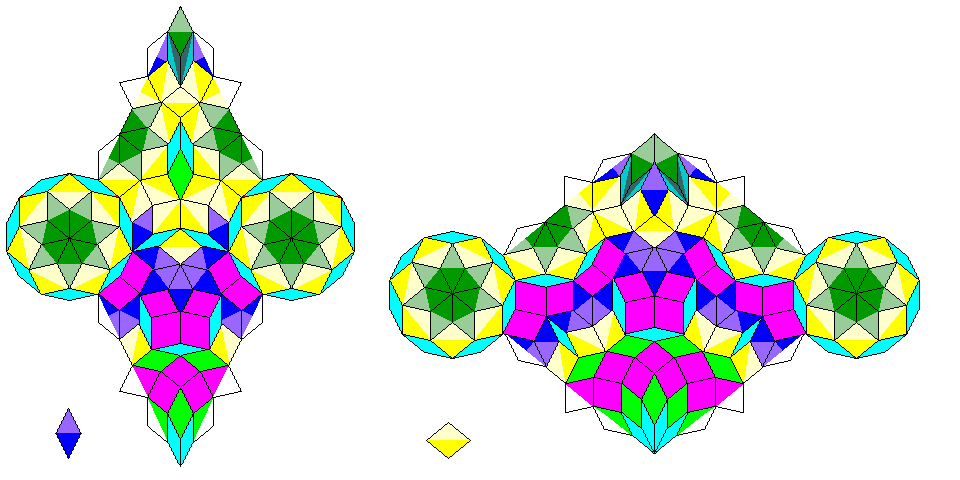
An attempt to do so produces rhombs which are like the desired purple and blue-green rhombs on one side, but which have the colors of their component rhombs inverted on the other side. This means that some changes are required to the way the previously-proposed parts of this recurrence would work.
The small circle shape has to be changed to retain its symmetry. Fortunately, it is not necessary to make an alternate color thin rhomb, because it appears to be impossible to do so:
but we do need a fully color-reversed form of one of the original rhombs for the small circle. Since color reversal seems to be easy enough to achieve, simply with the need to move the thin rhombs around, there are grounds for optimism. Also, while the small circle simply needs to be rotated by one-fourteenth of 360 degrees to become its color-reversed form, the diagrams above show that the large circle becomes changed to a different pattern, shown on the bottom left of the illustration above; this one requires a color-reversed form of the thin rhomb as well.
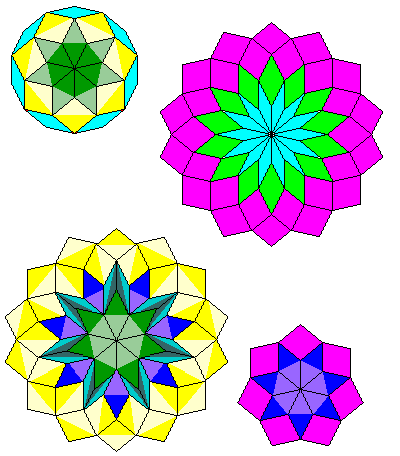
A fourth vertex type is shown, which will be required by the three color-reversed rhombs for which the color-reversed sides of the two alternate color rhombs create the need. Of the four vertex types, one has tetradecagonal symmetry, and the other three have heptagonal symmetry; those three may occur in the alternate orientation obtained, for example, by turning them upside down equally well, and the overall tiling will be found to have fourteenfold or tetradecagonal symmetry.
The original recurrence relations can be changed easily enough to incorporate the color reversals needed for the yellow and blue rhombs:
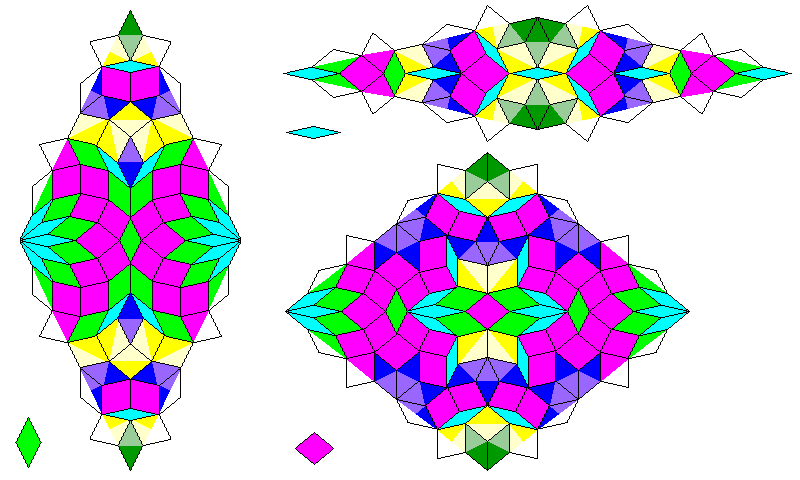
Much more easily, in fact; here, only the color-reversed form of the green rhomb is required, and that only for the seven-pointed stars in the small circle; in the alternate color rhombs, all three color-reversed rhombs were required. An additional modification was performed so that the recurrence would create groups of rhombs with local sevenfold symmetry a few additional times. Will it be possible to perform all the required color reversals?
It seems like it may be impossible, because a color reversed rhomb involves interchanging normal and alternate-color versions of each component rhomb. And there is no alternate-color form of the thin, blue-green, rhomb. In most cases, this could be solved by moving the thin rhombs to the opposite sice of two adjoining rhombs, but the rhombs in the horizontal line bisecting each rhomb seem to be a more difficult case.
But just as the alternate-color rhombs were made possible by recognizing that the small fourteen-sided figure, of which an odd part would be included in the figure, had to be treated separately, this would apply to the completely different pattern which replaces the large fourteen-sided figure.
That pattern, though, has only seven-way symmetry instead of fourteen-way symmetry. However, the placement of the color-reversed rhombs is such that if they also undergo a transformation from one side to the other similar to that of the alternate-color rhombs, as is illustrated in the diagrams above, they will still match up, but a color-reversed thin rhomb is absolutely needed.
And, indeed, here are the three color-reversed rhombs:
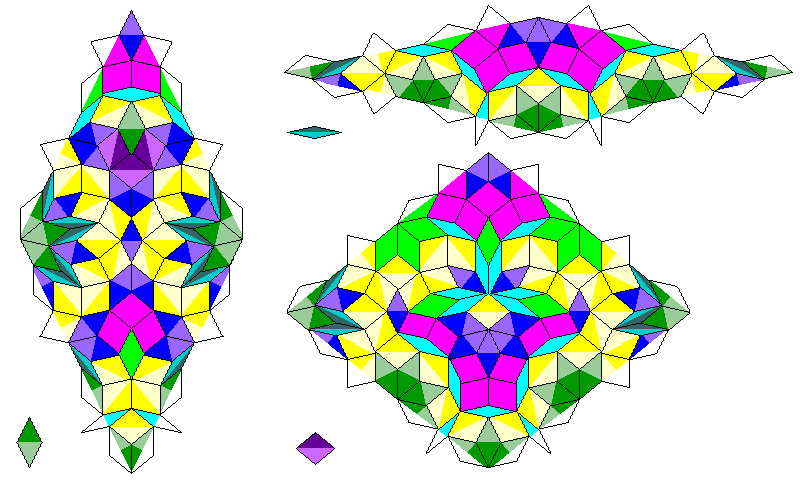
and so, a complete recurrence is obtained which resembles the quasicrystalline rhomb tiling in form.
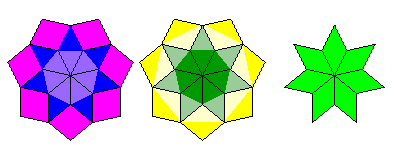
Note that when the two adjacent dark purple sides of a dark purple/grayish purple thick rhomb are in contact, in the middle of a side, not at a vertex, a seven-pointed star made out of seven green rhombs occurs, a locally sevenfold-symmetric figure not occuring at a vertex. The figures at every vertex are locally sevenfold symmetric at least, and occasionally a locally sevenfold symmetric figure also occurs along an edge between vertices: the design has been chosen to force the occurrence of such figures as often as possible.
The three figures with sevenfold symmetry that may occur on the edge between two vertices are:
The first one is the most common, and it also occurs at vertices as well. The second one is somewhat rarer; it is a part of a figure that occurs at a vertex, but when it occurs between vertices, it cannot be completely surrounded by thin rhombs. The third one is the rarest, never occuring at a vertex, and only occurring when two grayish purple halves of a reversed-color thick rhomb come into contact; this happens in the recurrence of the dark green/grayish green reversed-color intermediate rhomb only, the only place where a reversed color thick rhomb is necessary, the other two reversed-color rhombs becoming necessary when producing the recurrences for the alternate color rhombs.
But since writing this, I noticed that the design for the recurrence of the dark green/grayish green rhomb could be improved, eliminating the need for the dark purple/grayish purple rhomb, making for a set of only seven rhombs. But does this mean that the green star is lost?
No; the improvement in the top half of the design which eliminates the need for the eighth type of tile creates a symmetrical seven-pointed star in the middle of the tile, and the same change can be carried out in the bottom of the tile, making the green star both considerably more frequent in the design, and, since it is now surrounded by seven yellow/light yellow alternate color rhombs, increasing the size of that particular type of sevenfold-symmetric area in the design, and, by increasing the number of sevenfold-symmetric stars present, adding further to the amount of explicit sevenfold symmetry occurring.
The tiles observe the following matching rules:
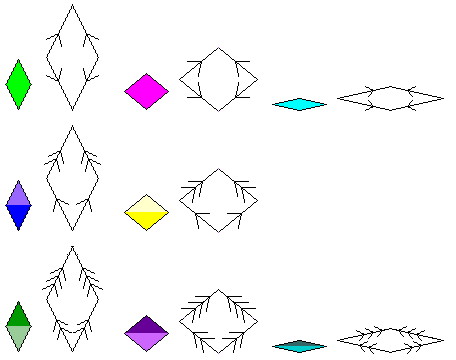
As with the matching rules of the binary tilings, these matching rules are not sufficient in themselves to enforce nonperiodicity, for which the recurrence relations are required.
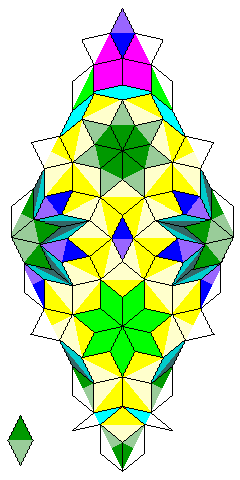
And here is a small likeness of an example of what this tiling looks like beyond the confines of the recurrence for a single rhomb:

Note that the recurrence for the dark green/grayish green rhomb is never reached in this image, so it is unaffected by the change noted above.
A further change is possible, in that one of the vertex types can be replaced by alternate forms, and these forms place the green star at the vertex.

This greatly reduces the need for the reversed-color version of the thin rhomb, but does not eliminate it completely, and, unfortunately, it does not appear that a modification of the recurrence relation for the dark green/grayish green rhomb can be achieved that gets rid of the remaining requirement for that shape.