Most of us are familiar with the ordinary trigonometric functions, such as the sine, the cosine, and the tangent.
Where e is the base of the natural logarithms, approximately 2.71828... , analogous functions, referred to as the hyperbolic trig functions exist that are defined as:
Hyperbolic sine:
x -x
e - e
sinh(x) = ----------
2
Hyperbolic cosine:
x -x
e + e
cosh(x) = ----------
2
Hyperbolic tangent:
x -x
e - e
tanh(x) = ----------
x -x
e + e
and analogs of the other trigonometric functions can be derived from them:
Hyperbolic cosecant: csch(x) = 1/sinh(x) Hyperbolic secant: sech(x) = 1/cosh(x) Hyperbolic cotangent: coth(x) = 1/tanh(x)
I had heard this much, but not much else, about them in the course of my education.
Having encountered slide rules with scales indicating the hyperbolic trig functions, I was driven to the conclusion that those functions must be useful for something, and, indeed, that apparently this is particularly the case in respect of electronics, and from their name, presumably they have something to do with a hyperbola, but I really hadn't known what.
Also, I had heard of the unusual function known as the Gudermannian, which links the trigonometric functions and the hyperbolic functions together in a surprising way.

Well, my curiosity finally drove me to look for more information about these functions.
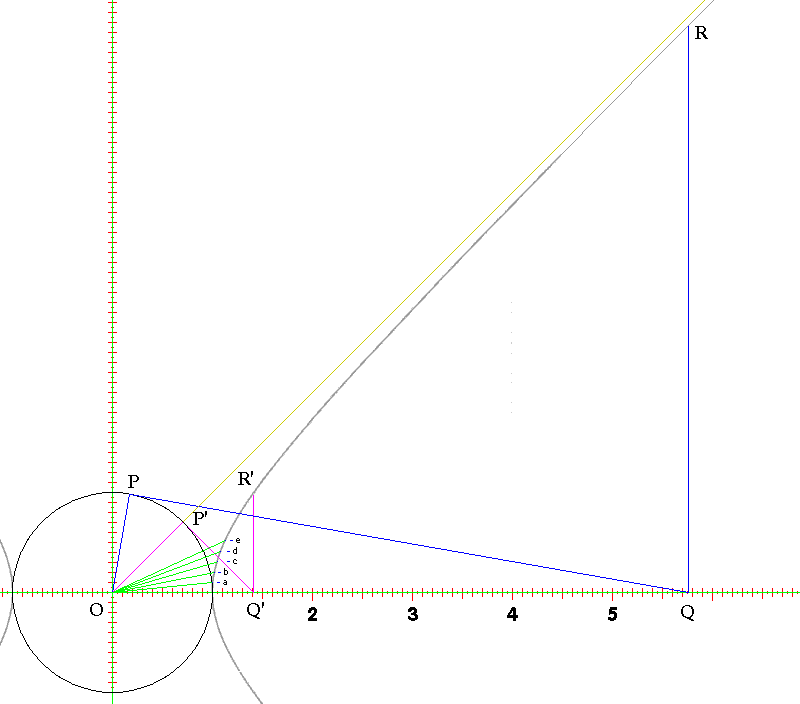
The diagram above shows a unit circle, centered about the point marked O.
A horizontal green line with red tick marks represents the x axis, along which are marked the integers 2 through 5 to indicate its scale. A similar vertical green line with red tick marks represents the y axis.
This diagram is also a graph, and on this graph, the equation of the unit circle is:
2 2 x + y = 1
For an angle theta at the origin, measured from the x-axis, the point on the unit circle has the sine of theta as its y-coordinate, and the cosine of theta as its x-coordinate.
One thing this implies is that the sine and cosine functions have the property
2 2
sin (theta) + cos (theta) = 1
given that the sine and cosine of an angle locate a point on the unit circle, then those values must satisfy the equation of the unit circle; and the equation of the unit circle is what it is because the Pythagorean theorem happens to be true.
Touching the unit circle at the points (x,y)=(1,0) and (x,y)=(-1,0) are two curved lines which bend outwards from it. Those lines form the hyperbola with the equation
2 2 x - y = 1
and it is this hyperbola, which we may term the unit hyperbola, that is connected to the hyperbolic trig functions.
The points (x,y)=(cosh(u),sinh(u)) for u equal to 0.1, 0.2, 0.3, 0.4, and 0.5 are marked on the graph with a, b, c, d, and e as their labels, and green lines are drawn to them from the point O or (0,0).
The value of u corresponds to both the area bounded by the x-axis on the bottom, the hyperbola to the right, and the line from O to (cosh(u),sinh(u)) on the top, and to the integral of the ratio of the current increment of distance along the hyperbola from the x-axis to the distance of that point on the hyperbola from the origin.
So, with the hyperbola and the hyperbolic trig functions, as with the circle and the ordinary trig functions, the sine is a vertical co-ordinate, and the cosine is a horizontal co-ordinate.
And just as the sine and the cosine satisfy the equation of the circle, the hyperbolic sine and cosine satisfy the equation of the hyperbola, and so:
2 2
cosh (u) - sinh (u) = 1
Now we come to the curious geometrical construction involving the points O, P, Q, and R, or O, P', Q', and R', on the diagram.
The line from O to P' makes a 45 degree angle with the x-axis, and the line from O to P makes an 80 degree angle with the x-axis.
Thus, the point P' is (x,y)=(cos(45°),sin(45°)) and the point P is (x,y)=(cos(80°),sin(80°)).
The points R' and R happen to be on the hyperbola, which means that the point R' must be (x,y)=(cosh(u),sinh(u)) and the point R must be (x,y)=(cosh(v),sinh(v)) for some u and v.
Let us now think of a general point of the same type on the unit circle, the point P'', which is (x,y)=(cos(theta),sin(theta)) for some angle theta.
When we take the tangent to the circle at the point P'', and follow it to the x-axis to find the point Q'', where is that point?
Given that the angle between O and Q'' at P'' is a right angle, it is evident enough: the distance of Q'' from the origin is 1/cos(theta).
From the equation of the hyperbola, therefore, we know that point R'' must be the point
/ _______________________ \
| / 2 |
| 1 / / 1 \ |
(x,y) = | ------------ / | ------------ | - 1 |
| cos(theta) , \/ \ cos(theta) / |
\ /
And since we also know that, since R'' is on the hyperbola, and on the part of the hyperbola in the quadrant where x and y are both positive, it must also be the point
(x,y) = ( cosh(w), sinh(w) )
for some w,
we can think of this geometric construction as creating a relationship between w and theta. And, indeed, it's clear enough that cosh(w) = 1/cos(theta).
As it happens, 1/cos(theta) is also known as sec(theta), the secant of the angle theta. And there is a relation involving the square of the secant:
2 2
sec (theta) - tan (theta) = 1
for any theta.
How can this be?
Well, if we multiply everything by cos(theta) squared, we get:
2 2
1 - sin (theta) = cos (theta)
our old friend from the equation of the circle. So the fact that the circle relates the sine and the cosine implies that the secant and the tangent are related by the hyperbola.
Therefore, our point R'' happens to be
(x,y) = ( sec(theta), tan(theta) ) = ( cosh(w), sinh(w) )
which is where the remarkable identity
-1 -1
cosh (sec(theta)) = sinh (tan(theta))
comes from, since w is equal to itself. Or one can also invert this, to give two definitions for theta in terms of w, since theta is also equal to itself:
-1 -1
sec (cosh(w)) = tan (sinh(w))
and theta is the Gudermannian of w.
Since the x and y coordinates of R'' in both forms are equal, one can also obtain the equation
tan(theta) sinh(w) ------------ = --------- sec(theta) cosh(w)
which becomes
sin(theta) = tanh(w)
and so we have three ways to express the Gudermannian:
-1 -1 -1
gd(w) = theta = sin (tanh(w)) = sec (cosh(w)) = tan (sinh(w))
which can be increased to six by taking the reciprocals on both sides of the equations:
-1 -1 -1
gd(w) = theta = csc (coth(w)) = cos (sech(w)) = cot (csch(w))
From these six formulas, of course, we can obviously derive six formulas for the inverse of the Gudermannian. But there is also a seventh one:
-1 pi theta
gd (theta) = w = ln ( tan ( ---- + ------- ) )
4 2
Pi/4 radians is, of course, 45°.
Using complex numbers, another close relationship between the conventional trigonometric functions and the hyperbolic trig functions of a more trivial nature can be found.
Since
2 3 4 5 6 7 8 9 10 11 12
x x x x x x x x x x x x
e = 1 + x + -- + -- + -- + -- + -- + -- + -- + -- + --- + --- + --- + ...
2! 3! 4! 5! 6! 7! 8! 9! 10! 11! 12!
and
3 5 7 9 11 13
x x x x x x
sin(x) = x - -- + -- - -- + -- - --- + --- - ...
3! 5! 7! 9! 11! 13!
and
2 4 6 8 10 12
x x x x x x
cos(x) = 1 - -- + -- - -- + -- - --- + --- - ...
2! 4! 6! 8! 10! 12!
one can obtain, given that e^(a+b) = e^a * e^b for all a and b, even if a and b are complex numbers, the formula
(x + iy) x e = e ( cos(y) + i sin(y) )
which lets us conveniently express e, raised to a complex number, in terms of e raised to a real number, and the ordinary sine and cosine functions of real numbers.
Plugging this definition of e raised to a complex power into the definitions of the hyperbolic trig functions in terms of e^x given above, one can easily obtain the identities
sin(z) = -i sinh(iz) sinh(z) = i sin(-iz) = -i sin(iz) cos(z) = cosh(iz) cosh(z) = cos(-iz) = cos(iz) tan(z) = -i tanh(iz) tanh(z) = i tan(-iz) = -i tan(iz) cot(z) = i coth(iz) coth(z) = -i cot(-iz) = i cot(iz)
also making use of the fact that the cosine is an odd function, while sine, tangent, and cotangent are all even functions.
But perhaps the most important relationship between the trigonometric functions and the hyperbolic functions involving complex numbers is contained in these equations:
sin(x+iy) = ( sin(x) * cosh(y) ) + i * ( cos(x) * sinh(y) ) cos(x+iy) = ( cos(x) * cosh(y) ) + i * ( sin(x) * sinh(y) ) sinh(x+iy) = ( sinh(x) * cos(y) ) + i * ( cosh(x) * sin(y) ) cosh(x+iy) = ( cosh(x) * cos(y) ) + i * ( sinh(x) * sin(y) )
This makes it easy to see why slide rules with scales for the hyperbolic functions were called vector slide rules. With scales for the hyperbolic functions, it is possible to quickly calculate trig functions of complex numbers.