Here, we are examining the identity
i * pi e = -1
The reason I do not consider this equation to be as profound as is sometimes claimed is because that first equation is really a disguised way of saying that the cosine of 180 degrees is equal to minus one. But to understand why that is, it is necessary to understand a fair amount of mathematics.
Let us start by reviewing the log and trig functions.
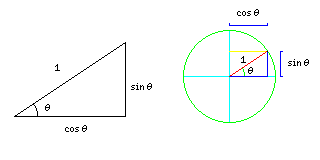
The trigonometric functions are usually presented in relation to the sides of a right triangle. If the hypoteneuse (the long side opposite the right angle) of the triangle is one unit in length, then the other side opposite an angle is the sine of that angle in length, and the other side touching that angle is the cosine of that angle in length.

As the diagram above shows, we can also think of the sine and cosine of an angle to be the vertical and horizontal coordinates of a point on the circumference of a circle of unit radius. This makes it clearer what we mean when we speak of the sine and cosine of negative angles, or angles larger than 90 degrees.
On a computer, if you ask for SIN(30), instead of getting .5 as an answer, you might get -0.9880316 as your answer. To get the answer of .5, you need to ask for SIN(0.5235988) instead, where 0.5235988 is equal to pi (3.14159 26535 89793...) divided by 6.
This is because, in mathematics, as opposed to the everyday arithmetic which might be used, in, say, carpentry, angles are typically measured in units called radians. Why? What is special about radians?
As you know, the circumference of a circle is equal to pi times its diameter. Therefore, the circumference of a circle is also equal to two times pi times its radius.
Thus, as illustrated below:
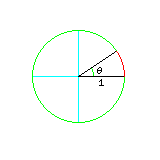
the length of the arc subtended by an angle theta is the same fraction of the circumference of the circle, which, for a circle with radius equal to 1 (called a unit circle), is two times pi, as the angle theta is a fraction of 360 degrees. So, if we instead use radians as our unit of angle, where 180 degrees equals pi radians, and so 360 degrees equals two times pi radians, our angle in radians is the same as the length of that arc.
Thus, the sine of the angle theta can now be thought of as the length of a straight line which touches the end of a curved arc of length theta.

When you cut a thin wedge of pie, the shape of that wedge is almost the same as that of a narrow isosceles triangle. The fact that the back of the slice is curved becomes less and less important as the wedge gets thinner. So, as 2 times theta tends to zero, sin( theta ) and theta, where theta is measured in radians, get closer to being equal. (The diagram above shows how an isosceles triangle with an angle of 2 times theta at its point is the same as two right triangles with an angle of theta back to back, forming a symmetrical shape which is easier to compare with a wedge taken from a circle than a right triangle by itself is.)
Thus, the limit of sin(x)/x as x tends to zero is one, when x is measured in radians. Because that means that sin(x) for small x just about equals x, that also means that when x is in radians, the formulas used to calculate sin(x) as a function of x take their simplest, and hence most natural, form. This is why mathematicians prefer radians. Connected with this is the fact that when x is in radians, formulas in calculus about sin(x) are simpler.
In differential calculus, mathematicians (and, indeed, more humble users of mathematics) calculate, for a function of x (call it f(x)), what the rate of change in the value of that function is at any x. That rate of change, sometimes noted as f'(x), is the limit, as d goes to zero, of (f(x+d)-f(x))/d. That is,
df f(x+d) - f(x)
f'(x) = -- = lim -------------
dx d->0 (x+d) - (x)
where df/dx is another notation for f'(x). Note that f(x+d) - f(x) is the change in f(x), sometimes noted as delta f, and d, which is (x+d) - x, is the change in x, sometimes noted as delta x. Thus, df/dx is the limit, as the step size goes to zero, of delta f/delta x, which is the reason for that particular notation (due to Leibnitz).
Some common derivatives can be worked out by simple algebra.
If f is the function defined by f(z)=1 for any z, then f'(x) is zero, since f(x+d) and f(x) are always both 1, whatever x and d might be.
If f is defined by f(z)=z, then what is f'(x)? The answer is that f'(x)=1, since f'(x) is the limit of ((x+d)-x)/((x+d)-x) as d goes to zero. While that is 0/0 when d is zero, for every other value of d, it equals d/d which is 1, and the limit of a function for a value is concerned with what number the function gets close to as the parameter gets close to the target, not with what happens when it actually gets there.
If f is defined by f(z)=z^2, then what is f'(x)? Here, f'(x) is the limit of ((x+d)^2-x^2)/d as d goes to zero. This is ((x^2+2xd+d^2)-x^2)/d, which is (2xd+d^2)/d, or 2x+d. The limit of this, as d goes to zero, is 2x.
Similarly, for f(z)=z^n in general, f'(x)=n(x^(n-1)). Also, as is fairly obvious, if f(z)=k*g(z), then f'(x)=k*g'(x), and if f(z)=g(z)+h(z), then f'(x)=g'(x)+h'(x).
If f(z)=sin(z), where z is in radians, what can we say about f'(x)? As it turns out, sin'(x)=cos(x), and cos'(x)=-sin(x). Basically, the reason for this is the following fact: as you walk around in circles counterclockwise, the direction in which you are facing is always 90 degrees counterclockwise from the direction of your separation from the center of the circle.
As we know, sin(x) is approximately equal to x when x is small. Thus, sin'(0)=1; this makes sense, because cos(0)=1.
Given that for f(z)=z^n, it is true that f'(x)=n(x^(n-1)), we can work out a way to approximate a function if we know all its derivatives at one point. This is true for sin(x), since sin'(x)=cos(x), sin''(x)=cos'(x)=-sin(x), sin'''(x)=cos''(x)=-sin'(x)=-cos(x), and on and on going through sin(x), cos(x), -sin(x) and -cos(x) in order over and over again.
Let F(z) be defined as a + bz + c(z^2) + d(z^3) + e(z^4) + f(z^5) + g(z^6) ... and let us also ignore the fact that there are only 26 letters of the alphabet, and that z is one of them. Note also that here f(z^5) is a number f times z^5, and not a function f of z^5. Mathematicians do this kind of thing all the time, and they expect people to not get confused.
Then, F(0) = a.
Since F'(z) = b + 2cz + 3d(z^2) + 4e(z^3) + 5f(z^4) + 6g(z^5) + ..., then F'(0) = b.
Since F''(z) = 2c + 6dz + 12e(z^2) + 20f(z^3) + 30g(z^4) + ..., then F''(0) = 2c.
Since F'''(z) = 6d + 24ez + 60f(z^2) + 120g(z^3) + ..., then F'''(0) = 6d.
Since F''''(z) = 24e + 120fz + 360g(z^2) + ..., then F''''(0) = 24e.
Since F'''''(z) = 120f + 720gz + ..., then F'''''(0) = 120f.
Since, therefore, the n-th derivative of the function F at zero is a multiple of one of the coefficients of this power series for F in z, we can work backwards from the derivatives to find the power series. A power series constructed in this way is called the Taylor series for the function F.
From the above, we can see that the formula for a Taylor series is:
F''(0) F'''(0) F''''(0)
F(z) = F(0) + F'(0)*z + ------ *(z^2) + ------- * (z^3) + -------- * (z^4) + ...
2 2*3 2*3*4
and if we use what we know about the derivatives of sin(x), we get the formula
3 5 7 9 11 13
x x x x x x
sin(x) = x - -- + -- - -- + -- - --- + --- - ...
3! 5! 7! 9! 11! 13!
and similarly, if we move one step ahead in the cycle, and do the same thing for cos(x), we get the formula
2 4 6 8 10 12
x x x x x x
cos(x) = 1 - -- + -- - -- + -- - --- + --- - ...
2! 4! 6! 8! 10! 12!
where n! is a way of writing 1 * 2 * 3 * 4 * ... * (n-1) * n.
Just as SIN(30) didn't give you the expected answer on a computer, it is also true that LOG(10) may return 2.302585 instead of 1, as you might expect. Instead, it is LOG(2.718282) that is 1.
Logarithms were originally used as a way to help people multiply numbers. As long as you only needed the answer to a limited precision, you could use a table to convert numbers to their logarithms and then back again, and this would make multiplication easier, because adding the logarithms of two numbers is the same as multiplying the numbers themselves.
Why is this?
1*1=1. 10*10=100. 10*100=1000. 100*100=10000. 10*1000=10000.
In all these cases, multiplying the two numbers has the same effect as adding the number of zeroes at the end of them, because all these numbers are pure powers of ten. (10*10*10)*(10*10*10*10*10)=10*10*10*10*10*10*10*10, just as 3+5=8, or (1+1+1)+(1+1+1+1+1)=1+1+1+1+1+1+1+1.
Logarithms allow us to multiply by means of addition even for numbers that are not exact powers of ten. One crude way to construct a table of logarithms is just to multiply a number only very slightly greater than 1 by itself over and over:
Log Number 0 1 1 1.0001 2 1.00020001 3 1.000300030001 ...
Then, such a table can be made more useful by estimating in-between values: thus, instead of 1.000300030001, we might want the logarithm of 1.0003, which ought to be about 2.9997.
It can be made still more useful by scaling the logarithms, multiplying them all by a constant factor, so that the logarithm of 10 equals 1. This produces what are known as common logarithms. In that system, the logarithm of 10 is 1, and the logarithm of 2 is .30103... . Since multiplying two numbers is the same as adding their logarithms, the logarithm of 20 is 1.30103... . In general, the integer part of the common logarithm of a number shows where the decimal point is, and the fractional part shows what digits the number is composed of. Thus, the fractional part of a common logarithm is the part that is most helpful in performing multiplication and it is called the mantissa of the common logarithm.
This is why, if a computer represents the real number 2.35 * 10^43 in an internal floating-point format as 43 235000, the 235000 part is called the "mantissa" of the floating-point number. While this is not strictly correct, it is true that the information stored in that part of the floating-point number is the same as the information contained in the mantissa of its logarithm is. If exponents are powers of two in a computer, then the "mantissa" of the floating-point number contains the same information as the fractional part of the logarithm of that number to the base 2.
Why does the LOG function on a computer usually give the logarithm to the base 2.71828...? This number is known as e, the base of the natural logarithms.
This number happens to be:
1 n
e = lim ( 1 + --- )
n->infinity n
Thus, (1.1)^10 = 2.59374... and (1.01)^100 = 2.70481... .
That means that the logarithm of 1.01 to the base e is a bit less than 1/100, since 1.01 to the 100th power is less than 2.71828... . Thus, if f(z)=ln(z), (where ln stands for natural logarithm) then the limit of f'(x), as x approaches 1, is 1.
This also means that if f(z)=e^z, then the limit of f'(z), as z approaches zero, is 1 as well, and thus both the logarithm and its inverse function are in their simplest forms with e as the base.
As it happens, if f(z)=e^z, then f'(z)=e^z as well. Why is this?
Given the definition of e, e^(0.05) is approximately 1.01*1.01*1.01*1.01*1.01. And e^(0.06) is approximately 1.01*1.01*1.01*1.01*1.01*1.01. Thus, e^(0.06) minus e^(0.05) is (1.01^5)*1.01 - (1.01^5), so the difference is (1.01^5)*.01.
In general, since e^(x+d)=(e^x)*(e^d), then the limit as d goes to zero of (e^(x+d)-e^x)/d as d goes to zero is that of ((e^x)*(e^d-1))/d, which is (e^x) times the limit of (e^d-1)/d as d goes to zero, which we previously saw was equal to one because of the choice of e as our base.
Knowing this about the derivatives of f(z)=e^z, the Taylor series for e^x has the form:
2 3 4 5 6 7 8 9 10 11 12
x x x x x x x x x x x
e^x = 1 + x + -- + -- + -- + -- + -- + -- + -- + -- + --- + --- + --- + ...
2! 3! 4! 5! 6! 7! 8! 9! 10! 11! 12!
Now, then, returning to the formula
i * pi e = -1
having a power series for e^x, we are finally able to assign a meaning to e raised to an imaginary power, without trying to multiply a number by itself an imaginary (and fractional) number of times.
i is a number which, when squared, yields -1 as the result. Any positive or negative number, if squared, gives a positive result. This means that imaginary numbers are not the same as ordinary numbers, but they still have many of the same properties as ordinary numbers. A complex number is the sum of a real number (zero, or any positive or negative number, including fractions and irrational numbers) and an imaginary number (a positive or negative multiple of i, the square root of minus one). Thus, while ordinary real numbers can be thought of as positions along a line, complex numbers are a two-dimensional number system. They are very important in analysis, the branch of mathematics that includes calculus, because they reveal the real underlying structure of mathematical functions, such as sine and cosine, or e^x.
Using the Taylor series for e^x, if x=i*z, what is e^(i*z)?
As it turns out, substituting in i*z for x, what we get is:
2 3 4 5 6 7 8 9 10
z z z z z z z z z
e^(i*z) = 1 + iz - -- - i-- + -- + i-- - -- - i-- + -- + i-- - --- - ...
2! 3! 4! 5! 6! 7! 8! 9! 10!
and by comparing our Taylor series for sin(x) and cos(x) above, what we find, therefore, is that:
e^(i*z) = cos(z)+i*sin(z)
Since those series were for cos(z) and sin(z) where z is in radians, that means that e^(i*pi) is equal to cos(180 degrees) plus i times sin(180 degrees), which is -1 plus i times zero. So e^(i*pi) equals -1.