The moments of the Riemann zeta function are said to be linked to the number of Young tableaux. I will not attempt to explain this here, but I can explain what a Young tableau is; for example, a 3x3 Young tableau is a square 3x3 matrix containing the numbers from 1 to 9 such that the numbers in both the rows, as one goes to the right, and the columns, as one goes downwards, are steadily increasing.
Here are the 3x3 Young tableaux:
1 2 3 1 4 7 1 3 6 1 2 4
4 5 6 2 5 8 2 5 8 3 5 7
7 8 9 3 6 9 4 7 9 6 8 9
1 3 5 1 3 6 1 3 4 1 3 5 1 3 4
2 6 8 2 4 8 2 6 8 2 4 8 2 5 8
4 7 9 5 7 9 5 7 9 6 7 9 6 7 9
1 3 6 1 3 5 1 3 6 1 3 4 1 3 5 1 3 4
2 5 7 2 6 7 2 4 7 2 6 7 2 4 7 2 5 7
4 8 9 4 8 9 5 8 9 5 8 9 6 8 9 6 8 9
1 2 6 1 2 5 1 2 6 1 2 4 1 2 5 1 2 4
3 5 8 3 6 8 3 4 8 3 6 8 3 4 8 3 5 8
4 7 9 4 7 9 5 7 9 5 7 9 6 7 9 6 7 9
1 2 6 1 2 5 1 2 6 1 2 4 1 2 5
3 5 7 3 6 7 3 4 7 3 6 7 3 4 7
4 8 9 4 8 9 5 8 9 5 8 9 6 8 9
1 2 3 1 2 3 1 4 5 1 4 5
4 6 7 4 6 8 2 6 7 2 6 8
5 8 9 5 7 9 3 8 9 3 7 9
1 2 5 1 3 5 1 2 7 1 3 7
3 4 6 2 4 6 3 4 8 2 4 8
7 8 9 7 8 9 5 6 9 5 6 9
1 2 3 1 2 3 1 4 6 1 4 6
4 5 7 4 5 8 2 5 7 2 5 8
6 8 9 6 7 9 3 8 9 3 7 9
1 2 4 1 3 4 1 2 7 1 3 7
3 5 6 2 5 6 3 5 8 2 5 8
7 8 9 7 8 9 4 6 9 4 6 9
There are... 42... of them. There is only 1 1x1 Young tableau, and there are 2 2x2 Young tableaux, of course; that there were 42 3x3 Young tableaux, and 24,024 4x4 Young tableaux was only recently established.
The square Young tableaux are only a subset of all the Young tableaux, but it is the square ones which are connected to the Riemann zeta function. A general Young tableau might look like this:
1 3 4 7 9 2 5 6 8
and these are associated with the theory of partitions and permutations and numerous other areas of mathematics as well.
Could Douglas Adams have come across this particular mathematical fact?
As we have seen on the previous pages,
infinity
---------- __________
\ \ | | 1
\ 1 | | ------------
zeta(z) = > ---- = | | 1
/ z | | ( 1 - ---- )
/ / i _| |_ x
---------- p in P p
i = 1
where z=x+iy for x and y real, and x > 1, and P is the set of prime numbers {2, 3, 5, 7, ...}.
Bernhard Riemann, in his original paper, extended the definition of what is know known as the Riemann zeta function to the entire complex plane by means of the following integral:
infinity
_
/ \ (z-1)
i | (-x)
zeta(z) = -------------------------- * | -----------, dx
2 * gamma(z) * sin(pi*z) | x
\_/ e - 1
- infinity
from which it was possible to derive the following symmetry property of the Riemann zeta function:
zeta(z)
------------------------------------------------
zeta(1-z) = z (z-1) pi * z
2 * pi * gamma( 1 - z ) * sin ( ------ )
2
This property can be used to define a function related to the Riemann zeta function which is symmetric around the critical line (that is, the line in the complex plane of values with real part equal to 1/2). In order to do that, it needs to be changed to this symmetric form:
-(z/2) z -((1-z)/2) 1-z
pi * gamma(-) * zeta(z) = pi * gamma(---) * zeta(1-z)
2 2
allowing the function
-(z/2) z
xi(z) = pi * gamma(-) * zeta(z)
2
to be defined, symmetric around the line z = (1/2) + (i * u). Of course, if we then define another function as xi((1/2) + (i * z)) we get one symmetric around the real axis, with the non-trivial zeroes on the real axis, which is even more convenient.
An astonishing fact about the Riemann zeta function is noted on the Wikipedia page about it:
infinity
________
\
1 \ mu(i)
------- = > -------
zeta(z) / z
/_______ i
i = 1
This is true for z=x+iy where x is greater than 1. If and only if the Riemann hypothesis is true, that hypothesis being that the Riemann zeta function is only equal to zero at the trivial values of -2, -4, -6, and so on, and at nontrivial zeroes, at values of the argument with a nonzero imaginary part, with real part equal to exactly 1/2, then the expression above is also true where x is greater than 1/2.
Since the analytic continuation of a function is unique, one would think at first glance that this amounts to a proof of the Riemann hypothesis.
However, mu(i) is the Möbius function of i. mu(1)=1; for other numbers, mu(i) is zero for any number that has the square of any prime number as a factor, it is 1 for any prime number and for the product of an odd number of distinct primes, and it is -1 for the product of an even number of distinct primes.
For x greater than 1, the sum over i equal to from 1 to infinity of 1/(i^z) converges, and is the Riemann zeta function of z. For x less than or equal to 1, this sum diverges.
Thus, it is entirely possible that the expression above for the reciprocal of the zeta function might fail when x is greater than 1/2, but less than or equal to 1, not by being equal to a different analytic function of z, but instead because the series fails to converge, depending on properties of the distribution of the prime numbers, which are exactly what the truth or falsity of the Riemann hypothesis can tell us about. A series can fail to converge without indicating an infinite value; for example, 1 + (-1) + 1 + (-1) + 1 + (-1) ... does not go to infinity, but keeps alternating between 1 and 0 as a sum, and therefore has no one number as a limit as the sum is continued to infinity.
Also of interest here is a definition for the Riemann zeta function that makes use of a series resembling the one for x > 1 but which extends into the range where that series diverges, which is given in Introduction to Analytic Number Theory by Apostol:
n
________
\ (1-z)
\ 1 n
zeta(z) = lim > ( ---- - -------- )
n -> infinity / z 1 - z
/_______ i
i = 1
which applies for x between 0 and 1, again, where z = x+iy.
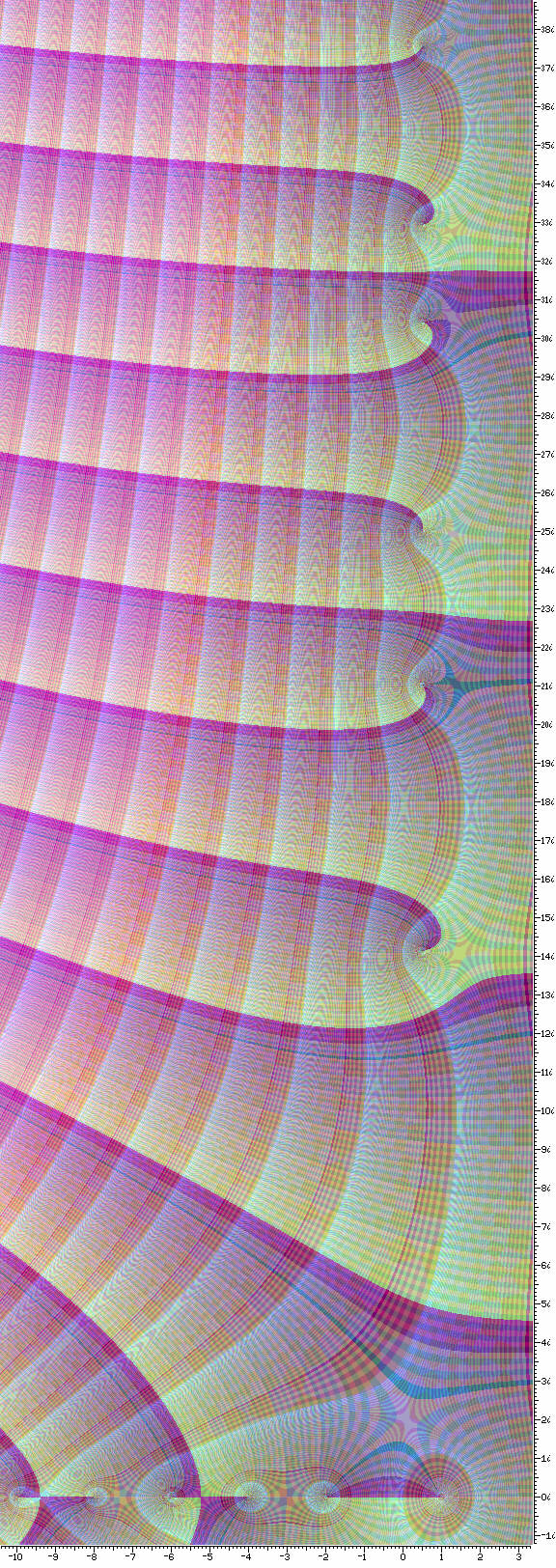
Now, here is an image of the Riemann zeta function, over a section of the complex plane including the real line near the bottom of the image:

On this diagram, with the aid of the scales provided, you can see the simple pole at 1, the trivial zeroes at -2, -4, -6, -8, and -10, and the first six non-trivial zeroes at
1/2 + 14.13472... i 1/2 + 21.02204... i 1/2 + 25.01085... i 1/2 + 30.42487... i 1/2 + 32.93506... i 1/2 + 37.58617... i
It was calculated using an efficient method developed by Jonathan Borwein, also known for his work on an efficient method for generating individual digits of pi.