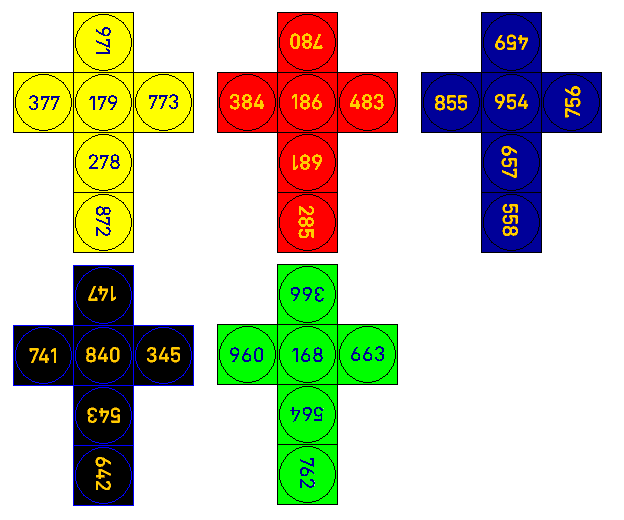

At right are depicted a set of dice with three-digit numbers on each face. I owned a set from childhood; they are used for a magic trick in which it is possible for someone who knows the secret of these dice to perform rapid addition.
Here is a diagram showing the complete layout of numbers on these dice.

In searching for another set of these dice, I learned some information about them. These dice are called "Phenomen", or, in English-speaking countries, "Phenomenon", and they were made in West Germany during the 1960s or thereabouts.
However, these dice weren't originated there.
David Balducci is credited as having originally come up with the idea for the magic trick, and then in 1927 the first set of dice embodying it was marketed as "The Di-Ciphering Trick" by Royal Vale Heath, who later wrote the book Mathemagic, and also much later introduced Martin Gardner to flexagons, the topic of his first Mathematical Games column.
Neither that original set of dice, nor ones for this trick that are currently available from a number of sources, some in wood and some in plastic, are as colorful as this set.
However, this set that I recently obtained, like the one that I originally had, has a problem with the gold ink or paint for the numbers on the green die for some reason.
The instructions that came with the dice explain how to work the trick:
Roll the dice. Add together the last digit of the number on each die. Subtract that total from 50; the result is the first two digits of the total of the complete numbers on all the dice, and the original total is the last two digits.
Looking at the numbers on the dice, it's not hard to figure out why the trick works:
Yellow 179 278 377 773 872 971 Red 186 285 384 483 681 780 Blue 459 558 657 756 855 954 Black 147 345 543 642 741 840 Green 168 366 564 663 762 960
Each one of the five dice has the following two properties: the middle digit of each number is the same, and the first and last digits of each number always sum to the same total.
Middle Digit Sum of First and Last Digits
Yellow 7 10
Red 8 7
Blue 5 13
Black 4 8
Green 6 9
So the sum of the first digits is equal to 47 minus the sum of the last digits. And the middle digits add up to 30, contributing 300 to the sum of the numbers on the dice; and so 47 plus 3 makes 50.
It is possible to improve these dice, though.
The numbers on the blue die could be replaced by the following and the trick would still work:
162 261 360 459 657 954
even though now the middle digit isn't always the same!
How does this work?
Well, we're using the fact that the first and last digits always add to 13 on the blue die. By allowing the first digit to be 1, 2, or 3, the last digit would therefore be 12, 11, or 10. Of course, though, those aren't single digit numbers.
So the last digit becomes 2, 1, or 0, and the leading 1 carries over to increase the middle digit. This makes the pattern behind the design of the dice less obvious.