The SOMA cube puzzle is just one of several famous inventions of Piet Hein.
He is known as the author of a book of poetry, entitled Grooks; one of his first well-known inventions was the game of Hex, and he is also known for proposing the "superellipse" as a curve that is intermediate between the ellipse and the rectangle.
In his book Winning Ways for your Mathematical Plays, mathematics professor John Horton Conway examined a number of games and puzzles in a more serious manner from a mathematical viewpoint than had heretofore been attempted, particularly in a treatise still aimed at a relatively general audience.
It began by noting that in a 3 by 3 by 3 cube, eight of the cubes corresponded to the corners, or vertices, of the cube, twelve of them to the edges of the cube, six of them to the faces of the cube, and one to the center of the cube.
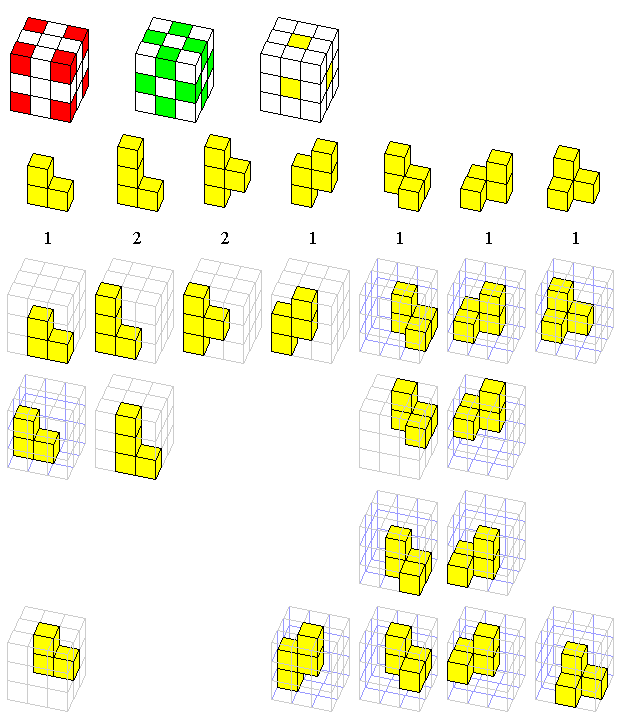
Along the top of the diagram, the vertex cubes are shown in red, then the edge cubes are shown in green, and finally the face cubes are shown in yellow.
Given the shapes of the various SOMA pieces, only so many of the cubes in them could be placed in a corner of the cube. In fact, for the entire set of pieces, only nine of them could fit in a corner. So, that meant that of those nine possibilities, for any solution of the cube, it was necessary that all but one of the possibilities would need to be used.
The third SOMA piece shown in the diagram above could be placed so as to fill two of the cube's corners. But it could not be placed so as to fill just one, and since two possible corner cubes could not be spared, this meant that the piece could only be placed in the cube in one basic way (although, of course, it could still be placed according to any of the 24 possible ways the cube could be oriented).
Similar arguments also involving the face and edge pieces allowed him to narrow down the possible ways in which any of the other pieces could be placed in the cube to at most four for each piece. Particularly surprising is that in the SOMA puzzle, the first piece, the one composed of only three cubes, cannot be placed with its corner in one corner of the cube - which, at least for most cube puzzles including such a piece, would tend to be the left-over position in which one would most expect it to end up.
The diagram shows, below each piece, the possible positions for it in each of the four categories of orientation which Conway identified.
The first row shows the Normal position of each piece, in which it does not occupy the one central cube, and in which it occupies the maximum number of vertex cubes that it can.
The second row shows the Deficient position of each piece, in which it also does not occupy the one central cube, and in which it occupies one less than the maximum number of vertex cubes that it can.
The third row shows the Central position, where the piece occupies both the maximum number of vertex cubes that it can, and the central cube.
And the fourth row shows the Central and Deficient position.
As noted above, one and exactly one piece may be in a Deficient orientation. And since there is only one cube in the center, one and exactly one piece may be in a Central orientation. The same piece could be in an orientation having both of those qualities, in which case it would be in the Deficient and Central orientation shown in the bottom row.
This book featured the Somap. This was a chart showing 240 of the 480 possible solutions of the SOMA cube puzzle, and how 239 of those solutions were related in that one could change a cube from one solution to a related one by removing only two, or sometimes three, pieces, and, by changing those pieces around, produce a combination of those pieces with exactly the same shape to replace in the cube.
Since only two of the SOMA cube pieces are not laterally symmetric, and the two that are not are mirror images of each other, for every solution of the SOMA cube, its mirror reflection can also be formed. It is because only one version of each solution is included in the Somap that only 240 of the solutions, not 480, are present there.
This diagram illustrates the special solution of the SOMA cube that isn't connected in this way to other solutions:
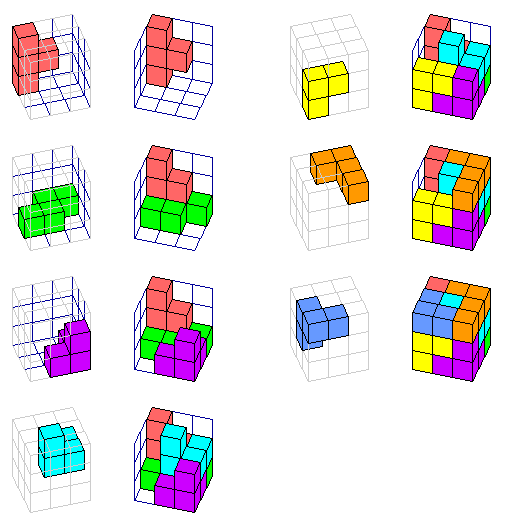
Each piece is shown in its position in the cube from one viewpoint, and the cube, with the pieces added one at a time, is shown from a slightly different viewpoint, which should help make it very clear where each piece is in the finished cube.