This is a rather open-ended topic which is at least an excuse for a few pretty pictures.
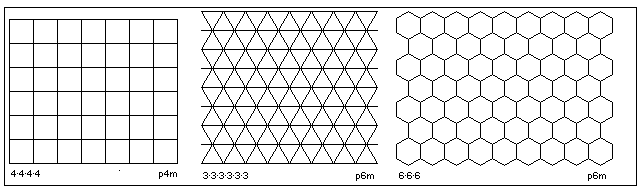
After all, there are a lot of utterly trivial ways to fill space with polyhedra. To start with, since we can tile the plane in the following fashions with regular polygons,

then we can tile space with prisms with those polygons as bases.
And, indeed, we can stretch the tiling with squares, so that any rectangle will do. In fact, it can even be sheares; parallelograms will do!
The tiling with equilateral triangles can be stretched, as well!
So any isosceles triangle will do!
We can split the rectangles in half, so any right triangle will do; wait a moment, we can split the parallelograms in half, and so any triangle whatever will do as the base for a space-filling prism!
Well, given that we can easily fill space with cubes, let us look at an obvious consequence of that.
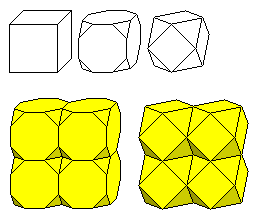
If we stack up truncated cubes in the same way as we would stack cubes, then between the corners, there are empty spaces that can be filled with octahedra. And the same is also true if we stack up cuboctahedra instead, except this time, the octahedra will be bigger, and will touch at their corners.
If we go still further in the same direction, we will come to the truncated octahedron. As can be seen in the diagram below,
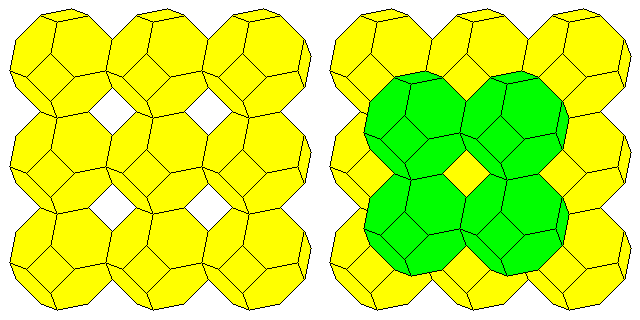
this shape will fill space all by itself; it goes just slightly beyond needing octahedra to fill the voids it leaves, with just the right overlap so that it is the truncated octahedron itself that fills those voids.
The truncated octahedron fills space in the Body-Centered Cubic arrangement.
If, instead of starting with a large and complex shape like the truncated cube or the cuboctahedron, we start with the octahedron itself, then, as the diagram below shows:
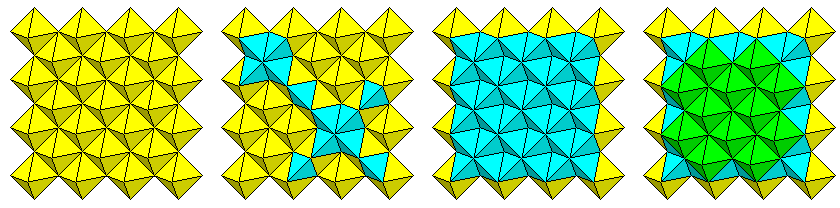
if we place octahedra side by side, at their edges, to form a square array, the spaces between them are just perfect for being filled with tetrahedra. And after a layer of tetrahedra is placed, the assemblage is ready for another layer of octahedra.
On my page about Sphere Packing, I had another image illustrating how space is filled with octahedra and tetrahedra working together,
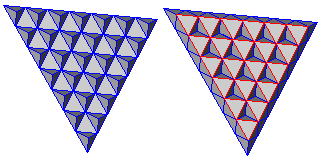
but this time, I started by putting the tetrahedra in a triangular array, then filling the gaps between them with octahedra.
On both the page about Sphere Packing and the page on Hexagonal Three-Dimensional Chess, I discuss the Face-Centered Cubic arrangement.
The rhombic dodecahedron is the one Archimedian dual (the dual of the cuboctahedron) which can fill space, and they fill space in that arrangement.
The illustration below:
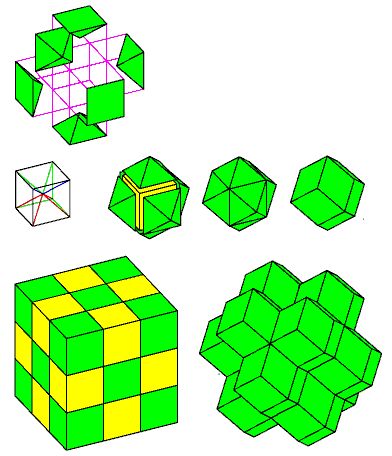
shows how this works.
Start with space being filled with cubes that alternate between green and yellow in color, as shown in the lower left of the image.
The drawing in the center left shows how a cube can be divided into six pyramids, and the portion of the image in the upper left shows one of the green cubes being exploded into its six component pyramids.
In the center of the diagram, after the outline drawing, we see one of the yellow cubes having one pyramid from each of the six adjacent green cubes being added to it; first, they approach it, then they touch it, and then the lines between pairs of pyramids, where they match in slope, so that two triangular faces from two pyramids form a single rhombic face of the rhombic dodecahedron, are removed.
On the bottom right of the diagram, we show the part of the space-filling arrangement incorporating the rhombic dodecahedra made from the yellow cubes in the cube on the bottom left.
Since both the Body-Centered Cubic and Face-Centered Cubic symmetries have been mentioned above, here is the most common type of diagram used to illustrate these two arrangements:
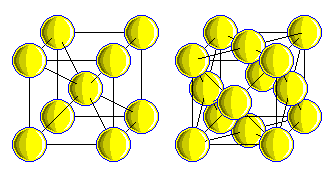
with the Body-Centered Cubic shown on the left, and the Face-Centered Cubic shown on the right.
Back to the Archimedian solids and the Platonic solids: other interesting combinations of different solids exist. For example, as this diagram shows,
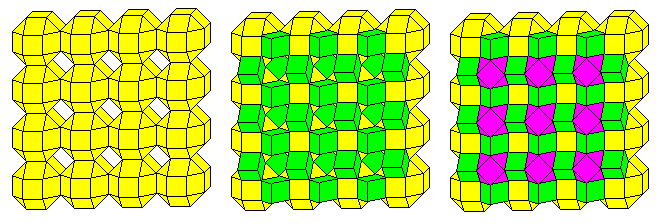
one can start with a square array of small rhombicuboctahedra (yellow). The second diagram, in the center of the image, shows how cubes (green) can be added to the obvious cube-shaped gaps; and the third diagram, on the right, shows that the next natural step is to add cuboctahedra (purple), which now leave gaps for another layer of small rhombicuboctahedra to begin the cycle again.