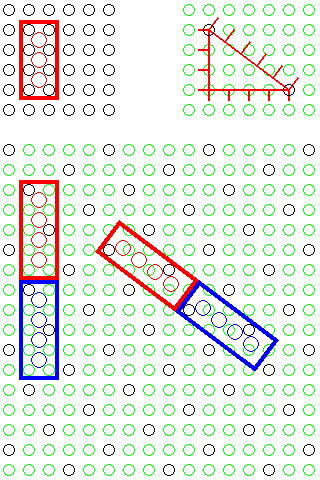
We all remember those high-quality building blocks made by a Danish company we played with as children. Recently, when they came out with building sets to make castles, it occurred to me that it would be nice if it were possible to build walls at odd angles. Although a 45 degree angle would be ideal, that would require a whole new assortment of block types which could only be used at a 45 degree angle. Thus, it occurred to me that one could build walls at an odd angle using existing blocks if one made use of the Pythagorean theorem, and the simplest 3-4-5 Pythagorean triplet, by using a building surface on which only one out of every five studs that would normally appear are present:

In the bottom part of the diagram, the black circles indicate the studs that are actually present. Mats with the pattern shown, but in its mirror-reversed form, and mats where the changeover occurs along a normal 45 degree diagonal, plus extra blocks which allow a continuous wall to change direction, would also be needed.
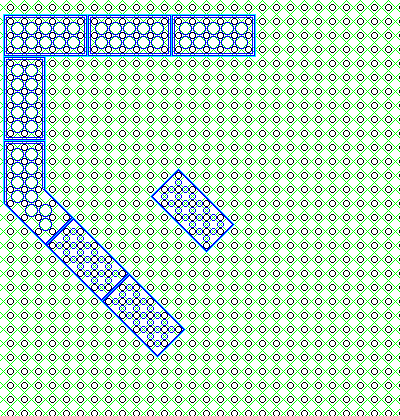
Thus, this diagram shows the blocks required to change direction between bricks running in one angled direction and in orthogonal directions, in two sizes to permit walls to interlock firmly:
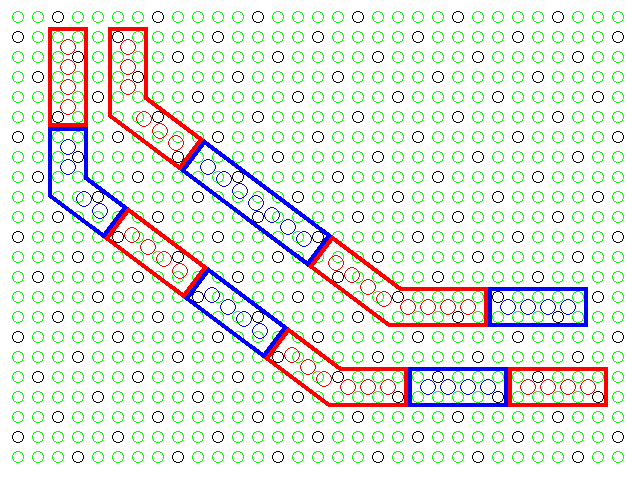
and, when a building base reverses parity along a diagonal, in the diagram shown from the lower left to the upper right, this shows the piece, in two sizes, required for a change of direction between blocks running in angled directions in the two different regions of the base.
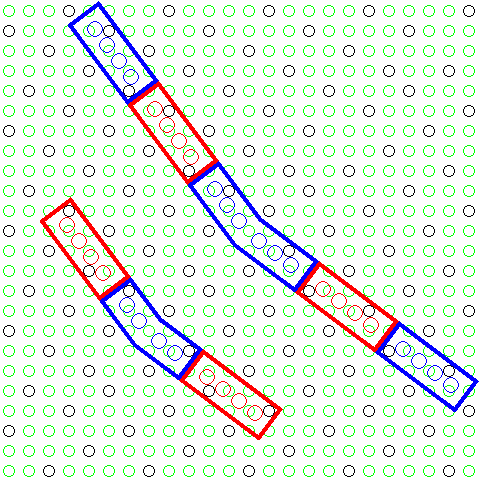
But one thing that the above diagrams do not make clear, with their carefully chosen locations for the blocks which are used at the points the walls change angles, is how limited the choice of positions for these blocks actually is. The diagram below,
showing the effective grids on which blocks running at the different angles are placed shows that, in the first of the two previous diagrams, the block at the upper left, bent at the sharpest angle, belongs to one of two different families. Blocks belonging to both families would be required if an angled roof were to be placed atop a castle or other structure with a wall with such a bend. The block with the shallower angle at the lower right of the top diagram belongs to one of three families.
And on the right of the diagram here, the case for the block at a very shallow angle, in the second of the two previous diagrams, which illustrates a mat where the parity of the pattern of studs left present reverses along the diagonal, is illustrated. That block belongs to one of seven different possible families.
This level of complication may be felt as a major shortcoming, and limitation of flexibility, in the kind of block I propose, and may well be the reason why it was rejected if the idea occurred to others.
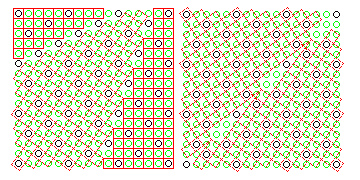
Also, while usually there would be a change from slanted blocks to straight blocks as depicted above, sometimes it might be desired to change directly from slanted blocks going in one direction to slanted blocks going in the other direction where the parity reverses along an orthogonal line. The diagram below illustrates that one would need four types of block for the shallower bend that would occur in such a case, and three types of block for the sharper one:
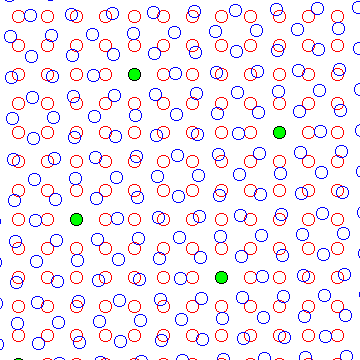
In practice, however, since such reversals of parity would occur at the junction of two independent mats, if blocks at these angles were provided, they would not belong to the families of types which those diagrams imply, but instead to the ones visible in the diagram below:
where the axis of symmetry is halfway between two adjacent studs rather than down the middle of a stud.
Of course, the 3-4-5 Pythagorean triangle, while it provides the opportunity to place walls at an angle, does not allow placing them at the most popular angle, that of 45 degrees. A closer approximation to that angle might be obtained using the 20-21-29 Pythagorean triangle; grids of equal spacing, tilted relative to each other by the angle of the hypotenuse of that triangle would not coincide as often as those determined by the 3-4-5 triangle, but they would still do so reasonably often, as illustrated by the diagram below:
However, a system designed with smaller studs would have no problem including special blocks designed to be set at a 45 degree angle:
Another way to allow bricks to be placed at more angles would involve treating the vertical and horizontal directions sepaarately, so that the fundamental symmetry would be of another type, allowing twelve-sided constructions:
This does have the disadvantage that a 45 degree angle is, basically, not possible; but it does make it obvious how to use the alternate angles that are provided.
Looking at a photograph of the Great Wall of China, I was inspired to think of how a set to construct a replica of it at a larger scale could be made if one were to make curved bricks, in a graded set of curvatures suitable for making concentric rings of bricks.
Further thought led me to decide that the angle that would be the fundamental unit for such bricks would have to be based on the Pythagorean triangle. It happens that the 3-4-5 Pythagorean triangle would provide an acceptable scaling for stairs, in terms of rise over run, but then there's the additional complication that the vertical scaling of the kind of bricks in question is not the same as the scaling in the two horizontal directions.
The fundamental distance horizontally from one stud to the next is 8 mm, and the fundamental distance vertically is one-third the height of a brick, which is 3.2 mm.
But for the hypotenuse to relate to the horizontal scale, allowing bricks to be built at a tilted angle, an actual Pythagorean triangle, not a squashed one, is needed. Fortunately, however, the two distance scales are related.
The vertical unit, 3.2 mm, times five is 16 mm, and the horizontal unit, 8 mm, times two is also 16 mm.
While the 3-4-5 triangle would give a suitable angle for stairs, preferably a smaller tilt ought to be the basic angle. This could always be repeated, and that way there would be a choice of angles.
The 7-24-25 triangle gives an angle of tilt of about 16.26 degrees. The 3-4-5 triangle gives one of about 36.87 degrees. So this would be usable, although a smaller angle of tilt, allowing more choices, would be desirable.
Another possible choice is the 15-112-113 triangle. Here, the angle of tilt is about 7.63 degrees, and not only is the horizontal distance of 112 a multiple of two, but the vertical distance of 15 is a multiple of three. A normal stairway tilt is divided into four parts by this triangle, instead of two.
The horizontal distance has to be a whole number of studs, 112 studs, for the hypotenuse to be one stud longer, at 113 studs. So the horizontal distance is 112 times 8 mm, which means the vertical distance is 15 times 8 mm, or 120 mm.
Given a basic vertical unit of 3.2 mm, five such units are 16 mm, five brick heights are 48 mm, and twenty-five brick heights are 240 mm. So, in order to fit, a wedge of this type would have to be 224 studs long.
Ignoring this consideration, and allowing the height to be 12 1/2 blocks, the diagram below:
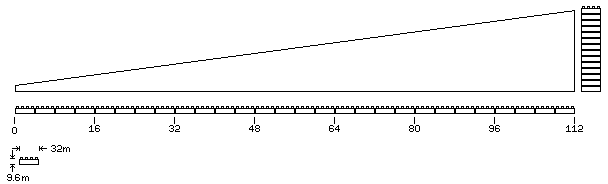
shows what a block of this nature would look like. Since the incline is shallow, one extra block height would be included below the wedge part so that studs could fit.
Clearly, however, that is too large to permit flexibility in building structures.
On the other hand, the 7-24-25 triangle is significantly smaller. Since whole studs are required along the hypotenuse, it doesn't seem like the fact that the base is divisible by three can be exploited.
The minimum height would be 7 vertical units of 3.2 mm, or 22.4 mm. That would make the base 24 vertical units, or 76.8 mm. Multiplying that by five, one would get 384 mm, which is 48 studs, so this smaller triangle also needs to be multiplied by two to get both a whole number of studs and a whole number of vertical units.
That would lead to something like this,
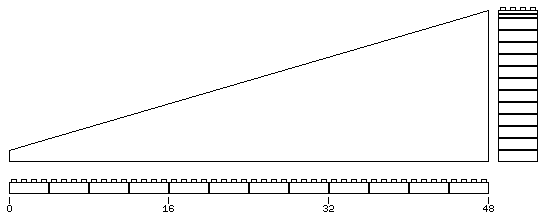
which is still fairly large, but not totally unreasonable.