A long time ago, it was thought that physics falsified Darwin's theory of evolution, because while the gravitational collapse of the Sun could produce enough energy for it to shine, it would only be able to do so for a few million years, which fell short of the eons required for evolution.
But now we know that the Sun is a fusion reactor.
In our own efforts to harness thermonuclear power, we attempt to construct two kinds of fusion reactor: magnetic confinement reactors, in which a suitable magnetic field keeps ionized deuterium and tritium gas at a very high temperature together at an adequate pressure for fusion to take place, and inertial confinement reactors, in which a pellet of frozen deuterium, tritium, and/or lithium-6 is hit with beams from several powerful lasers, and cannot explode fast enough to avoid producing energy through fusion.
Inertial confinement, of course, can work, as it is the principle behind the hydrogen bomb, but it has not yet been made to work on the small scale suitable to power generation.
Magnetic confinement is difficult, because the way magnetic fields interact with electrical charges is to restrict motion in some directions and not others, leading to the need to use a shape such as a torus, instead of a sphere, to confine the fuel and the reaction - and to difficult problems with instabilities.
Electrostatic confinement could keep positively charged ionized deuterium and tritium confined in a spherical volume in a straightforward manner, but to do so to the extent required for fusion would require wholly impractical voltages. Stars, however, achieve the same thing in a natural fashion, thanks to their large scale, by means of gravitational confinement.
The age and the mass of a star determine the kinds of nuclear reactions that take place within it.
The smallest stars, known as brown dwarfs, produce energy through the fusion of deuterium (heavy hydrogen) nuclei, and the largest brown dwarfs also burn lithium; these stars, however, are not large enough to produce a high enough internal temperature to fuse ordinary hydrogen, without a neutron in the nucleus, and thus they never become part of the Main Sequence.
Stars on the Main Sequence, a region on a chart showing a star's spectral class (a form of notation for its color temperature) versus its absolute luminosity, called the Hertzsprung-Russell diagram, in which the largest density of stars is usually found, derive their energy primarily from the fusion of ordinary hydrogen.
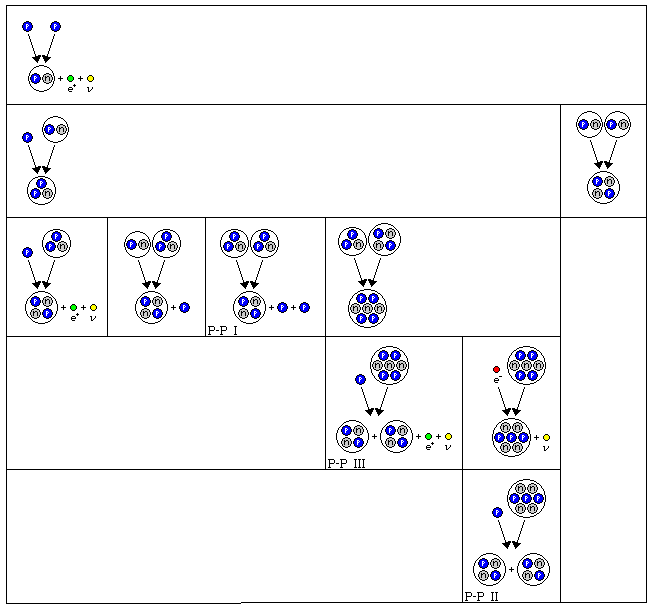
There are two important ways in which ordinary hydrogen (protons) is turned into helium-4 (alpha particles) in stars.
One is for this to happen directly; two protons collide, throwing off a positron and an electron neutrino to become a deuterium nucleus, and then another proton collides with that to produce a helium-3 nucleus. Two helium-3 nuclei can then collide to produce two protons and one helium-4 nucleus.
Other paths are possible; for example, two deuterium nuclei could collide, or a proton could hit a helium-3 nucleus, leading to a helium-4 nucleus, a positron, and an electron neutrino.

The image above illustrates some of the possibilities. It is divided into six columns from left to right, each column depicting a series of events that lead to the production of helium-4 nuclei from protons.
The rows indicate the steps in the processes. The first step is always two protons combining to produce a deuterium nucleus, with the emission of a positron and an electron neutrino.
Having protons and deuterium nuclei around, there are two possibilities at the second level. A proton could hit one of the deuterium nuclei to produce helium-3. Or two deuterium nuclei could collide and produce a helium-4 nucleus immediately. But this latter event hardly ever happens, because in the conditions within most stars, deuterium nuclei combine with protons almost immediately. Deuterium fusion, however, as noted above, is an important process in brown dwarfs.
Then, on the third level, one possible third step might be a proton hitting a helium-3 nucleus to form helium-4, with the emission of a positron and an electron neutrino. This also very seldom happens, despite protons being common. Presumably, this is because there are no resonances which increase the cross-section of this reaction. The third step possibility in the second column involves the helium-3 nucleus being hit by a deuteron, and we've seen above that there are not many deuterons around.
Having disposed of columns 1, 2, and 6, we are left with the three possible forms of the proton-proton chain that actually are important in main sequence stars.
The proton-proton I chain involves two helium-3 nuclei combining, to form a helium-4 nucleus and two extra protons.
The other two possibilities involve a third step in which a helium-3 nucleus hits a helium-4 nucleus, which acts as a catalyst in the process. In this step, beryllium-7 is formed.
In the fourth step, the difference between columns 4 and 5 becomes visible. In column 4, the beryllium-7 nucleus is hit by a proton; the result ultimately decays into two helium-4 nuclei and a positron and an electron neutrino are emitted. This is the proton-proton III chain.
As the Sun and other stars are electrically neutral, they aren't composed only of protons and other positively-charged nuclei. Electrons are also present, and one of those can hit the beryllium-7 nucleus. When this happens, a proton changes to a neutron, giving us a lithium-7 nucleus. Since both a proton and a neutron have spin 1/2... and so does an electron... an electron neutrino is emitted to conserve spin, just as happens when a positron is emitted because a proton spontaneously changes to a neutron in a proton-heavy nucleus.
Column 5 continues with the fifth step in the proton-proton II chain, where the lithium-7 nucleus is hit by a proton, yielding two alpha particles.
The other major alternative is known as the carbon cycle, or, more recently, as the CNO process. Here, a carbon-12 nucleus is successively hit by four protons, changing its nature, and leading to positrons and neutrinos being emitted at times as protons change to neutrons, this happening twice during the cycle, until finally a helium nucleus is thrown off, and we have a carbon-12 nucleus again to start the cycle over.
The helium nucleus is thrown off when the nitrogen-15 nucleus the cycle produces is hit by another proton, thus avoiding the objection that oxygen-16 is a stable isotope. (Oxygen, in the form oxygen-15, does occur earlier in the cycle.)
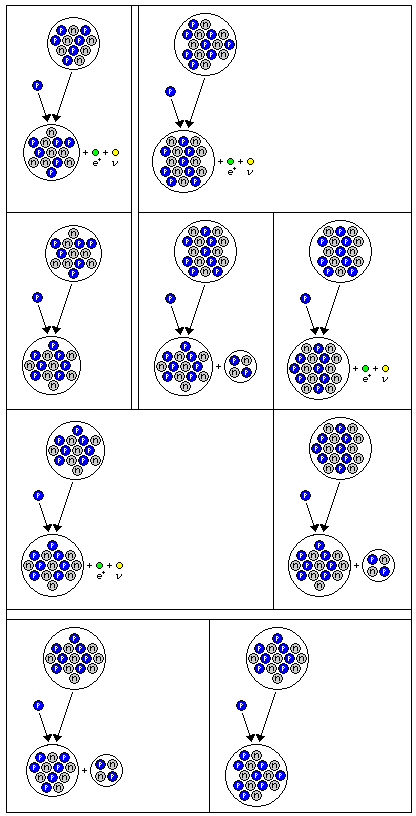
The diagram on the right shows the CNO cycle, or the CNOF cycle, in detail, including the alternate paths it may take.
The main cycle is shown in the first column. In the first step, a proton hits a carbon-12 nucleus, producing carbon-13 and a positron and an electron neutrino.
Then, another proton hits the carbon-13 nucleus, creating nitrogen-14, as the second step.
In the third step, a proton hits the nitrogen-14 nucleus, creating nitrogen-15 and a positron and an electron neutrino.
When another proton hits the nitrogen-15 nucleus, two things can happen. A carbon-12 nucleus and a helium nucleus can be produced; this starts the main cycle over from the beginning. The other possibility is that oxygen-16 will result. In that case, the alternate form of the cycle begins, which will continue in the top row of the diagram in the second column.
When the oxygen-16 nucleus is hit by a proton, the result is an oxygen-17 nucleus, a positron, and an electron neutrino.
When an oxygen-17 nucleus is hit by a proton, two things can happen.
In the first case, we return to the main carbon cycle when nitrogen-14 and helium-4 nuclei are produced.
In the second case, we continue down a side branch of the alternate sequence, shown in the third column of the diagram. The oxygen-17 nucleus becomes an oxygen-18 nucleus, throwing off a positron and an electron neutrino.
In that case, when the oxygen-18 nucleus is hit by another proton, the result is nitrogen-15 plus helium 4, and so we return to the two possibilities when nitrogen-15 is hit by a proton that are common to both cases of the cycle.
Note, incidentally, that when a nucleus emits a positron and an electron neutrino as the result of being hit by a proton, this does not happen immediately, but is instead the result of radioactive decay of the nucleus with a proton added before a proton changes to a neutron. Thus, the diagram doesn't show, for example, the fluorine-16 nucleus which decays to the oxygen-16 nucleus shown there, to which the alternate name of CNOF cycle is owed.
At one time, it was thought that our Sun was powered by the carbon cycle. We now know that while this process does take place in the Sun to a limited extent, most of the Sun's energy is produced by direct hydrogen fusion. In larger stars, with hotter internal temperatures, the carbon cycle plays a larger role; the cross-over point is at a mass of one and one-half times the mass of the Sun.
Stars with masses from about half that of the Sun to masses ten times that of the Sun become red giant stars as they near the end of the hydrogen-burning portion of their lives. In such a star, hydrogen fusion takes place in the outer part of the star, while the helium produced accumulates in the core of the star.
Half the mass of the Sun is also the lower limit of the stellar mass required to eventually begin fusing helium nuclei to form carbon-12 nuclei, in the triple-alpha process. A value of two and one-quarter times the mass of the Sun is also significant; stars below this limit enter a phase where the helium core is kept from gravitational collapse more by quantum mechanical effects than by thermal pressure; the result of this is that in these smaller stars, the start of helium burning is more violent, marked by a phenomenon called the helium flash, because degenerate matter is a very good thermal conductor.
Carbon can combine with an alpha particle to produce oxygen, and oxygen can combine with an alpha particle to produce neon. In stars that are larger than about eight times the mass of the Sun, this can continue with neon combining with an alpha particle to produce magnesium, or with two carbon nuclei or two oxygen nuclei combining.
Stars in which this takes place usually go on to become Type II supernovae. An alpha particle hitting a neon nucleus produces energy, and this can continue up to silicon and beyond and still produce energy, but this comes to an end with iron.
When a star runs out of energy, gravity takes over, and the star shrinks. In the case of these large stars, the collapse is a violent implosion, and because what is left of the star is larger than 1.4 times the mass of the Sun (the Chandrasekhar limit), without heat energy to expand the star, it cannot resist gravity through electron degeneracy. This means that instead of remaining a white dwarf, gravity continues to crush it until it becomes a neutron star, held apart by the degeneracy pressure of the neutrons instead. At still higher masses, about ten times that of the Sun, the central part of the star can become a black hole, and the rest of the star is involved in a violent explosion.
Several types of stars have unusual characteristics of particular interest.
Cepheid variables are very important in astronomy because of the period-luminosity relationship discovered by Henrietta Swan Leavitt. This lets us determine the distances of distant galaxies where parallax is not available as a tool.
This is now believed to be caused by a phenomenon known as the Eddington valve: an outer layer of helium absorbs some of the outgoing light from the star, but as this layer is warmed and expanded from doing so, it no longer blocks as much of that radiation, and so cools off, and returns back to its former state, thus repeating the cycle.
Incidentally, conventional eclipsing binaries, where a star is variable because it is really two stars orbiting each other, are not useless to astronomers, even though their orbital characteristics are arbitrary. Of course, the period of any variable star we can observe can be known; but even when we can't see the two stars separately, Doppler shifts in their spectra let us determine the speed at which they move which is equivalent to knowing the radius of the orbit; and so eclipsing binaries let us determine the masses, not only of the individual stars of which they are composed, but of stars in general of those types.
T Tauri stars are young stars that have not yet started the portion of their lifespan spent on the Main Sequence. The energy that makes them shine is thought to derive partly from contraction due to gravity, and partly from fusion reactions which consume lithium, which take place at lower temperatures than normal hydrogen fusion. (A different designation, "Herbig Ae/Be stars", is applied to young stars with masses twice that of the Sun or greater.)
Wolf-Rayet stars, on the other hand, are a type of older star that has left the Main Sequence. These stars were originally very massive, twenty or more times as massive as the Sun. They are distinguished by ejecting large quantities of matter as they shine. Some of them have begun to produce their energy through burning helium to produce carbon. They may end their lives as supernovae, but not as Type II supernovae.