Until 1972, there were 24 hours in a day, 60 minutes in an hour, and 60 seconds in a minute, and that was that.
Almost. Because, although that was indeed how time was labelled, the second as used to define units of measurement in terms of each other was shorter, by a slight amount, than the second used to tell time. A scale of time based uniformly on the second of measurement had been in use by astronomers since 1952 (although it became officially recognized either in 1958 or 1960, depending on which web page you go by), called Ephemeris Time. Before 1972, Ephemeris Time was replaced, first by Terrestrial Dynamic Time and then by Atomic Time: TAI first was kept in 1958.
What happened in 1972 was that we changed to using the second of uniform length that had already been defined, and kept the time on our clocks in close harmony with mean solar time by adding an extra second at occasional intervals.
From 1959 to 1972, apparently the changes in the time scale were as shown below, but the information I have found on the Internet so far has some gaps:
Year Frequency Time steps
Offset
-10
(* 10 )
1958 -100
1959 -170 (or -100?)
1960 -150
prior to 1961, 29 time steps, each of
20ms, took place
1961 -150 August 1, +50ms
1962 -130
1963 -130 November 1, -100ms
1964 -150 April 1, -100ms
September 1, -100ms
1965 -150 January 1, -100ms
March 1, -100ms
July 1, -100ms
September 1, -100ms
1966 -300
1967 -300
1968 -300 February 1, +100ms
1969 -300
1970 -300
1971 -300
1972 January 1, 107.758 ms
(to inaugurate the present UTC)
where a step of -100ms means an interpolated "leap" 100 milliseconds, and a step of +50ms or +100ms means a skipped 50 or 100 milliseconds. (That the 50ms step was one of 50 skipped milliseconds is something I could confirm from a table of TAI-UTC going back to 1961 that appears in several places on the Web, its original source being the U.S. Naval Obervatory.)
After 1972, multiple sources give the dates on which leap seconds have occurred so far:
1972 June 30, December 31 1973 December 31 1974 December 31 1975 December 31 1976 December 31 1977 December 31 1978 December 31 1979 December 31 1981 June 30 1982 June 30 1983 June 30 1985 June 30 1987 December 31 1989 December 31 1990 December 31 1992 June 30 1993 June 30 1994 June 30 1995 December 31 1997 June 30 1998 December 31 2005 December 31 2008 December 31 2012 June 30 2015 June 30 2016 December 31
There have not been any additional leap seconds since the one at the end of 2016 up to 2019. Thus, TAI - UTC remains at 37 seconds. Before the leap second on June 30, 1972, the original value of TAI - UTC was 10 seconds.
Although TAI is a constant, unchanging, sequence of SI seconds, like Ephemeris Time, it is not synchronized with it. Instead, TT - TAI is 32.184 seconds, where TT is Terrestrial Time, a modernized successor to Ephemeris Time which is intended to match it as closely as possible while being more accurate and precise.
So TT - UTC is currently 69.184 seconds.
The most convenient source of high-accuracy time easily available is perhaps devices using GPS, the Global Positioning System. It uses its own time system; that also is based on the standard SI second, and was in step with UTC when it was inaugurated on January 6, 1980.
As there have been 18 leap seconds since then, GPS - UTC, as of this writing (2019) is 18 seconds. So TT - GPS is fixed, like TT - TAI; TT - GPS is 51.184 seconds. Thus, if you meet Dr. Tony Newman and Dr. Douglas Phillips, you will be able to tell them the time to the nearest millisecond in terms that could be understood back in 1968, so they can finally be brought home!
The length of the SI second was based on work by Simon Newcomb which obtained the average length of the second between 1750 and 1892, so even on January 1st, 1900, the second of mean solar time was already longer than this. However, before the second was defined in terms of atomic vibrations, its formal definition was based on something else from noon, December 31st 1899: the length of the tropical year, which was to be divided into 31,556,925.9747 seconds.
Recently, objections have been raised to the inconvenience of adding in leap seconds, particularly because of the potential for difficulties if certain major Internet servers do not all make the correct adjustments for leap seconds. So the proposal has been made that we simply abandon the leap second. When the error in the time scale exceeds half an hour, we could always set our clocks back an hour, if we were so provincial as to insist on a fixed relation between the clock and the Sun, as we do each year when Daylight Savings Time (or Summer Time, as it is called in the UK) ends.
Such a proposal has, of course, been seen by many as unreasonable. If we restrict ourselves to the narrowest practical considerations, we might note that as the clock shifts with respect to the Sun, the energy-saving consequences of Daylight Savings Time would be disturbed.
UPDATE: On November 22, 2022, a vote at the International Bureau of Weights and Measures (BIPM: Bureau International des Poids et Mesures) has decided in favor of abandoning the leap second for a period of 100 years, starting in the year 2035, subject to the cooperation of the ITU. The advanced date for commencing this change in policy is due to techincal issues with the Russian GLONASS satellite positioning system.
The alternative to this that I am proposing here is based on the assumption that the following two premises are being held:
I am attempting to satisfy both conditions without losing the relationship between the time scale and the ordinary time of day.
One way to deal with this might be to permit a greater discrepancy between the civil time scale and mean solar time, and simply have a leap minute when appropriate. This would be perhaps once in a decade. This would reduce the inconvenience of making frequent adjustments, but the possibility that noticeable problems would result, as well as their severity, if the adjustment is not made somewhere is increased. Thus, while this might seem, at first, to be a better answer than what I am about to propose, because it is simpler, it actually fails to meet the first of the two requirements noted above.
Another way would be to approximate the situation that existed before 1972, but with modifications that would mean that the relationship between civil time on the one hand, and atomic time on the other, would remain mathematically exact instead of becoming vague.
There are 86,400 seconds in a day. In a year, there may be 365 or 366 days. If you add one second to a year, then, you could also instead lengthen the second by one part in 365 * 86,400 (and, in leap years, return to the ordinary second for December 31st). If two leap seconds are needed, the second could be lengthened twice as much, and so on.
The amount that would have to be added to the second to equal one leap second in a year would be about 31.7098 nanoseconds.
This might not, however, be a round number that is convenient to add to the second. It might be easier, for example, to add 32 or 31.75 nanoseconds to the second for part of the year. Or, if we view sexagesimal rather than decimal parts of the second as the fundamental unit, we could lengthen the second by one part in 360 * 86,400, and return to the ordinary second for the last five days of the year (six in leap years).
Or, we could go by the fact that the second is defined as 9,192,631,770 times the period of a certain oscillation of the cesium atom. That number is 2 * 9 * 5 * 49 * 47 * 44,351; as it happens, 294, which is 2 * 3 * 49, is a number of oscillations that is not too far over the amount we need to add to the second.
I have since discovered that the notion of adding a certain number of cesium oscillations to a second is based on a false premise: clocks using a cesium oscillator to provide their accuracy do not work by counting cesium oscillations, but instead count the oscillations of a quartz crystal operating at a much lower frequency, the frequency of which is calibrated by tuning it with respect to the frequency of the cesium oscillator. Incidentally, such a quartz oscillator would not operate at 32.768 kHz, as those in ordinary watches do, but instead it would likely operate somewhere in the 5 MHz - 10 MHz range, where it is possible to produce the highest quality quartz oscillators.
Thus, if we decide in a year needing one leap second to change the civil second to 9,192,632,064 such oscillations, we would revert to the normal second at 15 seconds after 9:24 PM (or 21:24:15) in this scale of civil time as nominal for the Prime Meridian on December 28th (December 27th in leap years), and we would have lost a second as required.
So instead of a second that varies continuously in length as the Earth's rotation gradually slows in general, and also is disturbed by both slowing down and speeding up in the short term, the length of the second would change only among the members of a specific family of lengths, and there would always be a definite mathematical relationship between the civil second and the absolutely uniform atomic second.
Since it is largely true that quartz oscillators, which keep to an accuracy of one second per year only with great difficulty, are the most accurate type of clock used in all but the most exotic application, and as this deals only with the second of civil time, not the second used for the constants of measurements, rubidium and cesium oscillators used by TV stations for calibrating their broadcast frequencies would not be involved, it would seem that there is no problem; only the atomic clocks used for the national standards would have to be given the ability to produce civil time in addition to atomic time.
I have been informed, though, that there are clocks used for Internet server applications that do use a rubidium oscillator to calibrate a high-quality quartz crystal at intervals (thus achieving the accuracy of rubidium without its power consumption); these clocks, though, usually keep themselves in step with GPS time. As it happens, the Global Positioning System uses a time standard that is simply atomic time with an offset; the time information from GPS includes no leap second information. Thus, something extraneous to such a system is needed to insert leap seconds at present, and so the adjustment to a civil time scale with a second of variable length would also admit of being done in software somewhere without making an expensive rubidium clock obsolete.
Other types of clock have different natural frequencies than the cesium clock. Ordinary quartz timepieces often have a crystal with a frequency of 32.768 kHz. A day has 24 hours, each having 60 minutes of 60 seconds each; 8*4*4 is 128, and so a day may be divided into 128 equal parts of 675 seconds. A quartz clock could gradually add one second to a year by adding one cycle of 1/32,768 second to a second every 675 seconds for the first 256 days of the year.
If we were to view spreading the extra second evenly over the first 360 days of the year as the theoretical ideal, and the scheme described for the cesium clock of adding 294 of its cycles to the second for the first 31,267,455 seconds of the year, or the first 361 days and 77,055 seconds of the year, as an approximation to it, then a closer approximation for a quartz timepiece would be to add one cycle of 1/32,768 second every 949 seconds for the first 359 days and 79,232 seconds of the year.
As for rubidium clocks, they use Rubidium-87, just as the cesium clock uses Cesium-133; for them, the number of cycles in a second is 6,834,682,612.8 for the microwave radiation caused by the hyperfine transition within what would otherwise be its ground state. The closest approach to adding one second in 360 days would be 219.8 such cycles, but that doesn't divide the second evenly, so we would have a number of long seconds, and then one intermediate second before returning to the SI second.
Assuming we want to stick with a clock multiplier of no more than 5, we need to factor 34,173,413,064. It is 8 * 9 * 7 * 23 * 983 * 2999, and from these factors, we want to make a number close to 1,099 (or 219.8 times 5). We can't choose 983 as our approximation, as it would take more days than there are in a year for 194.2 rubidium cycles a second to make an extra second; 8*9*7 is 504, so our approximation must be a multiple of 23. 1,099 divided by 23 is 47.7826..., and we're short one factor of two to make 48, and one factor of seven to make 49. For that matter, we're short a factor of 23 to make 46, and even short a factor of 3 to make 54.
So, if we choose 56 as the closest higher approximation, 8 * 7 * 23 is 1,288, so we are adding 257.6 rubidium cycles to the second for the first 26,532,153 seconds of the year, or the first 307 days and 7,353 seconds. So with our best even approximation, we revert to the SI second about two months earlier.
In the case of the quartz approximation, since 1/32,768 second was much larger than the 31.7 or so nanoseconds we wished to add, we simply added one such cycle every 949 seconds. Here, to pad out 307 days to something closer to 360 days, we could alternate six modified seconds, to which a multiple of 257.6 rubidium cycles were added or subtracted, with one unmodified second through the first part of the year. Of course, since 7,353 isn't divisible by six, one doesn't end up with an integer number of cycles, but the seconds still come out even, with three modified seconds after the last unmodified second in the first part of the year, which now comprises 358 days and 22,978 seconds (including those last three odd modified seconds).
At first, I thought that perhaps the Cesium version of civil time should be made the official standard. However, after further thought, I now think that the official standard for civil time should be the one where any leap seconds are spread evenly over the first 360 days of the year.
Because the reversion to SI seconds comes less than 2 days before the 360 day mark for reversion in the nominal civil time for this form of Rubidium civil time, and the reversion is less than 2 days late for Cesium civil time as described, the two scales are, at their worst, within 1/90th of a second of each other, and within 1/180th of a second of nominal civil time. For most applications where such an accuracy is not satisfactory, some form of atomic time with SI seconds only, with or without leap seconds, can be used.
Since either a rubidium or cesium oscillator provided with supplementary circuitry to produce civil time would also, more easily, produce SI seconds as well, such an oscillator could be calibrated using SI seconds. Even if the simplistic notion of adding even multiples of 257.6 rubidium cycles to the second was retained, if the insertion of SI seconds followed a more sophisticated rule, a rubidium oscillator could be used to provide a clock that was, during a year with only one leap second, always nominally within 32 nanoseconds of nominal civil time; such precision, however, exceeds the accuracy actually available from any clock.
One way to perhaps more clearly understand what I am advocating is this:
The first change that I envisage to present timekeeping would be to modify UTC so that:
In a year with one leap second, that leap second would always be added at midnight June 30th; in a year with two leap seconds, those leap seconds would always be added at midnight March 31st and midnight September 31st; in a year with three leap seconds, those leap seconds would always be added at midnight February 28th (February 29th in leap years), June 30th, and October 31st.
The number of leap seconds in a given year would be announced prior to the beginning of the preceding year.
These two changes would mean that this direct replacement for UTC would no longer always be within 0.9 seconds of mean solar time, but instead that the allowable divergence would be somewhat larger.
Some applications that require very high precision in timekeeping and which require a constant length of the second, but which also require to be tied closely to mean solar time would use this time scale.
Other applications, requiring very high precision in timekeeping and a constant second, but which are intolerant of the difficulties involved in applying leap seconds, could simply use plain TAI or GPS time.
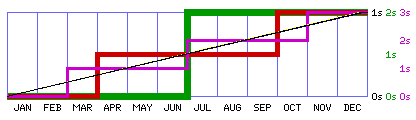
The diagram below shows a dark green line indicating the step of adding one leap second on June 30th, and a red line showing the two steps of adding one of two leap seconds, and a purple line showing the three steps of adding one of three leap seconds at a time.

Because I believe there is a broad and important class of timekeeping applications where a small change in the length of the second can be tolerated, but where neither the inconvenience of adding leap seconds, nor the prospect of getting out of sync with the mean solar day, can be accepted, the time scale I advocate here, illustrated by the black diagonal line in the diagram involves a second that is made slightly longer (32.15020576... nanoseconds, in the case of a year with one leap second) for the first 360 days of the year. It is flanked by a yellow line and a light green line representing the Rubidium and Cesium simple approximations to nominal civil time.
Note that while in decimal notation, the civil second becomes 1.00000003215020576... seconds, in sexagesimal notation it comes out even:
Start with a second
1
Add a leap second
2
But the added leap second is split between the first 360 days of the year
1:00:10
And the twenty-four hours of every day
1:00:00:25
And the sixty minutes of every hour
1:00:00:00:25
And the sixty seconds of every minute
1:00:00:00:00:25
In this way, while the convenience of the old system, where an approximation to mean solar time was directly used as civil time, is retained. But instead of a second that can change in length in an arbitrary manner which is difficult to even describe, a time scale is used that is still directly tied to atomic time.
Thus, in the civil time standard I propose, one is basically formalizing the practice of letting one's clock run a little bit slow in order to blur the leap second out of existence. Thus, as existing applications that had been ignoring the leap second, because it was irrelevant for the level of timekeeping precision involved in these applications, have, due to advances in technology, an increased requirement for timekeeping precision, a time scale would be available that, because it is strictly and simply defined in terms of atomic time, allows any desired level of timekeeping precision to be maintained, while also painlessly maintaining both the absence of the leap second, and continued close correspondence to the normal time of day.
It might also be asked why this scheme provides the original benefit claimed for it. After all, isn't it just as easy to forget to push the button on your fancy rubidium clock that tells it that this is a year with a leap second as it is to forget to add the leap second?
And the answer is that my scheme does reduce the chances for chaos in two ways.
For one thing, instead of being out by one second at the moment that the leap second passes by, if a mistake is made, the time discrepancy now gradually accumulates over the course of the entire year, so it might produce minor problems, and be noticed, before it gets large enough to cause major problems.
But more importantly, most people don't have fancy rubidium clocks. They have ordinary quartz clocks, and, for applications requiring time synchronization to less than a second, they have to periodically reset their clocks based on a time standard. If they use a time standard providing the kind of civil time I propose, this also takes care of the leap second issue automatically. If explicit leap seconds are used, however, then even people with clocks whose intrinsic accuracy is poorer than one second a year have to remember to adjust their clocks for leap seconds in addition to the unavoidable requirement of keeping them in step with the correct time by reference to a time signal from someone with a more accurate clock.
So the chief benefit of this proposal is that it vastly reduces the number of people who have the opportunity to make mistakes involving leap seconds.
Of course, many modifications of this scheme are possible from which to derive other schemes based on the same general principles. For example, the idea of making the amount added to the second an even number in the sexagesimal system may not be felt to make sense. To add a leap second in the course of a year, the length of a second has to be increased by just over 31.7 nanoseconds at least. So, another scheme might work like this:
To more closely approximate the normal second of mean solar time, and to keep everything to normal steps, normally use a second that is 16 nanoseconds (rather than 15 nanoseconds) longer than the SI second. If this is also done only for the first 31,250,000 seconds of the year (365 days having 31,536,000 seconds), reverting to the SI second after, then during the time when the SI second is used, we would, in alternate years, have seconds that are out of phase with TAI, differing by an offset ending in 0.5 seconds. When a positive leap second is still required, despite this frequency offset, add a further 32 nanoseconds to the second, giving a second that is 48 nanoseconds longer than the SI second; a negative leap second, which in this system is more likely to be needed on occasion, could be achieved by subtracting 32 nanoseconds, giving a second that is 16 nanoseconds shorter than the SI second.
Another option, which avoids frequency offsets altogether, but still obtains a similar effect, would be this: use the SI second, but, in a year with one leap second, every 8 hours for the first 333 1/3 days of the year, lengthen one second by one millisecond.
Thus: in any year having a nonzero number of leap seconds, lengthen (or shorten, as the case may be) the following seconds in each of the first 333 days of the year by as many milliseconds as there are leap seconds required: 7:59:59, 15:59:59, and 23:59:59. On the 334th day of the year, November 30 (or November 29 in leap years), do the same only to 7:59:59.
This would allow a single time standard, since time signals for most of the day would consist of a steady stream of SI seconds, suitable for calibrating frequencies.
An even simpler thing to do to add one second to the year would be simply to add 4 milliseconds to one of the seconds in a day, presumably the one at 23h 59m 59s Greenwich Mean Time, for the first 250 days of the year.
This scheme raises another point. Prior to the adoption of the current UTC system in 1972, the goal had been to keep UTC within one-tenth of a second of mean solar time, as this was felt to be required for applications related to astronomy and celestial navigation. If the scheme of timekeeping is to be changed once again, in order to get rid of the leap second for the convenience of operators of computer networks, it might be asked if there is also an opportunity to meet the needs of this user community more fully once again. At the present time, while UTC is only kept within 0.9s of mean solar time, broadcast time signals all include the difference between UTC and UT1 to the required precision of one-tenth of a second.
One way of doing that might be this:
Divide the year into 10 parts, alternating at 37 and 36 days in length. To keep things simple, let's start with March 1st. This gives us ten periods whose start days are:
March 1 (37) April 7 (36) May 13 (37) June 19 (36) July 25 (37) August 31 (36) October 6 (37) November 12 (36) December 18 (37) January 24 (36, 37 in leap years)
and we sweep a leap 100 milliseconds under the rug now by inserting it, one millisecond at a time, in the last second of every eight hours for the first 33 1/3 days of each of those periods.
And here's a little calendar
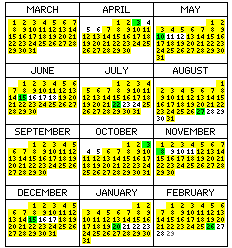
that shows the days with three leap milliseconds with yellow backgrounds, and the ones with one leap millisecond with a green background. Of course, these are actually opportunities for leap milliseconds, and any one block of 33 yellow days followed by one green day may or may not include leap milliseconds, depending on how the time scale is being adjusted that year.
Perhaps life might be less complicated with one leap millisecond every six hours, for the first 25 days of each month, rather than to try to redivide the calendar on the basis of ten slightly longer months in the year.
Further changes in detail are possible. Let us suppose that one leap millisecond every six hours is too often; introducing an irregularity in the second more than once a day causes the time scale to fail to meet the demands of metrology. Then, simply add 4 milliseconds to the first 25 days of each calendar month in which a 100ms advance is needed, the step always taking place at 23:59:59 UT. Or, if 5ms is a better step, make that 5 milliseconds to the first 20 days of the month,
Just as I proposed dividing the year into 10 periods of either 36 or 37 days to allow 33 1/3 days into each of them, with a 5 millisecond step spread over 20 days, one could divide the year into 17 periods, each three weeks in length, with a leftover period of one week and one day (one week and two days in leap years), and add 5ms each day for the first 20 days of each three weeks of the first 51 weeks of the year; if we start on the first day of the year that falls between Tuesday and Friday, the day that does not end in an adjustment will fall from Monday to Thursday, allowing both days of each of the 48-hour streches guaranteed to be without a long (or short) second to be within the work week.
However, this scheme, although it spreads the steps out so as to be invisible to people with ordinary clocks, is otherwise very similar to Stepped Atomic Time, which was a scheme tried shortly before the current UTC system with leap seconds was adopted. It was found in practice that steps of 200 milliseconds, as used in that system, could not be anticipated far enough in advance to make that a usable time scale.