One question that sometimes arises when people think about astronomy is if the planets ever all line up together.
Looking at this from a simplified standpoint, I begin by ignoring the planets Uranus, Neptune, and Pluto. These planets take a very long time to orbit the Sun, and so if we consider them, it would take an extremely long time for all the planets to line up. If we consider only the planets up to Saturn, which were known to the ancients long before the telescope was invented, will even all of those planets ever be lined up together?
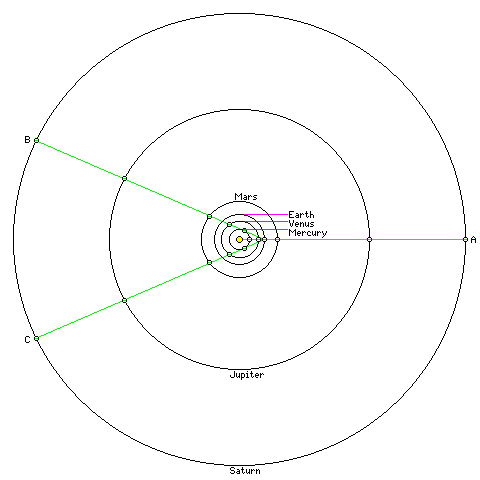
To further simplify matters, let us think of the planets as travelling in perfect circles around the sun, rather than in elliptical orbits, and also ignore the gravitational influence of the planets on each other.
We must still ask another question: what does it mean for all the planets to be lined up?
The line from the Sun to Jupiter at point A shows all the planets in the same direction from the Sun. This is the simplest type of all-planet alignment to consider.
For all the other planets to be clustered together in the night sky, however, they must all be in the same straight line as seen from Earth. Two possible configurations are shown by the lines going from the Sun to Jupiter at points B and C.
Mercury is shown as being as far from the Sun as it is possible to get from our perspective; this position is called maximum elongation. Venus has two possible positions in its orbit that intersect each of the lines.
The line going to C represents a cluster visible in the early evening, and the line going to B represents a cluster visible before dawn.
The diagram is not to scale, it should be noted.
For the planets to repeat any configuration, however, is similar, if their periods are not synchronized so that some configurations are impossible, to them coming into the alignment represented by the line going to A. The important thing to note is simply that a gathering of all the planets in the sky can occur in four possible ways, not just one.
How closely together the planets are required to come to each other also affects how often the condition will be met.
One way to start looking at this problem is to begin with the two slowest-moving planets among the ones under consideration, Jupiter and Saturn.
Saturn takes about 30 years to orbit the Sun, and Jupiter takes about 12 years to orbit the Sun. Jupiter and Saturn by themselves, then, will both be in the same direction from the Sun at regular intervals; about every 20 years, Jupiter will have orbited the Sun once and then advanced far enough ahead to catch up with the slower-moving Saturn.
More precisely, the interval between such encounters is 7253.6281 days, a little over 19 years and ten months. And in that time, Jupiter and Saturn will be displaced by 242.7 degrees in their orbits around the Sun. Note that this is close to 240 degrees, two-thirds of a circle; five Jupiter years are very close to three Saturn years. It is also true that eight Venus years are very close to five Earth years. While an exact resonance could make some configurations of planets impossible, approximate ones only mean that the near misses occur close to the closest alignments, with a long period in between of no approximate alignments.
How far will the other planets have moved in this time?
Mercury 164.3037 281.6 ( -78.4) Venus 101.2589 218.5552 (-141.4448) Earth 309.2363 66.5326 Mars 201.1495 318.4358 ( -41.5642) Jupiter 242.7037 Saturn 242.7037
The first column shows how far the planets have moved; the second column shows how far they have moved compared to Jupiter and Saturn.
Starting from any given position relative to each other, then, how many times must Jupiter and Saturn come into alignment for the other planets to return to the same alignment as well?
The number of such conjunctions required is about:
Mercury 4.5918 Venus 2.5452 Earth 5.4109 Mars 8.6613
Thus, if one rounds them down to 4.6, 2.5, 5.4, and 8 2/3, one finds they should repeat their relationships to Jupiter and Saturn in 23, 5, 27, and 26 conjunctions, approximately. Five times five is 25, which is in the same ballpark. However, that is too rough an approximation to hold up over the long period of time that would be required to get a common multiple of all four numbers.
However, it is still interesting to note that 23 times 5 times 27 times 26 is 80,730, and that times the 7253.6281 days between conjunctions is about 1,603,279 years and eight months. The actual time it takes for all the classical naked-eye planets to align will be even longer than this, since it is based on a crude approximation, and including Uranus, Neptune, and Pluto would make it take vastly longer yet.
What relationship do the positions of the planets at a given date, and 4,809,839 years before or since, bear to each other, if any?
To really get an idea of how long it would take for all the planets to align, we need to consider each additional planet to be brought into alignment one at a time.
So, after 26 conjunctions of Jupiter and Saturn, we find the other planets have moved by this amount in degrees:
Mercury 121.6 Venus -77.5648 Earth -70.1524 Mars -0.6692
After three times, Mercury will be in alignment, and Mars still won't be too badly off. After enough times, though, the .669 degree error in the approximation will add up, and so we will have to switch to a closer approximation, making our goal of having the planets repeat themselves recede further into the distance. Even just allowing 36 repetitions of 26 conjunctons lets the error in Mars' position add up to 24 degrees. That suggests itself as a period from the appearance of the numbers presented, and is only 18,588 years and nine months, or 6,789,395.9 days. Do the planets even approximately repeat themselves in that time, or in fifteen such periods?
Even 18,588 years is much longer than all recorded history.
Because it takes 20 years between conjunctions of Jupiter and Saturn, however, an approximate conjunction remains in effect for a period of time.
Could one view the problem from another perspective, simply treating the planets' positions as random, and considering how often the planets might line up based on how closely one wants them to do so?
To try searching for combinations by a brute-force method, one way to start would be to look at the problem from a perspective centered on Saturn, the slowest-moving planet under consideration.
This diagram makes it obvious what we must look for.
When Jupiter and Saturn are approximately in the same direction from the Sun, we then ask the following questions in order:
Will Mars also be in the same direction approximately?
Will Earth either be in the same direction, or the opposite direction?
Depending on how Earth is situated, if there is still a possibility, knowing what type of possibility it is then tells us where Venus and Mercury should be.
Note that there are many other possibilities as well, if we allow Mercury to be closer to the Sun from our viewpoint. Even an impressive line-up of planets that we can't see in the sky is still of interest.
Now things become clearer. It takes about 26 conjunctions between Jupiter and Saturn for Mars to also be in its most appropriate position. So every 26 conjunctions, or about every 516 years, we have an opportunity, and the chance that the other planets are aligned can be treated as though the positions of those planets are random. Every so often, because the relationship between the period of Mars and the time between Jupiter-Saturn conjunctions is not exact, the time between opportunities will slip.
A page on the web site of the Griffith Observatory (in Los Angeles) notes, among other things, that a very close alignment of the naked-eye planets took place on February 27th, 1953 B.C., in which these five planets were together in a span of 4.3 degrees. No closer alignment has taken place since then: on September 8th of 2040, a fairly close alignment within a space of 9.3 degrees will be observed.