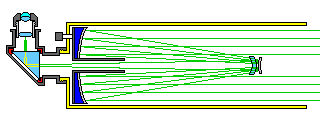
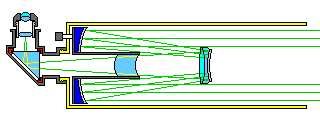
The following illustration:

shows how the large meniscus of the Maksutov design might be replaced by a small meniscus lens just behind the Cassegrain secondary, where light passes through it twice, as in a design by the Australian amateur astronomer Ralph W. Field, and also as seen in the Vixen VMC 200l. A similar plan, but using two elements rather than one is employed in some designs offered commercially by the Novosibirsk Instrument-Making Plant of Russia, as illustrated below.
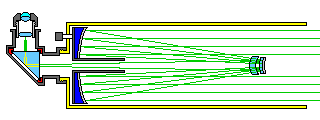
This telescope design is due to Klevtsov, and another design of this type is due to Argunov.
Recently, the Cape Newise telescope illustrates another method of correcting for a spherical primary:
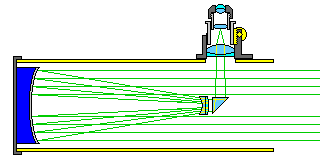
a concave lens allows a small central obstruction, and then a convex lens allows a fast focal ratio, in a telescope which generally follows the basic plan of a Newtonian telescope. Not shown in the diagram is a flat optical window at the front of the telescope used to suspend the concave lens and the diagonal prism, similar to that used in the Astroscan telescope by Edmund Scientific. Note that the two correcting lenses used in the design are both achromats.
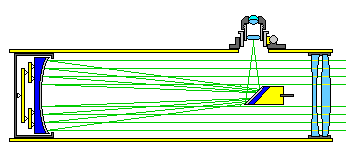
Another unique telescope design is that of the Clavius telescope which is a Cassegrain design that starts with a spherical primary and secondary, and achieves a small central obstruction by allowing an image to form about halfway down the telescope tube. A relay lens system which forms the image magnified by the eyepiece also corrects for the aberrations of the primary and secondary.
Donald Dilworth, an optical designer who will be mentioned in the later section on eyepieces, designed an all-spherical telescope which used a Mangin mirror as the secondary, and which had an arrangement of lenses in the baffle tube resembling a Wynne coma corrector. However, they do have something else to do as well; the image is formed within the baffle tube, and so those lenses also function as a relay lens group. This design was described in the November and December 1977 issues of Sky and Telescope. I suspect its optical performance, like that of his eyepiece design, is superlative.
A popular design of late is the Corrected Dall-Kirkham:
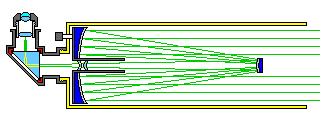
The spherical secondary in this design simplifies aligning the secondary, since it only needs to be positioned correctly, not both positioned and oriented exactly.
The illustrative design is not to scale; as with the Ritchey-Chrètien and the Lurie-Houghton, a large secondary is required by this design, restricting it to photographic use. The advantage of this design is that other aberrations can be corrected in addition to coma, leading to sharp images over a large flat field. Accessory field flatteners are also available for other telescope types, it should be noted, in fairness.
Examples of this design include the CDK series of telescopes from Planewave Instruments, the Ceravolo 300 Astrograph, and the Celestron C20.
A closely-related design was made available by Starizona, the Harmer-Wynne telescope from Starizona. This also includes correcting lenses. Like a Dall-Kirkham, the secondary mirror is spherical. But the primary mirror, instead of being ellipsoidal, is parabolic, so the correcting lenses, in addition to correcting for other abberrations, also take on part of the burden of correcting for spherical abberration.
Many other arrangements of correcting lenses in reflecting telescopes are known; for example, one elaborate one is noted in U. S. Patent 3,180,217, of Argyle and Parker, for the following system with a spherical primary mirror:
which, with a large central obstruction, provides a fast f/4 telescope.
At the exit of the telescope tube, however, other kinds of corrector lenses, such as coma correctors or focal reducers are also used, so I am not certain if a particular brand of inexpensive telescope with an achromatic two-element lens in that position uses it to correct for a spherical primary mirror or not.
A three-element lens combination for correcting coma in a Newtonian telescope with a parabolic mirror, invented by noted optical designer Charles Gorrie Wynne, is often used at observatories; a very recent patent, U. S. Patent 4,718,753, covers telescopes with parabolic mirrors using a one- or two- element coma corrector.
The Gregorian reflecting telescope was designed by one James Gregory in 1663. The particular form of the Maksutov-Cassegrain telescope in which the secondary is created by placing an aluminized circular area on the corrector, to simplify construction, was designed by one John Gregory, during the decade of the 1950s. Hence, the most popular form of Maksutov-Cassegrain telescope is also referred to as a Gregory-Maksutov telescope, although it most definitely is not a Maksutov-Gregorian telescope. It is important not to allow oneself to be confused by this difficulty in telescope nomenclature.
Incidentally, when an aluminized spot on the corrector is used as the secondary mirror, it is necessary to deviate from the spherical symmetry of the basic design in order to correct aberrations more effectively, and to avoid a secondary mirror with an unreasonably long focal length.
The Schmidt camera design and the basic Maksutov design both exploit the symmetry of the spherical primary mirror as a means of allowing off-axis rays to be focused correctly. The usual Schmidt-Cassegrain and Maksutov-Cassegrain telescopes encountered, however, no longer retain this symmetry. The Schmidt-Cassegrain telescope gives it up so that the secondary can be located on the corrector plate, rather than somewhat closer to the primary than to the corrector plate, thus avoiding the need for vanes holding the secondary that obstruct light. The Maksutov-Cassegrain often has a secondary that is an aluminized spot on the corrector plate; in a spherically symmetric design, that spot would simply reflect the light back out of the telescope, and so the corrector plate has to have a steeper curve.
Even without changes in overall design, the fact of having a Cassegrain secondary means the design is no longer spherically symmetric.
Among the several modified versions of the purely catoptric Cassegrain design we examined, the Pressmann-Camichel design gave the poorest off-axis performance; eliminating coma required going in the opposite direction, to the Ritchey-Chrètien design. Given that off-axis performance is already compromised in the common catadioptric Cassegrains, the idea of a Maksutov-Pressmann-Camichel design where a meniscus corrector of reduced thickness is combined with an ellipsoidal secondary to provide part of the correction for spherical aberration may not be entirely preposterous. Actually, though, existing Schmidt-Cassegrain and Maksutov-Cassegrain telescopes are already making use of that principle in a sense; their secondaries are spherical, and as we saw above, the spherical secondary of the Dall-Kirkham design compensates for an undercorrected primary: a fully-corrected primary would require the hyperboloidal secondary of the classical Cassegrain.
Thus, while the symmetry principles illustrated above for the original Schmidt and Maksutov designs are of historical interest, it would be misleading to conclude that Schmidt-Cassegrain or even Maksutov-Cassegrain telescopes are highly corrected against coma. Some Maksutov-Cassegrain designs are better than others in this respect; having the secondary mirror an aluminized spot on the corrector is one thing that involves a compromise; but the compromise is still a minor one, and such telescopes do deserve their good reputation. Instead, for that one needs to consider a telescope based on the Ritchey-Chrètien design.
The Maksutov telescope, whether Maksutov-Newtonian or Maksutov-Cassegrain, is one example of a telescope that can be well-corrected and yet use only spherical surfaces. Another possible design is the Lurie-Houghton telescope:
At first, this design looks like it offers the worst of both worlds; a doublet lens as the objective, and a mirror as well, so one is paying for the optics of both a Newtonian and a refractor. However, the main mirror is now spherical, not parabolic, and the corrector is made from two lenses both of plain crown glass, so one does not need to use flint glass. Also, even after this is recognized, it might be asked what advantage such a telescope has over a Maksutov-Newtonian, which requires just one corrector element, also with two spherical surfaces.
But for an amateur telescope maker, creating two corrector elements that are relatively thin lenses, rather than the steeply-curved meniscus of a Maksutov design, avoids the need to either work from a very thick piece of glass, and remove a lot of material, or somehow find a blank that has already been molded into an approximation of the desired shape.
In addition, the additional lens does allow an additional correction, for curvature of field. Remember, a Maksutov-Newtonian is essentially equivalent to the original Maksutov camera, which like the Schmidt camera avoids coma by being spherically symmetrical everywhere, including the surface on which the image is produced. As a result, a number of amateur astronomers have made themselves telescopes of this type, with focal ratios of f/5 or f/4. Of course, simple Newtonians with very fast focal ratios have been used as well, despite the coma, which can be corrected with commercial attachments at the eyepiece end of the telescope.
One of the best pages on the Web about the Lurie-Houghton telescope is this page by Rick Scott.
One problem with both the Lurie-Houghton and Ritchey-Chrètien designs is that, while they offer the opportunity for very thorough correction of aberrations, they are primarily suitable to short-focus designs with a large central obstruction. Had it not been for this limitation, one or both of these designs might have become much more common and popular.
Since the above was written, innovative optical designs are now being offered by the major vendors of telescopes to amateur observers, so one does not have to go to great expense importing a telescope to improve on the performance of the basic Schmidt-Cassegrain telescope.
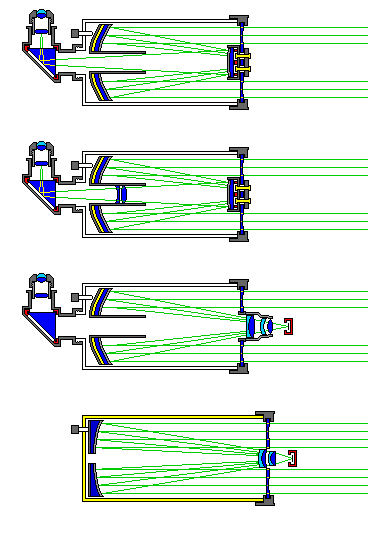
Four new designs are illustrated in the image above.
The top diagram looks just like an ordinary Schmidt-Cassegrain, as I can't illustrate the differences at the scale of these diagrams. But in this case, I'm using the image to represent Meade's new Advanced Coma-Free telescope. The difference between it and a normal Schmidt-Cassegrain is that the Schmidt corrector over-corrects for the spherical primary, with the design of the secondary adjusted to compensate.
This is done to an extent that removes coma from the design, in much the same way as the hyperboloidal primary mirror in a Ritchey-Chretien telescope leads to a coma-free design.
The second diagram shows how Celestron responded to this innovation from Meade.
In Celestron's EdgeHD telescopes, a correcting lens in the baffle tube corrects for both coma and curvature of field.
In the third diagram, we see the Hyperstar accessory offered by Starizona for Celestron Schmidt-Cassegrain telescopes.
Celestron offers a feature, called Fastar, for its Schmidt-Cassegrain telescopes that allows the secondary mirror to be removed, from outside of the telescope, so that a camera can be mounted on the front of the telescope. In this way, the telescope has a faster focal ratio, allowing for wider fields and faster exposures.
The Hyperstar accessory provides correcting lenses that provide an improved image for a camera in this position.
The fourth image illustrates how Celestron has produced a telescope designed solely for astrophotography on a similar principle, the Rowe-Ackermann telescope.
Thus there are very accessible options now for amateur astronomers looking for an advanced design that improves image quality.
One design I haven't seen among the various designs offered, though, is this:
To save money in manufacturing the telescope, it would be desirable if both the primary and secondary mirrors could be spherical.
To allow the use of a spherical secondary, adjust the Schmidt corrector of the telescope so that it makes the telescope behave like a Dall-Kirkham, in the same way that the corrector of a Meade ACF is adjusted to make it behave like a Ritchey-Chretien.
Then add a corrector for the coma in the Dall-Kirkham design, similar to what is used in the corrected Dall-Kirkham. That way, the result would be a telescope with a high-quality optical design, but the front would be closed like that of a Schmidt-Cassegrain.
While an open front for a telescope allows it to cool down more quickly, the closed-front design of Schmidt-Cassegrain and Maksutov telescopes is attractive to many amateur astronomers, as it appears to have safety and maintenance advantages.
Various arrangements to correct for either a parabolic mirror or a spherical one have been developed over time, some even including a Mangin-mirror primary (where the back surface of a meniscus lens is silvered, so that the glass in front of the reflecting surface acts as a lens). One such telescope is the Super-Schupmann design, in which a Mangin mirror corrects the chromatic aberration of a simple crown lens used as the objective:
It is, however, possible using just two spherical mirrors, with no other correcting lenses at all, to provide a design corrected for both spherical aberration and coma; the Schwarzschild microscope objective illustrates this:
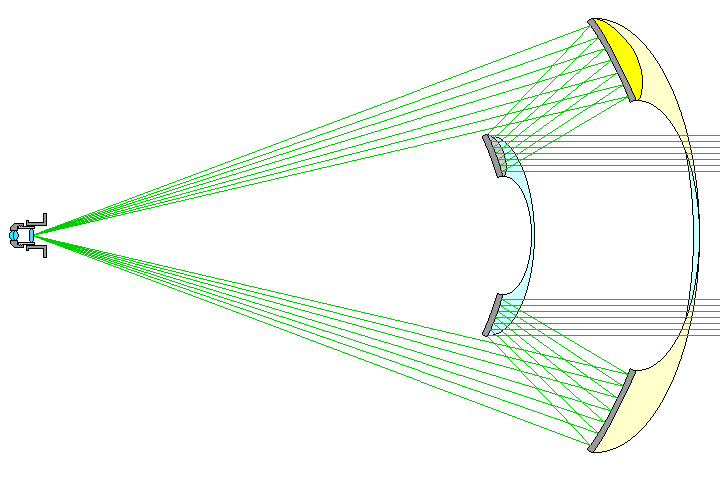
The design, essentially a Cassegrain telescope turned backwards, has an enormous central obstruction. But if one replaces the annular mirrors used in the microscope objective by small circular mirrors, one can get a telescope design with no central obstruction.
Of course, while coma and spherical aberration are corrected, other aberrations exist, and their magnitude in this off-axis design would be characteristic of the large, steep circular mirrors of the original microscope objective, not the size of the mirrors used in the off-axis telescope. An even more serious reason why this type of telescope is usually considered impractical is that the aperture is defined by the smaller mirror, and is thus about half the size of the larger mirror. Another difficulty such a design would pose is that the light entering the eyepiece is all coming from one side; this makes demands on the field lens of the eyepiece that not all eyepiece designs can meet. Also, it would require a long tube.
Of course, the very simplest type of off-axis telescope would be one that simply used a single tilted mirror:

William Herschel constructed an f/10 telescope with a 48-inch parabolic mirror tilted in such a fashion. His reason for doing so was that placing the observer in the light path would create an unacceptable central obstruction with a 48-inch telescope (unlike the 200-inch telescope on Mount Palomar that came later), and that the speculum metal mirrors of his time had only 60% reflectivity, so eliminating the diagonal mirror from the telescope was helpful.
When a parabolic mirror is used and tilted, the telescope is called a Herschelian telescope.
When a parabolic mirror is used, but is formed into a shape approximating an off-axis paraboloid by deforming it mechanically, the resulting telescope is called a Yolo.
Actually grinding an off-axis paraboloid produces an off-axis Newtonian. Alternatively, if the telescope has a long enough focus that a spherical mirror is acceptable, an off-axis Newtonian is also the result. (It may also be noted that the fact that the Maksutov telescope uses only spherical surfaces has been taken advantage of by at least one amateur astronomer, who constructed an off-axis Maksutov telescope.)
When can the mirror in a Newtonian telescope be spherical?
The mirror in a 4" f/10 telescope is almost always spherical, and the mirror in a 6" f/8 telescope needs to be paraboloidal.
For a given level of optical quality, the f-number at which a spherical surface is acceptable grows as the cube root of the aperture. Thus, the following table shows the aperture at which a spherical mirror would be as satisfactory as the spherical mirror in a 4" f/10 telescope, and the aperture at which a parabolic mirror is as necessary as in a 6" f/8 telescope, for some f/ratios:
Focal Ratio Spherical Aperture Parabolic Aperture f/8 2.048" 51mm 6" 150mm f/9 2.916" 73mm 8.5" 214mm f/10 4" 100mm 11.7" 293mm f/11 5.324" 133mm 15.6" 390mm f/12 6.912" 173mm 20.25" 506mm f/12.5 7.8125" 195mm 22.9" 572mm f/13 8.788" 220mm 25.7" 644mm f/14 10.976" 274mm 32.2" 804mm f/15 13.5" 338mm 39.6" 989mm f/16 16.384" 410mm 48" 1200mm f/17 19.652" 491mm 57.6" 1439mm f/18 23.328" 583mm 68.3" 1709mm f/19 27.436" 686mm 80.4" 2009mm f/20 32" 800mm 93.8" 2344mm f/24 55.296" 1382mm 162" 4050mm f/30 108" 2700mm 316" 7910mm
Note that this table uses the conventional conversion of 25mm to the inch instead of the exact 25.4mm to the inch.
Note also that, because aperture goes as the cube of the focal ratio, instead of an f/10 4" telescope and an f/8 6" telescope being close together, the distance between these two limits is actually a factor of three.
For more insight into whether a telescope between the limits shown here can have a spherical or a parabolic mirror, in the case of a telescope with an f/10 focal ratio, the degree to which a spherical mirror approximates an ideal mirror for various apertures is shown in the following table:
Quality Aperture 1/4 wave 11.196" 1/8 wave 5.574" 1/16 wave 2.468"
Compared to the limits above of 4" and 11.7" for the f/10 focal ratio, then, we can say that using an aperture up to 1.39 times the spherical aperture shown above should definitely be acceptable, giving 1/8-wave quality, and using an aperture up to 0.95 times the parabolic aperture shown above will give at least 1/4-wave quality.
Thus, one can obtain an off-axis Newtonian by using a tilted spherical mirror with a sufficiently long focal length as to form part of the larger spherical mirror in a conventional centered Newtonian which could use a spherical mirror. Thus, tilting a 10" f/36 spherical mirror, which would be a portion of a larger spherical mirror with a 360" focal length and a diameter of perhaps 22 inches would produce acceptable results.
Another popular off-axis telescope type is the Schiefspeigler:
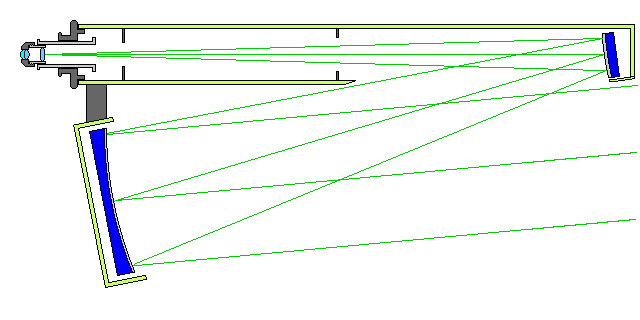
which offers a large unobstructed aperture with only slightly more bulk than a refractor of much smaller aperture, and which can be made with only spherical surfaces provided the focal ratio is somewhat long.
Although this is an exotic design, which was new to many amateurs when a relatively recent article in an astronomy magazine discussed it, it has been known for some time; the illustration below:
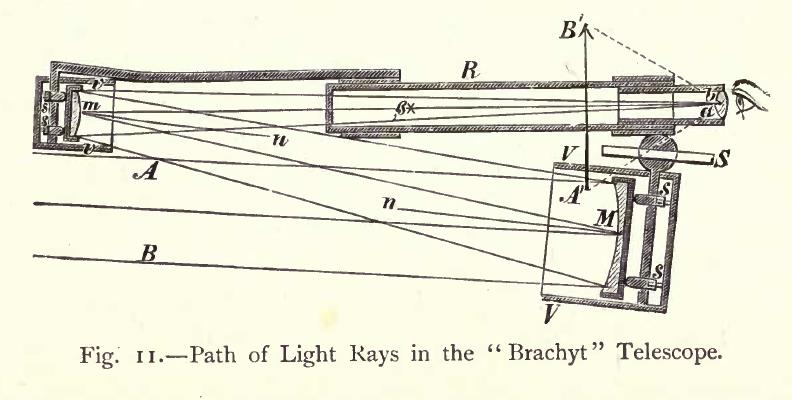
came from the book "The Amateur Astronomer" from 1910.
As can be seen from the image, another name for this type of telescope is the brachyt, which is often contrasted with another related type, the medial telescope, of which the Super-Schupmann above is an elaboration.
Considering such designs as the Schmidt, the Maksutov, and the Super-Schmidt, as well as the possibilities for economizing on the size and cost of the corrector illustrated by the Field telescope, had made me wonder why no one has ever designed a telescope like this:
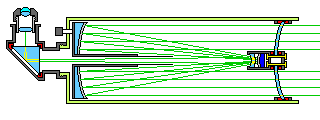
where a thin meniscus with a shallow curve provides a small amount of correction for spherical aberration, but primarily serves as a place on which to brace a Cassegrain mirror of a convenient focal length, with most of the correction for the spherical shape of the primary coming from a corrector of the type used in the Field-Maksutov telescope. I felt that it would be more satisfying to the general consumer, and not only to my own personal tastes, if, when one adds a piece of glass to the telescope to hold the secondary in place (thus avoiding diffraction spikes), one uses that element in some way to reduce aberrations as well rather than having an optical flat in the position.
I had felt that this kind of design would allow an economical telescope to be made with sealed-tube construction. However, a telescope of this kind could not be as short as a conventional Schmidt-Cassegrain telescope, because with steep curvatures, limitations of this type of corrector would become apparent.
In attempting to work out an actual design of this type, I obtained one with a larger central obstruction than I was hoping for, but still a design many amateur astronomers might find useful. However, the full-aperture corrector, instead of being curved in the same direction as that of a Maksutov telescope, was curved in the opposite direction. Here is the design I obtained, using BK7 glass for both glass elements:
Radius of Thickness/ Radius of Curvature Separation Aperture 414.146 5 BK7 Full-aperture corrector 104 402.814 300 air (exit surface) 104 -810.947 -265 air Primary mirror 100.49 94.669 -10.935 BK7 Field corrector 40.5 96.045 -1.5 air (exit surface) 40.5 -397.620 1.5 air Secondary mirror 39 96.045 10.935 BK7 Field corrector (second trip) 40.5 94.669 458.944 air exit from field corrector 40.5
I had wondered why the full-aperture corrector, arbitrarily chosen to be 5mm thick for a nominal 200mm diameter aperture (or 8-inch) telescope (with an f/13.9 focal ratio) was reversed in direction. However, U. S. Patent 2,726,574 illustrates a mirror lens design, produced by noted optical designer W. Mandler for Leica's Canadian operations, which uses only a single type of glass, and consists of a classic Maksutov design with a reversed corrector in front of the meniscus corrector, as well as an additional two lenses at the exit from the lens, in the traditional coma corrector position. If a standard Maksutov telescope can benefit from a reversed corrector, then it is not surprising that a Field-Maksutov design might do so too.
While the full-aperture corrector is thin, the design failed to meet one of my goals for the design, that it would have a shallower curve than the primary mirror, in order to make the telescope described here extremely economical to manufacture. Reducing the curvature from its optimal value, however, doesn't seem impossible, as that would produce a design intermediate between this design and a plain Field-Maksutov, sealed with an optical flat.
The basic limitation of the Field-Maksutov telescope, as well as the Pressman-Camichel telescope, is this: as you get closer and closer to the focus of a spherical mirror, you approach the point where the rays of light that reflected from the outer portions of the mirror, instead of merely heading in a slightly incorrect direction towards the focus, are wrongly directed by a more significant amount. As this happens, higher-order spherical aberrations become important. Therefore, these designs do not allow one to reduce the size of the central obstruction as much as might be desired. A full-aperture corrector, as in a Maksutov telescope, avoids this limitation.
If one considers the Field-Maksutov telescope as analogous to the Pressman-Camichel telescope, performing all the correction for spherical aberration at the secondary, and the conventional Maksutov-Cassegrain telescope as analogous to the Dall-Kirkham telescope, which performs all the correction for spherical aberration at the primary, then one might not be surprised that by having a full-aperture corrector as well as one at the secondary, one might choose to distribute the correction for spherical aberration between them to also correct for coma - the same principle used in choosing the nature of the two aspheric surfaces in the Ritchey-Chrètien telescope. This might permit a telescope with all spherical surfaces that could be made inexpensively to offer an optical performance rivalling that of the novel catadioptric design from Meade which modifies the Schmidt-Cassegrain, appearing in first the RCX400 and then the LX200R. (Of course, Maksutov designs, with their thick correctors, generally are felt to have cooling and weight problems that limit them to smaller apertures.)
However, the required distribution of correction for spherical aberration to correct for coma, despite the analogy with two-mirror designs with aspheric surfaces, may not be the same. Thus, Astro-Physics once sold a Maksutov-Cassegrain telescope of 10-inch aperture and f/14.6 focal ratio, regrettably since discontinued, that was corrected for coma by having an ellipsoidal primary mirror: the corrector had spherical surfaces, and the secondary was an aluminized circle on the corrector.
Also, while many descriptions of the Schmidt-Cassegrain telescope give it a spherical primary and secondary, this is not true of all commercial products. For example, some models of Celestron Schmidt-Cassegrain telescopes allow the use of an accessory CCD camera (sold under the Fastar trademark) which replaces the secondary mirror, turning the telescope into an f/2 camera. The attachment includes corrective lenses, because the secondary mirror remains spherical; the manuals note that this mirror is hand-figured, but this apparently is to ensure its quality and the accuracy of the focal length, not to aspherize it, as I originally thought.
Closely related is the Wright camera; this modification of the Schmidt camera places the corrector at the focal plane, instead of the center of curvature, and makes the primary aspheric to correct for coma; of course, this design could also be used to produce a Wright-Newtonian telescope.
Another design that corrects for coma is the aplanatic Gregorian telescope; this design does not require the hyperboloidal surfaces, which were considered difficult to test, that led to amateurs making Dall-Kirkham telescopes instead of classical Cassegrains or Ritchey-Chrétien telescopes.
Speculations on how the optics of a telescope using only spherical surfaces might be designed have led me in strange directions.
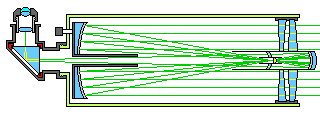
Above, we saw the Fields-Maksutov telescope, which replaced the large meniscus corrector with a small corrector in front of the secondary. However, for this to work, the secondary mirror has to be fairly large, otherwise the secondary and its corrector would have to be too close to the focus, making the spherical aberration too strong to correct easily.
If one's goals include a very small central obstruction, then, it seems that a full-aperture corrector is needed. The Lurie-Houghton design lets one correct for both coma and spherical aberration, which is desirable in a telescope. But Lurie-Houghton-Cassegrain telescopes also have fairly large central obstructions, so, instead, let's correct only for the primary, using a corrector designed for a Lurie-Houghton-Newtonian telescope.
This means the secondary still needs its own corrector. In a Cassegrain telescope, a corrector in front of the secondary has to be bigger than the secondary, because the light is converging as it approaches the secondary. To avoid this, to keep the central obstruction small, one could use a Gregorian telescope design.
Correcting for coma and spherical aberration for the secondary is simple enough; one can use a concentric Maksutov meniscus corrector for the secondary.
Locating it near the prime focus allows a hole to be made in the meniscus so that it acts upon light going in one direction only.
And a baffle tube can be placed in that hole. Lenses can even be put in that baffle tube. One useful thing they could do is correct for the curvature of field that this design, as described so far, would otherwise have. Also, lenses in this area might be useful for temperature compensation: to keep costs down, for a mass-market item, the full-aperture Lurie-Houghton corrector might be made from acrylic plastic instead of glass, which is considerably more sensitive to temperature than glass is, an important consideration for an astronomical telescope often taken out for observing on chilly nights.
Peter Ceravolo designed an all-spherical Gregorian telescope whose only correctors were tiny lenses in the position of this innermost baffle tube. The central obstruction was, of course, a bit on the large side in that design, and the tolerances of the corrector were, of course, critical.
The goal of the kind of design I've sketched above is to provide a telescope that could be made inexpensively (all-spherical optics, possibly even a plastic full-aperture corrector), that would have high optical quality (being corrected for spherical aberration, coma, and curvature of field) and which would appeal to buyers not overly familiar with telescopes (sealed-tube design, therefore no exposed front-surface mirrors; small central obstruction).
Getting rid of the full-aperture corrector, and making the primary mirror a Mangin mirror, so that only glass surfaces were exposed, would be a way of making a telescope that is constructed both to be acceptable to the mass market and to be very light and portable for its aperture, one where there is no telescope tube, and instead only the baffle tube is used to block stray light.
However, the goal of making a "department-store telescope" with an aperture in the 6" to 10" range (150mm to 250mm) and high-quality optics (but having too long a focal length to be the kind of versatile telescope knowledgeable astronomers seek, instead, placing the usual meretricious emphasis on magnification) may be viewed as a rather dubious one.
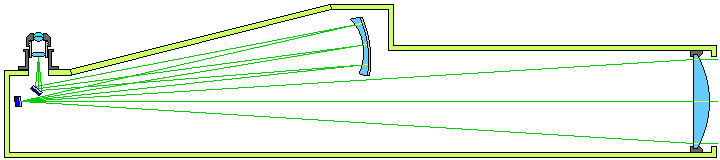
I had at one time toyed with the idea of a telescope design which would offer the following desirable characteristics:
This led me to the design illustrated below:
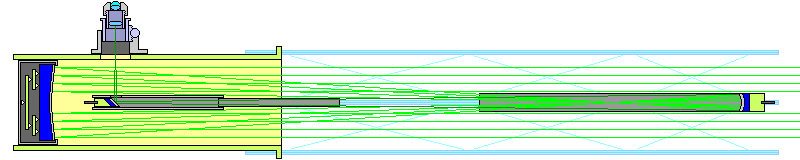
A short tube holds the primary mirror, a tertiary diagonal, and the eyepiece holder. Only one small, light component, the secondary mirror, is a considerable distance away from the primary mirror, and thus it would have to be held rigidly in place by a lightweight structure. Although that is challenging, many professional astronomical telescopes use a structure known as the Serrurier truss which achieves rigidity with very light weight.
The telescope is of the Gregorian type, rather than the Cassegrain type, in order that the secondary mirror might be easy to obtain as a standard component; the distance between the eyepiece and the secondary being so large, in comparison to the width of the secondary, that the error from using a paraboloidal secondary, instead of the appropriate ellipsoidal secondary should be inconsiderable.
Of course, one could avoid that imperfection by making the telescope a Mersenne-Gregorian; let the two mirrors form an afocal telescope, and use a small achromatic or even apochromatic refracting objective at the far end of the baffle tube. Then, moving the secondary out of the way lets the telescope act as its own finder.
A small central obstruction, and an eyepiece located where one does not need a ladder to observe. What could be wrong with this perfect telescope design?
One thing is sacrificed to achieve the merits of this design: flexibility.
Let us say that one uses, as the primary, a 10-inch mirror, with an 80-inch focal length, that is, an f/8 mirror. Since a telescope should cover more than just a single point on the sky, to avoid vignetting, the secondary will be a 2-inch mirror with a 12-inch focal length, an f/6 mirror.
It isn't actually clear that such parts would be available off the shelf; an f/5.6 10-inch mirror, and an f/12 3-inch mirror, for example, would probably be much easier to find, as focal length tends to increase more slowly than aperture for the most popular telescope mirrors; but there is some choice in focal lengths for any given mirror diameter, so it might be possible.
The distance between the primary and secondary would be just slightly longer than 92 inches, so that the light reflected from the secondary would come to a focus, and that focus would be about 92 inches away from the secondary, so that the eyepiece would be in the vicinity of the primary mirror, and near the center of gravity (and hence the pivot) of the telescope.
If one multiplies 80 inches by 92 divided by 12, one obtains 613 1/3 inches as the effective focal length of the resulting telescope. If the distance were instead 96 inches, times the factor by which the distance of the secondary from the focus is greater than its 12 inch focal length, so as to bring the light to the focus, one gets a round 640 inches as the focal length of the telescope.
As it happens, there is a group of photographers known as "f/64", this being a narrow aperture not available on most photographic lenses which provides a very large depth of field, bringing both foreground and background detail into sharp focus.
A telescope with a focal length of 640 inches, if used with an eyepiece having a 40mm focal length, this being approximately 8/5ths of an inch, would provide a magnification of 400x. This is 40x per inch of aperture; in general, the upper limit of usable magnification in a telescope is held to be either 50x per inch or 60x per inch.
As it happens, however, 40mm is about as long a focal length as might be obtained for an eyepiece with a 1 1/4" barrel.
Thus, this particular telescope design is usable for examining the night sky only at magnifications which are at or near the maximum that can possibly be used for a telescope of its aperture.
Thus, my quest for a perfect telescope led, in respect of this design, to a telescope that is almost useless instead.
Placing a positive lens system in front of the tertiary mirror to reduce the effective focal length would improve the flexibility of the instrument, and such a lens could, additionally, be designed to provide some degree of coma correction, as well as allowing the secondary to be placed at the exact location its paraboloidal shape would suit, the one making the primary and secondary an afocal instrument, but here one is wandering into realms of additional complexity.
But with such a design, just move the secondary out of the way, and the telescope becomes its own finder: perhaps sliding the eyepiece and the tertiary mirror to one side would allow this without putting any extra items out where the secondary is, and without increasing the size of the vanes holding the tertiary mirror!
For many years, the world's largest telescope was the famed "Glass Giant of Palomar", the Hale telescope, with an aperture of 200 inches (5 meters).
A Soviet telescope with a 6 meter aperture (236 inches) was later made, but had some operational difficulties.
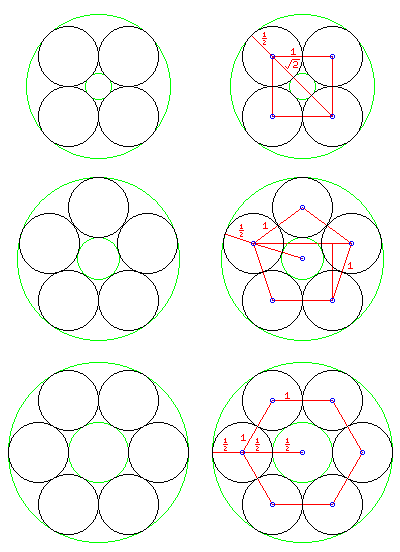
Today, there are many telescopes which use individual mirrors as large as 8.3 meters in diameter (325 inches). Often, such telescopes use more than one mirror in order to achieve even larger apertures. As well, they use the sophisticated technique of adaptive optics in order to deal with the problems presented by the non-uniformity of the Earth's atmosphere.
One way in which several circular mirrors can be combined to make a larger aperture is to arrange seven of them in a hexagonal pattern, as shown in the bottom portion of the illustration at right. This arrangement has actually been used in some telescopes, such as the original Multiple Mirror Telescope.
If we neglect the necessary space between the component mirrors, seven circular mirrors, each assumed to have a diameter of 1, occupy 7/9ths of the area of the circle of area 3 the aperture of which they attempt to match.
All seven mirrors can be identical if the combined mirror is to be spherical; if it is to be a paraboloid, or other aspheric surface, the central mirror is an on-axis one, and the other six mirrors would be of a more difficult off-axis type. Also, depending on the optical arrangement used, it is possible that the central obstruction of the overall system would limit the usefulness of the central mirror.
If we do not use a central mirror, but arrange only six mirrors symmetrically around a central point, then only one-third of the circular aperture is occupied by these mirrors on the periphery. If we compare the occupied area to that of the annulus left by a central obstruction, we have a central obstruction of 33 1/3 percent of the diameter, and 3/4th of the area of the annulus is used.
An advertisement for a Compact Disc changer noted that the arrangement favored for them, of five disks around a center, makes the most efficient use of the bounding circle.
With four circles in a bounding circle, if the circles have diameter 1, as can be seen from the top right corner of the diagram diagram at left, the diameter of the bounding circle is sqrt(2)+1, which leads to about 68.63% occupation of the area of the bounding circle.
The central obstruction has a diameter of sqrt(2)-1, so here we have an annulus deriving from a central obstruction about 17.16% of the overall diameter. The four component mirrors make up 70.71% of the area of the annulus, or 1/sqrt(2) of it.
So we have that for four mirrors, 68.63% of the circle is occupied, while for six mirrors, 66.67% of the circle is occupied. What is the figure for five mirrors?
An arrangement with five mirrors would have two advantages, both deriving from the fact that no space is left for a central mirror. A central obstruction of reasonable size could be present without making that central mirror nearly superfluous, and all the component mirrors of the primary could have an identical off-axis figure.
The component mirrors having a diameter of 1, their centers are the vertices of a pentagon with side 1.
To determine the efficiency of this arrangement, we need to know the radius (and hence the diameter) of the bounding circle. For this, we need to know the distance between the vertices of the unit pentagon and its center.
That would be 1/(2*sin(36°)), and from this we can calculate that the circle is filled with 68.52% efficiency. This is actually less efficient than the case for four mirrors, although more efficient than for six.
In the case of the annulus, which this time has a central obstruction of 25.96% of the aperture, the five mirrors form 73.47% of the area of the annulus, as against 70.71% for four mirrors, and 75% for six mirrors.
So, considering the whole bounding circle, four mirrors are better than five, and considering the annulus only, six mirrors are better than five. Yet, five mirrors don't have quite the same degree of wasted space on the periphery as four, and they don't have the large center hole of six, so despite not having a simple claim to maximum efficiency, they still seem an attractive alternative.
Instead of simply evaluating the sine of 36 degrees, is this a number that can be expressed in terms of square roots?
The distance between two non-adjacent vertices of the pentagon with side 1 is the golden ratio, or (1+sqrt(5))/2. Given that, we can work out from the diagram that sin(18°) equals (sqrt(5)-1)/4.
That's because a horizontal line with length (1+sqrt(5))/2 in the diagram has one subtracted from it by taking verticals from the points at the bottom of the pentagon, and half that difference is sin(18°) as illustrated by the right triangle on the bottom right of the pentagon.
The distance from the vertices of the unit pentagon and its center can then be determined as half the golden ratio, (1+sqrt(5))/4, divided by the cosine of 18 degrees. And, of course, the sine of an angle, squared, plus the cosine of that same angle, squared, add to one.
So we have that this distance equals:
___
/
1 + / 5
\/
------------------------------------------------
______________________________
/
/ / ___ \ 2
/ | / |
/ | / 5 - 1 |
4 * / 1 - | \/ |
/ | --------------- |
/ | 4 |
/ \ /
\/
Copyright (c) 2001, 2002, 2006, 2007 John J. G. Savard