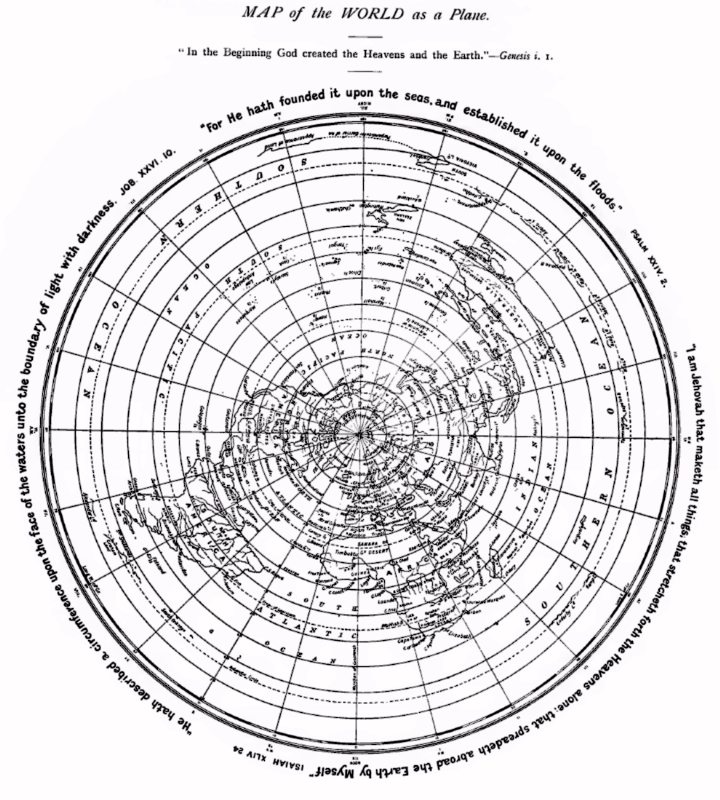
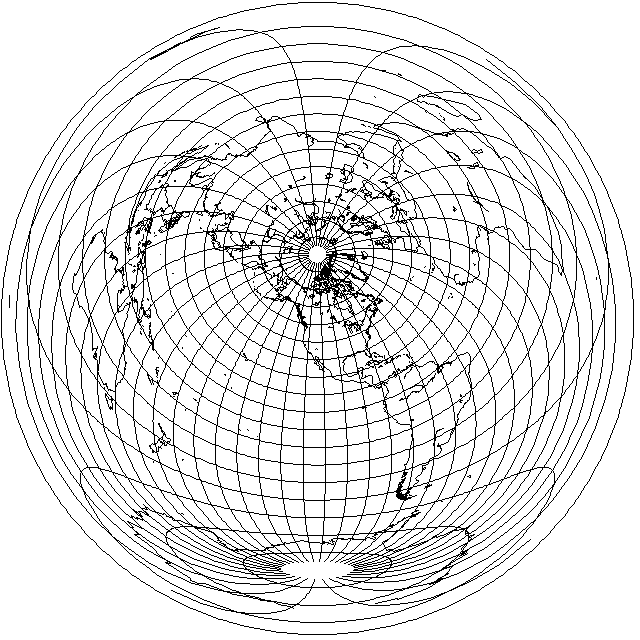
Here is a map of the world, drawn on the Azumuthal Equidistant projection, and centered on the North Pole.
There is one unusual thing about it: it is taken from a book, published in the year 1901, that argued that the Earth was flat, and that this map showed the actual shape of the Earth's surface.
If you never travel more than a hundred miles or so in any direction, there is no reason for the Earth not to seem flat to you, as far as you would know from direct experience. So this makes the idea that the Earth really is flat in its entirety a tempting one.
But in our age of jet travel, where the fact that one can go East by going West, as proven by the journey of Ferdinand Magellan, is a fact of everyday experience, one has to take the world as a whole into account.
Considering the world to have the shape shown by the map above is certainly a good try.
Have the Sun circle the North Pole, in a circle that shrinks during summer in the Northern Hemisphere and expands during the winter, at a suitable distance above the Earth, and one can account for world time zones, people going East from Vancouver, and West from New Delhi, and both ending up in Tokyo.
None the less, while this map represents a nice try, some things just don't add up.
Because Australia is at quite a southern latitude, it appears quite stretched on this map.
It would be easy enough for one person to set up a sundial in his garden in Sydney, on the East coast of Australia, and another person to set up a sundial in his backyard in Perth, on the West coast of Australia, to demonstrate that the observed solar time in those two cities does in fact differ by over two hours, as would be expected by them being separated by just over 35 degrees of longitude.
Since Sydney and Perth are both situated on the landmass of Australia, it is at least theoretically possible to journey from one of them to the other by automobile, and inspect one's odometer at the beginning and end of the journey.
This would not, in fact, be trivial. The area in the middle of Australia separating the two cities happens to be a fierce and inhospitable desert, not to be travelled lightly.
However, it is not as if a journey from Rockhampton to Camarvon, in more or less a straight line, by way of Alice Springs, is what is being discussed here. That, indeed, would be something best left to a convoy of experts, in a fleet of all-terrain vehicles well supplied with food and water.
Sydney and Perth are both in the south of Australia. So there are roads, for the most part close to the coastline, which significantly moderates the climate, so one could go from Sydney to Wagga Wagga and then Adelaide, and then proceed on from Adelaide to Port Augusta and then Kalgoorlie, and finally to Perth, and there would be at least actual roads on which to drive. There are even a number of other cities and towns along those roads, but it may still be necessary to take supplies of food, gasoline, and water as well as observing other safety precautions, for at least some stretches of the journey even so.
And the point of that, of course, is that if the distance from Sydney to Perth is not more than twice as long as a journey across 35 degrees of longitude in, say, Canada would be, then the circle upon the Earth made by the parallel of latitude for 30 degrees south latitude is too small to fit on a flat Earth of the type depicted, as instead the Earth closes up as one goes South, and the Earth must then be round... as this kind of flat Earth is the only alternative left.
The reason why I mention Australia, of course, is that one needs permission to travel to Antarctica, and one can't simply roam at will over its surface.
But there is another sphere, unlike the Earth, over which anyone can roam at will.
Here, I refer to the celestial sphere, that of the night sky.
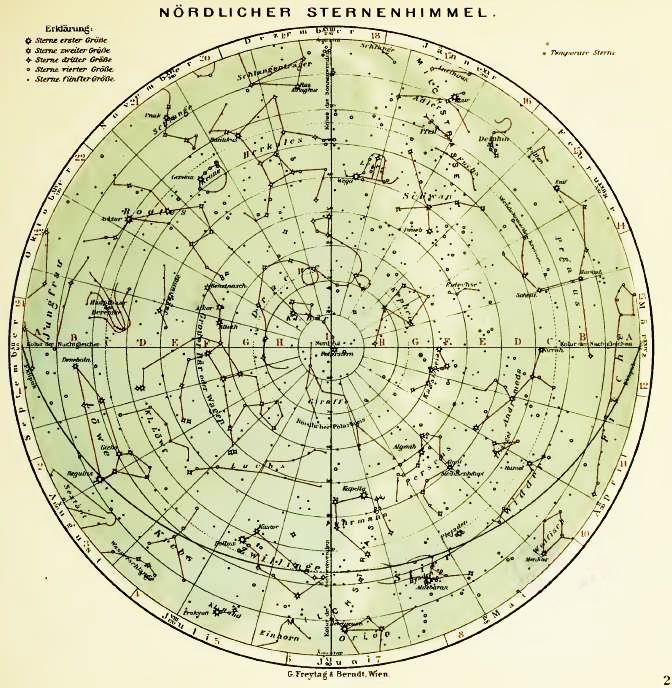
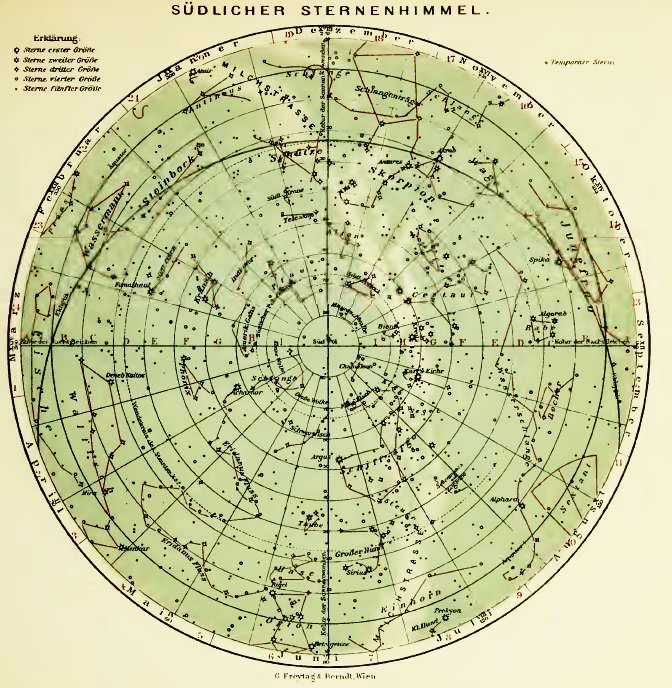
Here, from an old atlas, are maps of the northern and southern hemispheres of the starry sky.
Anyone can look up at the sky, and see almost a hemisphere's worth of the sky at night, so clearly these maps are not falsified or distorted - except for the stretching near the equator, because the projection doesn't correspond exactly to the globe.
Of course, we can deal with that by looking instead at the gores from an old celestial globe:
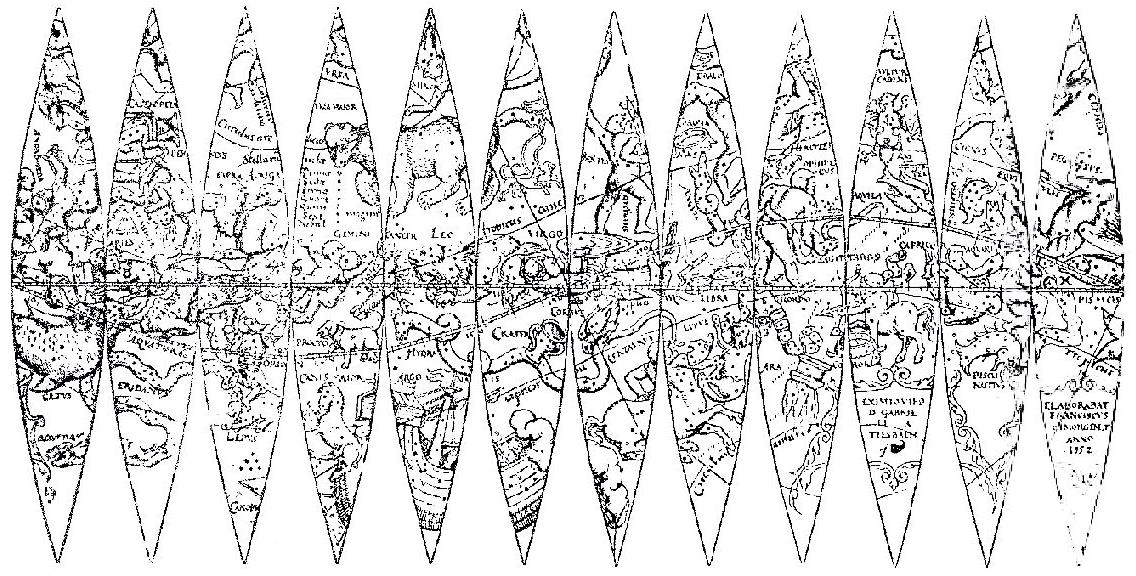
And wherever you live, during the course of a night, during the course of the seasons, you can see that the point directly above you in the sky, your zenith, describes a circle on this map of the night sky corresponding to your latitude.
This is, of course, why Ptolemy knew the Earth was round, even if he thought it too small because he did not know the proper distance from where he lived to a place at another latitude.
So all you have to do is look up at the stars to know that the Earth must be a globe, at least approximately, and can't possibly be flat.
I suppose that flat-Earth advocates could try other maps:
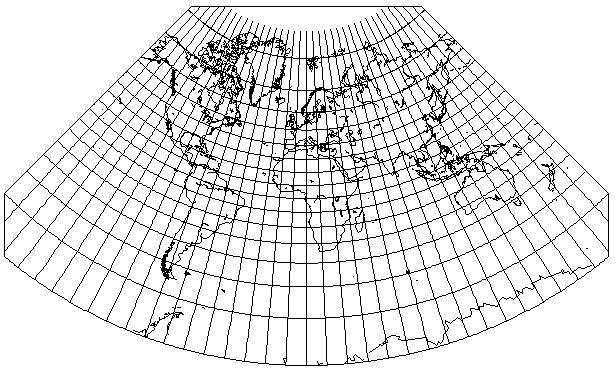
This is Herschel's projection, a particular case of Lambert's conformal conic projection.
The standard parallel is placed so that the "conic constant" is 1/4; that is, the world takes up one-quarter of a circle from the pole.
Because it's a conic projection with a limited angle, a degree of longitude at 30 degrees South latitude, where it would be in Australia, is about as much longer than a degree of longitude at 50 degrees North latitude, as in much of North America and Europe, as it would be on a globe.
So a flat Earth with four identical Suns circling above it, and ships and planes crossing the International Date Line actually sneaking around at high speed in order to uphold their part in the conspiracy... might almost be possible, which had this general shape, of course with the widths of lands at other latitudes being slightly adjusted.
Actually, using the program G.Projector to draw for me a Lambert Conformal Conic with standard parallels at 50° N and 30° S, I obtained this result:
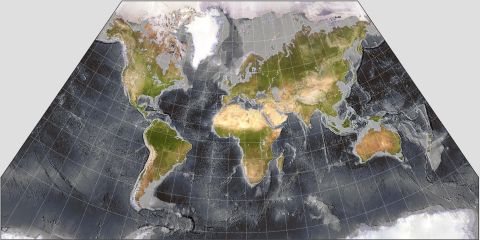
which suggests that there are five identical suns, with synchronized sunspots and so on, circling over our flat Earth... if one rejects what I still take to be the rather simpler hypothesis that it is spherical (but flattened slightly, by one part in 299 or so, and with other anomalies in the geoid of much smaller magnitude).
Also, if instead of using Lambert's Conformal Conic, one used the Simple Conic projection, which makes sense, as it keeps north-south distances the same, just as the Azimuthal Equidistant centered on the pole does, then one gets this result:
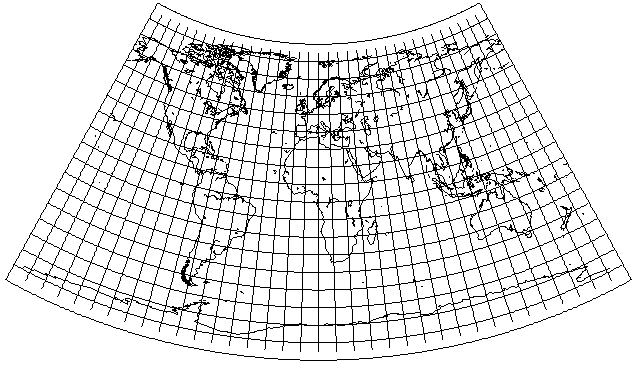
which now takes up about 1/6 th of a circle rather than 1/5 th, so it would require six identical suns to circle over it.