The short vector instructions operate on vectors of a fixed length, with a set of vector registers of that length available. These instructions resemble the MMX feature, or the later SSE (Streaming SIMD Extensions) and AVX (Advanced Vector eXtensions) features, of Intel microprocessors, or the AltiVec feature of both some Motorola 680x0 microprocessors and PowerPC microprocessors from Motorola, IBM, and others, or AMD's 3D Now! instructions, by operating on a relatively long word that can be split into multiple smaller segments.
The instructions dealt with on this page are available from both Normal Mode and Compressed Mode. The Short Vector Fourier Assist and Short Vector Type Conversion instructions are not available from Simple Mode; the others are available, but have different opcodes.
The Lincoln Laboratory TX-2 computer was a computer built from discrete transistors that could perform arithmetic on a 36-bit word or on its two halves or four quarters simultaneously; as well, the AN/FSQ-30 and 31 computers offered similar capabilities with their 48-bit word, and, earlier, the AN/FSQ-7 computer designed by IBM for SAGE operated on pairs of 16-bit numbers at a time, so there are some precedents for operations on vectors of small to medium size.
Also, both the VIS (Visual Instruction Set) instructions of the Sun SPARC and the MAX (Multimedia Acceleratin eXtensions) instructions of Hewlett-Packard's PA-RISC were available shortly before Intel introduced their MMX (Multi-Media eXtensions).
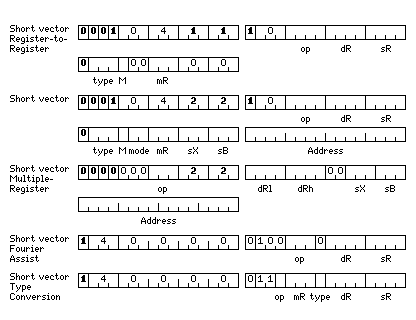
The short vector instructions have the formats:

and the opcodes of the standard short vector instructions are:
010422 1000xx 00xxxx SWBSV Swap Byte Short Vector 010422 1010xx 00xxxx LBSV Load Byte Short Vector 010422 1014xx 00xxxx STBSV Store Byte Short Vector 010422 1020xx 00xxxx ABSV Add Byte Short Vector 010422 1024xx 00xxxx SBSV Subtract Byte Short Vector 010422 1040xx 00xxxx SMBPB Set Mask Bit if Positive Byte 010422 1044xx 00xxxx SMBZB Set Mask Bit if Zero Byte 010422 1050xx 00xxxx SMBNB Set Mask Bit if Negative Byte 010422 1054xx 00xxxx XBSV XOR Byte Short Vector 010422 1060xx 00xxxx NBSV AND Byte Short Vector 010422 1064xx 00xxxx OBSV OR Byte Short Vector 010422 1000xx 01xxxx SWHSV Swap Halfword Short Vector 010422 1010xx 01xxxx LHSV Load Halfword Short Vector 010422 1014xx 01xxxx STHSV Store Halfword Short Vector 010422 1020xx 01xxxx AHSV Add Halfword Short Vector 010422 1024xx 01xxxx SHSV Subtract Halfword Short Vector 010422 1030xx 01xxxx MHSV Multiply Halfword Short Vector 010422 1034xx 01xxxx DHSV Divide Halfword Short Vector 010422 1040xx 01xxxx SMBPH Set Mask Bit if Positive Halfword 010422 1044xx 01xxxx SMBZH Set Mask Bit if Zero Halfword 010422 1050xx 01xxxx SMBNH Set Mask Bit if Negative Halfword 010422 1054xx 01xxxx XHSV XOR Halfword Short Vector 010422 1060xx 01xxxx NHSV AND Halfword Short Vector 010422 1064xx 01xxxx OHSV OR Halfword Short Vector 010422 1000xx 02xxxx SWSV Swap Short Vector 010422 1010xx 02xxxx LSV Load Short Vector 010422 1014xx 02xxxx STSV Store Short Vector 010422 1020xx 02xxxx ASV Add Short Vector 010422 1024xx 02xxxx SSV Subtract Short Vector 010422 1030xx 02xxxx MSV Multiply Short Vector 010422 1034xx 02xxxx DSV Divide Short Vector 010422 1040xx 02xxxx SMBP Set Mask Bit if Positive 010422 1044xx 02xxxx SMBZ Set Mask Bit if Zero 010422 1050xx 02xxxx SMBN Set Mask Bit if Negative 010422 1054xx 02xxxx XSV XOR Short Vector 010422 1060xx 02xxxx NSV AND Short Vector 010422 1064xx 02xxxx OSV OR Short Vector 010422 1000xx 03xxxx SWLSV Swap Long Short Vector 010422 1010xx 03xxxx LLSV Load Long Short Vector 010422 1014xx 03xxxx STLSV Store Long Short Vector 010422 1020xx 03xxxx ALSV Add Long Short Vector 010422 1024xx 03xxxx SLSV Subtract Long Short Vector 010422 1030xx 03xxxx MLSV Multiply Long Short Vector 010422 1034xx 03xxxx DLSV Divide Long Short Vector 010422 1040xx 03xxxx SMBPL Set Mask Bit if Positive Long 010422 1044xx 03xxxx SMBZL Set Mask Bit if Zero Long 010422 1050xx 03xxxx SMBNL Set Mask Bit if Negative Long 010422 1054xx 03xxxx XLSV XOR Long Short Vector 010422 1060xx 03xxxx NLSV AND Long Short Vector 010422 1064xx 03xxxx OLSV OR Long Short Vector 010422 1010xx 04xxxx LSMSV Load Small Short Vector 010422 1014xx 04xxxx STSMSV Store Small Short Vector 010422 1020xx 04xxxx ASMSV Add Small Short Vector 010422 1024xx 04xxxx SSMSV Subtract Small Short Vector 010422 1030xx 04xxxx MSMSV Multiply Small Short Vector 010422 1034xx 04xxxx DSMSV Divide Small Short Vector 010422 1040xx 04xxxx SMBPSM Set Mask Bit if Positive Small 010422 1044xx 04xxxx SMBZSM Set Mask Bit if Zero Small 010422 1050xx 04xxxx SMBNSM Set Mask Bit if Negative Small 010422 1010xx 05xxxx LFSV Load Floating Short Vector 010422 1014xx 05xxxx STFSV Store Floating Short Vector 010422 1020xx 05xxxx AFSV Add Floating Short Vector 010422 1024xx 05xxxx SFSV Subtract Floating Short Vector 010422 1030xx 05xxxx MFSV Multiply Floating Short Vector 010422 1034xx 05xxxx DFSV Divide Floating Short Vector 010422 1040xx 05xxxx SMBPF Set Mask Bit if Positive Floating 010422 1044xx 05xxxx SMBZF Set Mask Bit if Zero Floating 010422 1050xx 05xxxx SMBNF Set Mask Bit if Negative Floating 010422 1010xx 06xxxx LDSV Load Double Short Vector 010422 1014xx 06xxxx STDSV Store Double Short Vector 010422 1020xx 06xxxx ADSV Add Double Short Vector 010422 1024xx 06xxxx SDSV Subtract Double Short Vector 010422 1030xx 06xxxx MDSV Multiply Double Short Vector 010422 1034xx 06xxxx DDSV Divide Double Short Vector 010422 1040xx 06xxxx SMBPD Set Mask Bit if Positive Double 010422 1044xx 06xxxx SMBZD Set Mask Bit if Zero Double 010422 1050xx 06xxxx SMBND Set Mask Bit if Negative Double 010422 1000xx 07xxxx SWQSV Swap Quad Short Vector 010422 1010xx 07xxxx LQSV Load Quad Short Vector 010422 1014xx 07xxxx STQSV Store Quad Short Vector 010422 1020xx 07xxxx AQSV Add Quad Short Vector 010422 1024xx 07xxxx SQSV Subtract Quad Short Vector 010422 1030xx 07xxxx MQSV Multiply Quad Short Vector 010422 1034xx 07xxxx DQSV Divide Quad Short Vector 010422 1040xx 07xxxx SMBPQ Set Mask Bit if Positive Quad 010422 1044xx 07xxxx SMBZQ Set Mask Bit if Zero Quad 010422 1050xx 07xxxx SMBNQ Set Mask Bit if Negative Quad
In Simple Mode, these instructions will start with 044220 instead of 010422. This follows the general rule that instructions of the form:
00010abcdexyzxyz
in Normal Mode and Compact Mode are represented by instructions of the form
01abcdexyzxyz000
in Simple Mode, while instructions in Normal Mode and Compact Mode of the form
00011abcdexyzxyz
are not available from Simple Mode.
In addition, a set of instructions similar to the long format memory reference instructions and the long vector instructions is available that operates on short vectors:
These registers are 256 bits long, and are fully packed with data. Therefore, register-to-register floating-point operations of this type do not provide any guard bits which are retained between operations, unlike the normal floating-point registers, which retain floating-point numbers in an internal form, to be described later in the section on the basic aspects of this architecture which does include some additional bits of precision when values are of a type which does not fill the register.
This is not necessarily a bad thing, as it does lead to more consistent results. A limited number of guard bits, following normal ALU design practice, are used when carrying out the calculations themselves, and conversions similar to those made to internal floating-point formats would also be used during calculations to simplify ALU operation. Thus, the short vector ALU, in many cases, would be working with numbers in the same format as that given as the internal format used in the regular floating point registers, but four bits shorter; but the conversions to and from the external representation take place with every arithmetic operation. Similarly, the regular ALUs would also, when performing calculations, use four guard bits internally additional to those maintained in the regular floating-point registers. Therefore, the short vector ALUs would usually be eight bits less wide, not four bits less wide, than the regular ALUs for numbers of the same precision. Operating on quad precision floating-point numbers, which occupy 128 bits in the register in both cases, would usually be an exception to this, with the exception of the case of the compatible floating-point format, which does have eight additional in-register guard bits for its 128-bit floating-point formats, unlike the other 128-bit floating-point format, because it has an eight-bit redundant exponent field to eliminate internally.
These guard bits are not to be confused with the guard bit from the set of guard, round, and sticky bits used during the course of a single calculation to ensure an accurate result. While these are not available with the simple floating type, they are available for use with short vector operations.
This distinction may, perhaps, be clarified by means of the following table:
| Floating-point Type | Guard, Round, and Sticky Bits | Additional Guard Bits |
| Floating-Point Shorter than 128 bits in Regular Floating-Point Registers | Yes | Yes |
| 128-bit Floating-Point | Yes | No |
| Floating-Point in Short Vector Registers | Yes | No |
| Simple Floating Type | No | No |
If the bit marked M in the instruction is set, the bits of the accumulator/index register indicated by mR indicate which of the elements of the vector are operated on by the instruction. The short vector registers are each 256 bits in length; they can contain anything from two 128-bit quad precison floating-point numbers to thirty-two 8-bit bytes. For cases other than byte operations, the mask bits used are the contiguous least significant bits of the register selected.
The mode field in the instruction indicates the addressing mode. Its values are:
01 register-memory 10 memory-register
Thus, in mode 01, sR is not used; in mode 10, dR is not used, and sX and sB are used with a memory operand that is actually the destination rather than the source for the instruction.
Also, if the four-bit operate code is 1110, then:
The opcodes of the short vector multiple register instructions are:
Normal Simple Compact ------------- ------------- 000222 xxx0xx 102220 xxx0xx LSVM Load Short Vector Multiple 000322 xxx0xx 103220 xxx0xx STSVM Store Short Vector Multiple
These instructions allow a range of the short vector registers to be saved or loaded for purposes of context switching.
The opcodes of the short vector Fourier assist instructions are:
140000 044xxx SHSMHSV Shuffle Small/Halfword Short Vector 140000 045xxx SHFWSV Shuffle Floating/Word Short Vector 140000 046xxx SHDLSV Shuffle Double/Long Short Vector 140000 047xxx SHQSV Shuffle Quad Short Vector
These instructions are available only from Normal Mode and Compact Mode.
These instructions have a format similar to the short vector multiple-register instructions, but sX and sB are not used, and the fields shown as dRl and dRh for that format instead serve again as dR and sR respectively.
All these modes require that the source and destination be an even-numbered short-vector register, as they move data from the source register and the one following it to the destination register and the one following it.
The SHQSV instruction takes the four 128-bit quad-precision floating-point numbers in the source, and places them in the destination in the order:
0 2 1 3
The SHDLSV instruction divides the source into eight 64-bit blocks, and places them in the destination in the order:
0 4 1 5 2 6 3 7
The SHFWSV instruction divides the source into sixteen 32-bit blocks, and places them in the destination in the order:
0 8 1 9 2 10 3 11 4 12 5 13 6 14 7 15
The SHSMHSV instruction divides the source into thirty-two halfwords, and places them in the destination in the order:
0 16 1 17 2 18 3 19 4 20 5 21 6 22 7 23 8 24 9 25 10 26 11 27 12 28 13 29 14 30 15 31
These instructions are intended to assist in performing Fast-Fourier Transform operations using the short vector registers when either the long vector registers are not available to a process, or they do not exist, or are implemented in a slow fashion (i.e. simulated in main memory) on a particular implementation of the architecture.
Because Fast-Fourier Transform operations may be performed on different operand types, and because of the structure of the short vector registers, in the case of the short vector registers, as opposed to the long vector registers, instructions for assisting with the Stockham framework of the FFT rather than the Pease framework of the FFT were the ones provided with these registers.
This is more fully discussed on the next page, in which the FFT operations used for those modes, involving the Pease framework, as well as the other possible frameworks, are illustrated.
The type, in the first word of the instruction, can represent eight different types, seven of them being seven of the eight types used with conventional memory-reference instructions. The 48-bit Medium floating-point type is not allowed, as that length does not evenly subdivide a 256-bit vector. Instead, it is replaced by the Small type, which provides 16-bit floating-point numbers for use in applications such as signal analysis.
Three formats are available for floating-point numbers with this length. Two bits of the Program Status Block control the format of Small floating-point numbers; these are independent of the nine-bit field in the Program Status Block that controls the format of floating-point numbers of other sizes.
The first possible format is modelled after the Standard floating-point format. It is also a standard format in its own right, as it is used by advanced graphics chips that perform 3-D acceleration on personal computers.
In this format, numbers consist of a sign bit, five exponent bits in excess-14 format, and ten mantissa bits, not including the first bit of the mantissa, which is a hidden 1 bit. For an all-zero exponent field, there is no longer a hidden one bit, but numbers can be unnormalized to allow gradual underflow.
In this format, some possible numeric values are:
Data Item Numeric Value Power of Two 0 11110 1111111111 65,504 0 11110 0000000000 32,768 15 0 10000 0000000000 2 1 0 01111 1000000000 1.5 0 01111 0000000000 1 0 0 01110 0000000000 .5 -1 0 00001 0000000000 6.10352 * 10^(-4) -14 0 00000 1000000000 3.05176 * 10^(-4) -15 0 00000 0100000000 1.52588 * 10^(-4) -16 0 00000 0000000001 5.96046 * 10^(-8) -24 0 00000 0000000000 0
The maximum possible exponent value, 11111, is reserved for infinities and NaN values exactly as in the Standard floating-point format.
Numbers in the second of these formats have two exponent bits, and are encoded using extremely gradual underflow in a sophisticated manner which allows them to be compared using integer comparison instructions.
For a positive number, the fields in its representation are:
If the number is negative, 1 is used for the sign bits, and the remaining portion of the number still follows the same format, but all the bits in it are inverted (that is, a one's complement is performed).
The exponent is taken as being an unsigned number, and the binary point of the mantissa as being before its first digit; thus, some example values in this encoding are shown below:
16-bit Small Fields Numeric Power of
Data Item Value Two
0111111111111111 0 1 11 111111111111 7.99951
0111000000000000 0 1 11 000000000000 4 2
0110111111111111 0 1 10 111111111111 3.99976
0110000000000000 0 1 10 000000000000 2 1
0101000000000000 0 1 01 000000000000 1 0
0100000000000000 0 1 00 000000000000 .5 -1
0011100000000000 0 01 11 00000000000 .25 -2
0011000000000000 0 01 10 00000000000 .125 -3
0010100000000000 0 01 01 00000000000 .0625 -4
0010000000000000 0 01 00 00000000000 .03125 -5
0001110000000000 0 001 11 0000000000 .015625 -6
0000111000000000 0 0001 11 000000000 9.76562 * 10^(-3) -10
0000011100000000 0 00001 11 00000000 6.10352 * 10^(-4) -14
0000001110000000 0 000001 11 0000000 3.81470 * 10^(-5) -18
0000000111000000 0 0000001 11 000000 2.38419 * 10^(-6) -22
0000000011100000 0 00000001 11 00000 1.49012 * 10^(-7) -26
0000000001110000 0 000000001 11 0000 9.31323 * 10^(-9) -30
0000000000111000 0 0000000001 11 000 5.82077 * 10^(-10) -34
0000000000011100 0 00000000001 11 00 3.63798 * 10^(-11) -38
0000000000001110 0 000000000001 11 0 2.27374 * 10^(-12) -42
0000000000000111 0 0000000000001 11 1.42109 * 10^(-13) -46
0000000000000110 0 0000000000001 10 7.10543 * 10^(-14) -47
0000000000000101 0 0000000000001 01 3.55271 * 10^(-14) -48
0000000000000100 0 0000000000001 00 1.77636 * 10^(-14) -49
0000000000000011 0 00000000000001 1 8.88178 * 10^(-15) -50
0000000000000010 0 00000000000001 0 4.44089 * 10^(-15) -51
0000000000000001 0 000000000000001 2.22045 * 10^(-15) -52
0000000000000000 0 000000000000000 0
Note that at the low end of the range, the exponent field shrinks from two bits to one and then zero bits. This produces a distribution of represented points similar to that provided by A-law audio encoding.
As early music-quality digital audio systems used 14-bit fixed-point samples instead of 16-bit ones, I envisaged this format as an alternative to fixed-point samples for uncompressed digital audio applications. However, there is a problem with using floating-point samples; since soft sounds are not always masked by loud sounds in different frequency ranges, the shifting noise floor of floating-point encoding can be distracting. One remedy would be to apply floating-point encoding to a transformed signal that has already been divided into critical bands: these are the narrow frequency ranges within which sounds do mask each other, and they are used as part of the compression algorithms for the Digital Compact Cassette (DCC) from Philips and the MiniDisc from Sony. It would also be appropriate to apply equalization, because low-frequency components of music will typically have much larger amplitudes than high-frequency components; the less rapid motion in low-frequency vibrations means that they have much less energy for a given amplitude than high-frequency vibrations.
The third possible format for 16-bit floating-point numbers attempts to provide a very wide exponent range. Numbers normally consist of a sign bit, three exponent bits in excess-4 format, and twelve mantissa bits, which do not include a hidden 1 bit. This is true when the exponent begins with 01 or 10. The size of the exponent is increased by two bits for every additional 0 or 1 that follows the initial 0 or 1 respectively, until the size of the mantissa field is reduced to a minimum of eight bits in length. The lowest possible value for the exponent field is thus an all-zeroes exponent field, which will be seven bits long; this will recieve the same special treatment as it does in the Standard floating-point format, moving the radix point one place and not having a hidden first one bit, to allow zero to be represented; thus, only gradual underflow takes place for the most extreme small values, which are also the only values to have a precision of less than nine bits.
Some representative values in this format are:
0 1111111 11111111 2,093,056 0 1111111 00000000 1,048,576 20 0 1110111 00000000 4,096 12 0 1110000 00000000 32 5 0 11011 0000000000 16 4 0 11000 0000000000 2 1 0 101 110000000000 1.75 0 101 100000000000 1.5 0 101 010000000000 1.25 0 101 000000000000 1 0 0 100 000000000000 .5 -1 0 011 000000000000 .25 -2 0 010 000000000000 .125 -3 0 00111 0000000000 .0625 -4 0 00100 0000000000 .0078125 -7 0 0001111 00000000 .00390625 -8 0 0001000 00000000 3.05176 * 10^(-5) -15 0 0000001 00000000 2.38419 * 10^(-7) -22 0 0000000 10000000 1.19209 * 10^(-7) -23 0 0000000 01000000 5.96046 * 10^(-8) -24 0 0000000 00000001 2.98023 * 10^(-8) -30 0 0000000 00000000 0
Extra instructions are defined to permit conversion between this particular number type, not used anywhere else, and more conventional types:
140000 06x0xx CFSMSV Convert Floating to Small Short Vector 140000 07x0xx CSMFSV Convert Small to Floating Short Vector
Here, to permit use of the mask bit and a mask register with the instructions, where the type bits are 2 or 3, the three-bit opcode field is moved from the mR field to the dR field.
The destination operand is always a single short vector register considered as being divided into sixteen quantities of type small; the source operand is either a pair of short vector registers containing sixteen quantities of type floating or four short vector registers containing sixteen quantities of type long.
A pair of short vector registers must begin with an even-numbered one; a group of four must begin with short vector register 0, 4, 8 or 12.