Most of the computer's instructions tell it to perform a particular basic arithmetic calculation. The form of these instructions is shown below:
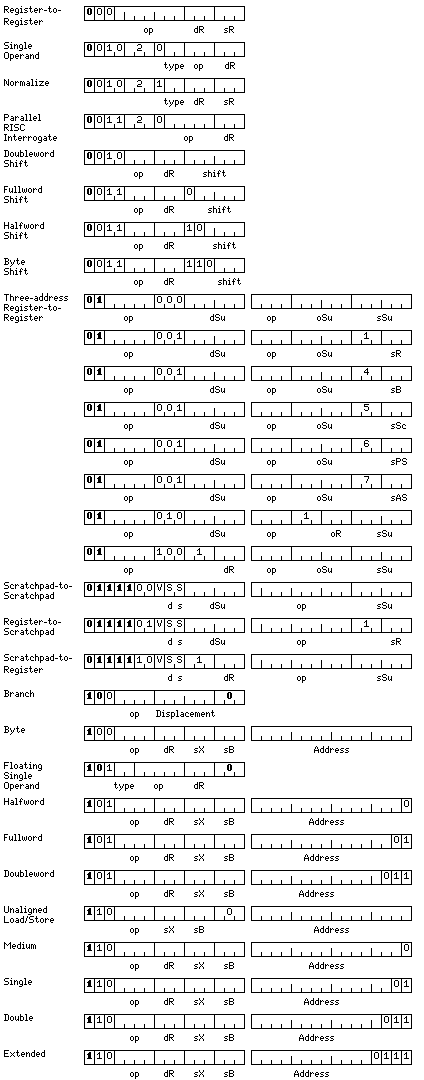
In addition to the register to register instructions, and the memory-reference instructions, the diagram also illustrates certain other instructions, the decoding of which is intertwined with that of these instructions.
Because this diagram shows the instructions which make up the largest proportion of the opcode space of the system, this is an appropriate point at which to note that instructions have been designed so as to simplify determining the length of an instruction.
While the scheme is not as simple as that of the IBM 360, in which, originally, an instruction began with 00 if it was 16 bits long, 01 or 10 if it was 32 bits long, and 11 if it was 48 bits long, it still allows the length of an instruction to be determined without fully completing the decoding of an instruction.
As can be seem from the diagram above, usually
0xxxxxxxxxxxxxxx: 16-bit instruction 1xxxxxxxxxxxxxxx: 32-bit instruction
but with the exception that if an instruction begins with 10, and the last three bits, indicating the base register, are zero, then additional 16-bit instructions are indicated.
Also, instructions of the form
00101mmvssxxxxxx
are two-address instructions where the length of the instruction is specified in two parts separately, as a consequence of the addressing modes of the source and destination operands, which may be independently indicated as requiring address fields. Three of the simplest addressing modes for instructions of this type are shown in the diagram; this type of instruction will be discussed in a later section.
As well, instructions of the form
010xxxxxxxxxxxxx
include three-address instructions which allow use of any of the sixty-four supplementary registers, as well as registers from several sets of eight registers. Allowing this type of operation to be specified in only 32 bits is a capability usually provided by RISC architectures.
This group of instructions also includes indexed instructions which offer post-indexed indirect addressing. The scratchpad registers point to regions containing 4,096 addresses, which can be pointers to arrays, so that one scratchpad register can be used to facilitate reference to that many arrays regardless of their size. With conventional memory-reference instructions, each base register points to a region 65,536 bytes in size, and any arrays accessed by means of indexed addressing need to fit in that region, with the possible exception of one array that begins in the area accessible by possible displacements, but extends beyond the block. Thus, if a large number (more than seven) of large arrays (more than 65,536 bytes in size) are in use by any one program, without this mode it becomes necessary to reload one or more base registers when accessing different arrays.
A further exception is not visible on this diagram. Longer instructions are indicated by their first 16 bits corresponding to a register-to-register instruction where the destination register and source register fields are identical.
In a register-to-register instruction, the source and destination registers must be different. When these two fields contain the same number, the instruction is instead decoded to provide an instruction with an advanced addressing mode, for such things as string, packed decimal, or vector operations, or to provide an instruction other than a memory-reference instruction, such as an operate instruction.
Thus, in order for an instruction to be greater than 32 bits in length, the form of the first 16 bits must be the following:
000pxxxxxxabcabc
If the bit marked p is 1, the instruction is followed by a series of additional 16-bit units of which all but the last start with 1, and the last of which starts with 0. (There may be only one such 16-bit unit, starting with zero.) If it is zero, this section of the instruction is not present.
The bits marked abc both contain the number of 16-bit units without any restriction as to their first bit which appear at the end of the instruction. If the p bit is a one, the section of the instruction it indicates precedes these halfwords.
Generally, the section of the instruction indicated by the p bit consists of halfwords which contain various fields relating to the operation to be performed, while the section indicated by the two copies of abc will chiefly consist of halfwords containing addresses.
When the p bit is a one, it is possible for the abc fields to both contain zero, for this format, since that may still result in an instruction longer than 32 bits.
When the p bit is a zero, and the two abc fields both contain 001, as this format would normally indicate an instruction 32 bits in length by the scheme above, and would therefore be redundant, it indicates instead that the instruction will be a three-address instruction with fields which indicate separately if address values are appended to the instruction for the source, operand, and destination operands of the instruction. The PDP-11 is a well-known example of an architecture with this type of instruction; here, the address modes are more complicated, as this instruction format is used for vector arithmetic.
These instructions indicate the addressing modes used in the same way as the two-address instructions beginning with 00111xxxxxxxxxxx except with some of the relevant bits being in different positions.
A two-address instruction has only source and destination operands; in the case of a subtract instruction, the contents of the source operand are subtracted from the contents of the destination operand, and the result is placed in the destination operand. In a three-address subtract instruction, the contents of the source operand are subtracted from the contents of the operand operand, and the result is placed in the destination operand.
When the p bit is a zero, and the two abc fields both contain 000, this arrangement is also redundant, as it would indicate an instruction 16 bits in length. Therefore, this format instead indicates the 16-bit halfword is a 16-bit prefix which precedes an instruction the length of which is determined normally. This allows the potential of future expansion of the opcode space.
Additionally, 32-bit prefixes are also possible; what would be a 32-bit instruction of the form:
1100001xxxxxx000 xxxxxxxxxxxxxxxx
is instead a 32-bit prefix for an instruction, again, one the length of which is decoded normally.
One ingenious idea that allows some opcode space to be obtained from nearly any instruction format without any compromise was used in the SEL 32 series of computers, by Systems Engineering Laboratories. This firm made minicomputers, and it was located in Fort Lauderdale, Florida and NASA was one of its main customers.
Instructions were made more compact by only allowing aligned operands to be addressed. The unused least significant bits of the address in most cases were used to help indicate operand type in the instruction. (This idea is used not only in the regular memory-reference instructions, but in the 16-bit short format memory-reference instructions, and a similar principle is used to halve the amount of opcode space taken up by the shift instructions.)
The dR and sR fields, giving the destination register and the source register for an operation, can contain any value from 0 to 7.
The sB field, indicating the base/address register whose contents indicate the general area in memory from which a memory operand comes, can only contain a value from 1 to 7. When the sB field is zero in what would have been a memory-reference instruction with single-byte operands, this indicates the instruction only occupies a single 16-bit unit in memory, and is a branch instruction. When the sB field is zero in what would have been a memory-reference instruction with other fixed-point operands, this also indicates the instruction only occupies a single 16-bit unit in memory, but in this case it is a floating-point single-operand instruction. When the sB field is zero for what would have been a floating-point memory-reference instruction, the instruction still occupies two 16-bit units in memory, and is an instruction which performs either a load and store, for any of the basic fixed-point or floating-point types, from the appropriate register zero, to any memory address without alignment restrictions.
Also, and more simply, in a memory-reference instruction, the sX field, which indicates the arithmetic/index register whose contents are used to select the element of an array used as a memory operand, can only cause arithmetic/index registers 1 through 7 to act as the index register for the instruction. If this field contains zero, this indicates that indexing does not take place.
Also, a set of three-address register-to-register instructions is provided that are 32 bits in length, and which allow access to the base registers and the various types of scratchpad registers as well as the arithmetic-index registers, the floating-point registers, and the supplementary registers.
Thus, although there are instructions of different lengths, and many of the longer instructions still do not follow the load/store model, in this mode the processor has a full load/store instruction set similar to that of a RISC design, in addition to other non-RISC instructions.
These instructions have nine bits allocated to the opcode, divided between the first two halfwords of the instruction, but the first three bits of the opcode cannot both be 1. This allows these instructions to include additional opcodes for the instructions for the simple floating, decimal exponent, register packed, and floating register compressed types, which will be discussed later.
In addition, since the fixed-point instructions of this group normally have the 64-bit supplementary registers as their destinations, a set of 32-bit integer instructions which use the high 32 bits of their destination register is provided. This is inspired by a similar feature recently added by IBM to its z/Architecture systems with the zEnterprise z196. It differs in that instructions working with the 8-bit or 16-bit types are not included, on the one hand, and, on the other, that multiplication and division instructions are added (but not the multiply extensibly and divide extensibly instructions, which are more closely analogous to the multiply and divide instructions on the IBM 360 architecture).
Note that while most store instructions are omitted as not applicable to the three-address register-to-register instructions, the store high instructions are retained, since they move the high word of the destination operand to the low word of the source operand, while the load high instructions move the low word of the source operand to the high word of the destination operand, and thus both instructions perform distinct and necessary operations.
Note that normal memory-reference instructions will be incompatible with Subdivided Double operation in those cases where it causes double-precision operands to be reduced in size, since (as an example) address values are only available for all positions in memory containing an aligned 64-bit double-precision value, four of which are contained in a 256-bit memory word, and so address values will not be available for all the aligned 51-bit double-precision values which may be used in that mode. Register to register instructions, and unaligned load/store instructions, as well as scratchpad to register instructions, can still be used. |
The opcodes for memory-reference, register-to-register, and three-address register instructions are:
Memory Reference Register Three-Address
-------------------- ------ ------
100xxx xxxxxx 0000xx 040xxx 00xxxx SWB Swap Byte
101xxx xxxxxx 0002xx 040xxx 01xxxx CB Compare Byte
102xxx xxxxxx 0004xx 040xxx 02xxxx LB Load Byte
103xxx xxxxxx STB Store Byte
104xxx xxxxxx 0010xx 040xxx 04xxxx AB Add Byte
105xxx xxxxxx 0012xx 040xxx 05xxxx SB Subtract Byte
110xxx xxxxxx 0020xx 040xxx 10xxxx IB Insert Byte
111xxx xxxxxx 0022xx 040xxx 11xxxx UCB Unsigned Compare Byte
112xxx xxxxxx 0024xx 040xxx 12xxxx ULB Unsigned Load Byte
113xxx xxxxxx 0026xx 040xxx 13xxxx XB XOR Byte
114xxx xxxxxx 0030xx 040xxx 14xxxx NB AND Byte
115xxx xxxxxx 0032xx 040xxx 15xxxx OB OR Byte
117xxx xxxxxx 0036xx STGB Store if Greater Byte
120xxx xxxxx0 (xxx0) 0040xx 041xxx 00xxxx SWH Swap Halfword
121xxx xxxxx0 (xxx0) 0042xx 041xxx 01xxxx CH Compare Halfword
122xxx xxxxx0 (xxx0) 0044xx 041xxx 02xxxx LH Load Halfword
123xxx xxxxx0 (xxx0) STH Store Halfword
124xxx xxxxx0 (xxx0) 0050xx 041xxx 04xxxx AH Add Halfword
125xxx xxxxx0 (xxx0) 0052xx 041xxx 05xxxx SH Subtract Halfword
126xxx xxxxx0 (xxx0) 0054xx 041xxx 06xxxx MH Multiply Halfword
127xxx xxxxx0 (xxx0) 0056xx 041xxx 07xxxx DH Divide Halfword
130xxx xxxxx0 (xxx0) 0060xx 041xxx 10xxxx IH Insert Halfword
131xxx xxxxx0 (xxx0) 0062xx 041xxx 11xxxx UCH Unsigned Compare Halfword
132xxx xxxxx0 (xxx0) 0064xx 041xxx 12xxxx ULH Unsigned Load Halfword
133xxx xxxxx0 (xxx0) 0066xx 041xxx 13xxxx XH XOR Halfword
134xxx xxxxx0 (xxx0) 0070xx 041xxx 14xxxx NH AND Halfword
135xxx xxxxx0 (xxx0) 0072xx 041xxx 15xxxx OH OR Halfword
136xxx xxxxx0 (xxx0) 0074xx 041xxx 16xxxx MEH Multiply Extensibly Halfword
137xxx xxxxx0 (xxx0) 0076xx 041xxx 17xxxx DEH Divide Extensibly Halfword
120xxx xxxxx1 (xx01) 0100xx 042xxx 00xxxx SW Swap
121xxx xxxxx1 (xx01) 0102xx 042xxx 01xxxx C Compare
122xxx xxxxx1 (xx01) 0104xx 042xxx 02xxxx L Load
123xxx xxxxx1 (xx01) ST Store
124xxx xxxxx1 (xx01) 0110xx 042xxx 04xxxx A Add
125xxx xxxxx1 (xx01) 0112xx 042xxx 05xxxx S Subtract
126xxx xxxxx1 (xx01) 0114xx 042xxx 06xxxx M Multiply
127xxx xxxxx1 (xx01) 0116xx 042xxx 07xxxx D Divide
131xxx xxxxx1 (xx01) 0122xx 042xxx 11xxxx UC Unsigned Compare
133xxx xxxxx1 (xx01) 0126xx 042xxx 13xxxx X XOR
134xxx xxxxx1 (xx01) 0130xx 042xxx 14xxxx N AND
135xxx xxxxx1 (xx01) 0132xx 042xxx 15xxxx O OR
136xxx xxxxx1 (xx01) 0134xx 042xxx 16xxxx ME Multiply Extensibly
137xxx xxxxx1 (xx01) 0136xx 042xxx 17xxxx DE Divide Extensibly
120xxx xxxxx3 (x011) 0140xx 043xxx 00xxxx SWL Swap Long
121xxx xxxxx3 (x011) 0142xx 043xxx 01xxxx CL Compare Long
122xxx xxxxx3 (x011) 0144xx 043xxx 02xxxx LL Load Long
123xxx xxxxx3 (x011) STL Store Long
124xxx xxxxx3 (x011) 0150xx 043xxx 04xxxx AL Add Long
125xxx xxxxx3 (x011) 0152xx 043xxx 05xxxx SL Subtract Long
126xxx xxxxx3 (x011) 0154xx 043xxx 06xxxx ML Multiply Long
127xxx xxxxx3 (x011) 0156xx 043xxx 07xxxx DL Divide Long
131xxx xxxxx3 (x011) 0162xx 043xxx 11xxxx UCL Unsigned Compare Long
133xxx xxxxx3 (x011) 0166xx 043xxx 13xxxx XL XOR Long
134xxx xxxxx3 (x011) 0170xx 043xxx 14xxxx NL AND Long
135xxx xxxxx3 (x011) 0172xx 043xxx 15xxxx OL OR Long
136xxx xxxxx3 (x011) 0174xx 043xxx 16xxxx MEL Multiply Extensibly Long
137xxx xxxxx3 (x011) 0176xx 043xxx 17xxxx DEL Divide Extensibly Long
140xxx xxxxx0 (xxx0) 0200xx 044xxx 00xxxx SWM Swap Medium
141xxx xxxxx0 (xxx0) 0202xx 044xxx 01xxxx CM Compare Medium
142xxx xxxxx0 (xxx0) 0204xx 044xxx 02xxxx LM Load Medium
143xxx xxxxx0 (xxx0) STM Store Medium
144xxx xxxxx0 (xxx0) 0210xx 044xxx 04xxxx AM Add Medium
145xxx xxxxx0 (xxx0) 0212xx 044xxx 05xxxx SM Subtract Medium
146xxx xxxxx0 (xxx0) 0214xx 044xxx 06xxxx MM Multiply Medium
147xxx xxxxx0 (xxx0) 0216xx 044xxx 07xxxx DM Divide Medium
150xxx xxxxx0 (xxx0) 044xxx 10xxxx MEUM Multiply Extensibly Unnormalized Medium
151xxx xxxxx0 (xxx0) 044xxx 11xxxx DEUM Divide Extensibly Unnormalized Medium
152xxx xxxxx0 (xxx0) 044xxx 12xxxx LUM Load Unnormalized Medium
153xxx xxxxx0 (xxx0) 044xxx 13xxxx STUM Store Unnormalized Medium
154xxx xxxxx0 (xxx0) 044xxx 14xxxx AUM Add Unnormalized Medium
155xxx xxxxx0 (xxx0) 044xxx 15xxxx SUM Subtract Unnormalized Medium
156xxx xxxxx0 (xxx0) 044xxx 16xxxx MUM Multiply Unnormalized Medium
157xxx xxxxx0 (xxx0) 044xxx 17xxxx DUM Divide Unnormalized Medium
140xxx xxxxx1 (xx01) 0220xx 045xxx 00xxxx SWF Swap Floating
141xxx xxxxx1 (xx01) 0222xx 045xxx 01xxxx CF Compare Floating
142xxx xxxxx1 (xx01) 0224xx 045xxx 02xxxx LF Load Floating
143xxx xxxxx1 (xx01) STF Store Floating
144xxx xxxxx1 (xx01) 0230xx 045xxx 04xxxx AF Add Floating
145xxx xxxxx1 (xx01) 0232xx 045xxx 05xxxx SF Subtract Floating
146xxx xxxxx1 (xx01) 0234xx 045xxx 06xxxx MF Multiply Floating
147xxx xxxxx1 (xx01) 0236xx 045xxx 07xxxx DF Divide Floating
150xxx xxxxx1 (xx01) 045xxx 10xxxx MEU Multiply Extensibly Unnormalized
151xxx xxxxx1 (xx01) 045xxx 11xxxx DEU Divide Extensibly Unnormalized
152xxx xxxxx1 (xx01) 045xxx 12xxxx LU Load Unnormalized
153xxx xxxxx1 (xx01) STU Store Unnormalized
154xxx xxxxx1 (xx01) 045xxx 14xxxx AU Add Unnormalized
155xxx xxxxx1 (xx01) 045xxx 15xxxx SU Subtract Unnormalized
156xxx xxxxx1 (xx01) 045xxx 16xxxx MU Multiply Unnormalized
157xxx xxxxx1 (xx01) 045xxx 17xxxx DU Divide Unnormalized
140xxx xxxxx3 (x011) 0240xx 046xxx 00xxxx SWD Swap Double
141xxx xxxxx3 (x011) 0242xx 046xxx 01xxxx CD Compare Double
142xxx xxxxx3 (x011) 0244xx 046xxx 02xxxx LD Load Double
143xxx xxxxx3 (x011) STD Store Double
144xxx xxxxx3 (x011) 0250xx 046xxx 04xxxx AD Add Double
145xxx xxxxx3 (x011) 0252xx 046xxx 05xxxx SD Subtract Double
146xxx xxxxx3 (x011) 0254xx 046xxx 06xxxx MD Multiply Double
147xxx xxxxx3 (x011) 0256xx 046xxx 07xxxx DD Divide Double
150xxx xxxxx3 (x011) 046xxx 10xxxx MEUD Multiply Extensibly Unnormalized Double
151xxx xxxxx3 (x011) 046xxx 11xxxx DEUD Divide Extensibly Unnormalized Double
152xxx xxxxx3 (x011) 046xxx 12xxxx LUD Load Unnormalized Double
153xxx xxxxx3 (x011) STUD Store Unnormalized Double
154xxx xxxxx3 (x011) 046xxx 14xxxx AUD Add Unnormalized Double
155xxx xxxxx3 (x011) 046xxx 15xxxx SUD Subtract Unnormalized Double
156xxx xxxxx3 (x011) 046xxx 16xxxx MUD Multiply Unnormalized Double
157xxx xxxxx3 (x011) 046xxx 17xxxx DUD Divide Unnormalized Double
140xxx xxxxx7 (0111) 0260xx 047xxx 00xxxx SWQ Swap Quad
141xxx xxxxx7 (0111) 0262xx 047xxx 01xxxx CQ Compare Quad
142xxx xxxxx7 (0111) 0264xx 047xxx 02xxxx LQ Load Quad
143xxx xxxxx7 (0111) STQ Store Quad
144xxx xxxxx7 (0111) 0270xx 047xxx 04xxxx AQ Add Quad
145xxx xxxxx7 (0111) 0272xx 047xxx 05xxxx SQ Subtract Quad
146xxx xxxxx7 (0111) 0274xx 047xxx 06xxxx MQ Multiply Quad
147xxx xxxxx7 (0111) 0276xx 047xxx 07xxxx DQ Divide Quad
150xxx xxxxx7 (0111) 047xxx 10xxxx MEUQ Multiply Extensibly Unnormalized Quad
151xxx xxxxx7 (0111) 047xxx 11xxxx DEUQ Divide Extensibly Unnormalized Quad
152xxx xxxxx7 (0111) 047xxx 12xxxx LUQ Load Unnormalized Quad
153xxx xxxxx7 (0111) STUQ Store Unnormalized Quad
154xxx xxxxx7 (0111) 047xxx 14xxxx AUQ Add Unnormalized Quad
155xxx xxxxx7 (0111) 047xxx 15xxxx SUQ Subtract Unnormalized Quad
156xxx xxxxx7 (0111) 047xxx 16xxxx MUQ Multiply Unnormalized Quad
157xxx xxxxx7 (0111) 047xxx 17xxxx DUQ Divide Unnormalized Quad
050xxx 00xxxx SWHG Swap High
050xxx 01xxxx CHG Compare High
050xxx 02xxxx LHG Load High
050xxx 03xxxx STHG Store High
050xxx 04xxxx AHG Add High
050xxx 05xxxx SHG Subtract High
050xxx 06xxxx MHG Multiply High
050xxx 07xxxx DHG Divide High
050xxx 11xxxx UCHG Unsigned Compare High
050xxx 13xxxx XHG XOR High
050xxx 14xxxx NHG AND High
050xxx 15xxxx OHG OR High
051xxx 00xxxx SFSWL Simple Floating Swap Halfword
051xxx 01xxxx SFCL Simple Floating Compare Halfword
051xxx 02xxxx SFLL Simple Floating Load Halfword
051xxx 04xxxx SFAL Simple Floating Add Halfword
051xxx 05xxxx SFSL Simple Floating Subtract Halfword
051xxx 06xxxx SFML Simple Floating Multiply Halfword
051xxx 07xxxx SFDL Simple Floating Divide Halfword
051xxx 10xxxx SFMEUH Simple Floating Multiply Extensibly Unnormalized Halfword
051xxx 11xxxx SFDEUH Simple Floating Divide Extensibly Unnormalized Halfword
051xxx 12xxxx SFLUH Simple Floating Load Unnormalized Halfword
051xxx 14xxxx SFAUH Simple Floating Add Unnormalized Halfword
051xxx 15xxxx SFSUH Simple Floating Subtract Unnormalized Halfword
051xxx 16xxxx SFMUH Simple Floating Multiply Unnormalized Halfword
051xxx 17xxxx SFDUH Simple Floating Divide Unnormalized Halfword
052xxx 00xxxx SFSW Simple Floating Swap
052xxx 01xxxx SFC Simple Floating Compare
052xxx 02xxxx SFL Simple Floating Load
052xxx 04xxxx SFA Simple Floating Add
052xxx 05xxxx SFS Simple Floating Subtract
052xxx 06xxxx SFM Simple Floating Multiply
052xxx 07xxxx SFD Simple Floating Divide
052xxx 00xxxx SFMEU Simple Floating Multiply Extensibly Unnormalized
052xxx 01xxxx SFDEU Simple Floating Divide Extensibly Unnormalized
052xxx 02xxxx SFLU Simple Floating Load Unnormalized
052xxx 04xxxx SFAU Simple Floating Add Unnormalized
052xxx 05xxxx SFSU Simple Floating Subtract Unnormalized
052xxx 06xxxx SFMU Simple Floating Multiply Unnormalized
052xxx 07xxxx SFDU Simple Floating Divide Unnormalized
053xxx 00xxxx SFSWL Simple Floating Swap Long
053xxx 01xxxx SFCL Simple Floating Compare Long
053xxx 02xxxx SFLL Simple Floating Load Long
053xxx 04xxxx SFAL Simple Floating Add Long
053xxx 05xxxx SFSL Simple Floating Subtract Long
053xxx 06xxxx SFML Simple Floating Multiply Long
053xxx 07xxxx SFDL Simple Floating Divide Long
053xxx 10xxxx SFMEUL Simple Floating Multiply Extensibly Unnormalized Long
053xxx 11xxxx SFDEUL Simple Floating Divide Extensibly Unnormalized Long
053xxx 12xxxx SFLUL Simple Floating Load Unnormalized Long
053xxx 14xxxx SFAUL Simple Floating Add Unnormalized Long
053xxx 15xxxx SFSUL Simple Floating Subtract Unnormalized Long
053xxx 16xxxx SFMUL Simple Floating Multiply Unnormalized Long
053xxx 17xxxx SFDUL Simple Floating Divide Unnormalized Long
054xxx 01xxxx RPC Register Packed Compare
054xxx 02xxxx RPME Register Packed Multiply Extensibly
054xxx 03xxxx RPDE Register Packed Divide Extensibly
054xxx 04xxxx RPA Register Packed Add
054xxx 05xxxx RPS Register Packed Subtract
054xxx 06xxxx RPM Register Packed Multiply
054xxx 07xxxx RPD Register Packed Divide
054xxx 11xxxx RPCL Register Packed Compare Long
054xxx 12xxxx RPMEL Register Packed Multiply Extensibly Long
054xxx 13xxxx RPDEL Register Packed Divide Extensibly Long
054xxx 14xxxx RPAL Register Packed Add Long
054xxx 15xxxx RPSL Register Packed Subtract Long
054xxx 16xxxx RPML Register Packed Multiply Long
054xxx 17xxxx RPDL Register Packed Divide Long
055xxx 01xxxx RCDC Register Compressed Decimal Compare
055xxx 02xxxx RCDME Register Compressed Decimal Multiply Extensibly
055xxx 03xxxx RCDDE Register Compressed Decimal Divide Extensibly
055xxx 04xxxx RCDA Register Compressed Decimal Add
055xxx 05xxxx RCDS Register Compressed Decimal Subtract
055xxx 06xxxx RCDM Register Compressed Decimal Multiply
055xxx 07xxxx RCDD Register Compressed Decimal Divide
055xxx 11xxxx RCDCL Register Compressed Decimal Compare Long
055xxx 12xxxx RCDMEL Register Compressed Decimal Multiply Extensibly Long
055xxx 13xxxx RCDDEL Register Compressed Decimal Divide Extensibly Long
055xxx 14xxxx RCDAL Register Compressed Decimal Add Long
055xxx 15xxxx RCDSL Register Compressed Decimal Subtract Long
055xxx 16xxxx RCDML Register Compressed Decimal Multiply Long
055xxx 17xxxx RCDDL Register Compressed Decimal Divide Long
056xxx 00xxxx SWMDE Swap Medium Decimal Exponent
056xxx 01xxxx CMDE Compare Medium Decimal Exponent
056xxx 02xxxx LMDE Load Medium Decimal Exponent
056xxx 04xxxx AMDE Add Medium Decimal Exponent
056xxx 05xxxx SMDE Subtract Medium Decimal Exponent
056xxx 06xxxx MMDE Multiply Medium Decimal Exponent
056xxx 07xxxx DMDE Divide Medium Decimal Exponent
056xxx 12xxxx LUMDE Load Unnormalized Medium Decimal Exponent
056xxx 14xxxx AUMDE Add Unnormalized Medium Decimal Exponent
056xxx 15xxxx SUMDE Subtract Unnormalized Medium Decimal Exponent
056xxx 16xxxx MUMDE Multiply Unnormalized Medium Decimal Exponent
056xxx 17xxxx DUMDE Divide Unnormalized Medium Decimal Exponent
057xxx 00xxxx SWDDE Swap Double Decimal Exponent
057xxx 01xxxx CDDE Compare Double Decimal Exponent
057xxx 02xxxx LDDE Load Double Decimal Exponent
057xxx 04xxxx ADDE Add Double Decimal Exponent
057xxx 05xxxx SDDE Subtract Double Decimal Exponent
057xxx 06xxxx MDDE Multiply Double Decimal Exponent
057xxx 07xxxx DDDE Divide Double Decimal Exponent
057xxx 12xxxx LUDDE Load Unnormalized Double Decimal Exponent
057xxx 14xxxx AUDDE Add Unnormalized Double Decimal Exponent
057xxx 15xxxx SUDDE Subtract Unnormalized Double Decimal Exponent
057xxx 16xxxx MUDDE Multiply Unnormalized Double Decimal Exponent
057xxx 17xxxx DUDDE Divide Unnormalized Double Decimal Exponent
060xxx 00xxxx SWFRC Swap Floating Register Compressed
060xxx 01xxxx CFRC Compare Floating Register Compressed
060xxx 02xxxx LFRC Load Floating Register Compressed
060xxx 04xxxx AFRC Add Floating Register Compressed
060xxx 05xxxx SFRC Subtract Floating Register Compressed
060xxx 06xxxx MFRC Multiply Floating Register Compressed
060xxx 07xxxx DFRC Divide Floating Register Compressed
060xxx 12xxxx LUFRC Load Unnormalized Floating Register Compressed
060xxx 14xxxx AUFRC Add Unnormalized Floating Register Compressed
060xxx 15xxxx SUFRC Subtract Unnormalized Floating Register Compressed
060xxx 16xxxx MUFRC Multiply Unnormalized Floating Register Compressed
060xxx 17xxxx DUFRC Divide Unnormalized Floating Register Compressed
061xxx 04xxxx AFRCH Add Floating Register Compressed Humanized
061xxx 05xxxx SFRCH Subtract Floating Register Compressed Humanized
061xxx 06xxxx MFRCH Multiply Floating Register Compressed Humanized
061xxx 07xxxx DFRCH Divide Floating Register Compressed Humanized
062xxx 00xxxx SWDRC Swap Double Register Compressed
062xxx 01xxxx CDRC Compare Double Register Compressed
062xxx 02xxxx LDRC Load Double Register Compressed
062xxx 04xxxx ADRC Add Double Register Compressed
062xxx 05xxxx SDRC Subtract Double Register Compressed
062xxx 06xxxx MDRC Multiply Double Register Compressed
062xxx 07xxxx DDRC Divide Double Register Compressed
062xxx 12xxxx LUDRC Load Unnormalized Double Register Compressed
062xxx 14xxxx AUDRC Add Unnormalized Double Register Compressed
062xxx 15xxxx SUDRC Subtract Unnormalized Double Register Compressed
062xxx 16xxxx MUDRC Multiply Unnormalized Double Register Compressed
062xxx 17xxxx DUDRC Divide Unnormalized Double Register Compressed
063xxx 04xxxx AFDCH Add Double Register Compressed Humanized
063xxx 05xxxx SFDCH Subtract Double Register Compressed Humanized
063xxx 06xxxx MFDCH Multiply Double Register Compressed Humanized
063xxx 07xxxx DFDCH Divide Double Register Compressed Humanized
064xxx 00xxxx SWQRC Swap Quad Register Compressed
064xxx 01xxxx CQRC Compare Quad Register Compressed
064xxx 02xxxx LQRC Load Quad Register Compressed
064xxx 04xxxx AQRC Add Quad Register Compressed
064xxx 05xxxx SQRC Subtract Quad Register Compressed
064xxx 06xxxx MQRC Multiply Quad Register Compressed
064xxx 07xxxx DQRC Divide Quad Register Compressed
064xxx 12xxxx LUQRC Load Unnormalized Quad Register Compressed
064xxx 14xxxx AUQRC Add Unnormalized Quad Register Compressed
064xxx 15xxxx SUQRC Subtract Unnormalized Quad Register Compressed
064xxx 16xxxx MUQRC Multiply Unnormalized Quad Register Compressed
064xxx 17xxxx DUQRC Divide Unnormalized Quad Register Compressed
065xxx 04xxxx AFDCH Add Quad Register Compressed Humanized
065xxx 05xxxx SFDCH Subtract Quad Register Compressed Humanized
065xxx 06xxxx MFDCH Multiply Quad Register Compressed Humanized
065xxx 07xxxx DFDCH Divide Quad Register Compressed Humanized
066xxx 00xxxx SWNFRC Swap Numerical Floating Register Compressed
066xxx 01xxxx CNFRC Compare Numerical Floating Register Compressed
066xxx 02xxxx LNFRC Load Numerical Floating Register Compressed
066xxx 04xxxx ANFRC Add Numerical Floating Register Compressed
066xxx 05xxxx SNFRC Subtract Numerical Floating Register Compressed
066xxx 06xxxx MNFRC Multiply Numerical Floating Register Compressed
066xxx 07xxxx DNFRC Divide Numerical Floating Register Compressed
066xxx 10xxxx SWNDRC Swap Numerical Double Register Compressed
066xxx 11xxxx CNDRC Compare Numerical Double Register Compressed
066xxx 12xxxx LNDRC Load Numerical Double Register Compressed
066xxx 14xxxx ANDRC Add Numerical Double Register Compressed
066xxx 15xxxx SNDRC Subtract Numerical Double Register Compressed
066xxx 16xxxx MNDRC Multiply Numerical Double Register Compressed
066xxx 17xxxx DNDRC Divide Numerical Double Register Compressed
067xxx 00xxxx SWNQRC Swap Numerical Quad Register Compressed
067xxx 01xxxx CNQRC Compare Numerical Quad Register Compressed
067xxx 02xxxx LNQRC Load Numerical Quad Register Compressed
067xxx 04xxxx ANQRC Add Numerical Quad Register Compressed
067xxx 05xxxx SNQRC Subtract Numerical Quad Register Compressed
067xxx 06xxxx MNQRC Multiply Numerical Quad Register Compressed
067xxx 07xxxx DNQRC Divide Numerical Quad Register Compressed
077xxx 04xxxx AEQ Add Extensibly Quad
077xxx 05xxxx SEQ Subtract Extensibly Quad
077xxx 06xxxx MEQ Multiply Extensibly Quad
The opcodes for the unaligned load/store instructions are:
142xx0 UALH Unaligned Load Halfword 143xx0 UASTH Unaligned Store Halfword 144xx0 UAL Unaligned Load 145xx0 UAST Unaligned Store 146xx0 UALL Unaligned Load Long 147xx0 UASTL Unaligned Store Long 150xx0 UALM Unaligned Load Medium 151xx0 UASTM Unaligned Store Medium 152xx0 UALF Unaligned Load Floating 153xx0 UASTF Unaligned Store Floating 154xx0 UALD Unaligned Load Double 155xx0 UASTD Unaligned Store Double 156xx0 UALQ Unaligned Load Quad 157xx0 UASTQ Unaligned Store Quad
The opcodes for the scratchpad load/store instructions are:
042xx0 SLH Scratchpad Load Halfword 043xx0 SSTH Scratchpad Store Halfword 044xx0 SL Scratchpad Load 045xx0 SST Scratchpad Store 046xx0 SLL Scratchpad Load Long 047xx0 SSTL Scratchpad Store Long 050xx0 SLM Scratchpad Load Medium 051xx0 SSTM Scratchpad Store Medium 052xx0 SLF Scratchpad Load Floating 053xx0 SSTF Scratchpad Store Floating 054xx0 SLD Scratchpad Load Double 055xx0 SSTD Scratchpad Store Double 056xx0 SLQ Scratchpad Load Quad 057xx0 SSTQ Scratchpad Store Quad
It is intended that the 64 scratchpad registers can be used to keep values with which a program is currently working, so that references to memory can be kept to a minimum. Thus, although memory-reference instructions also include arithmetic operations, unlike the case on a RISC architecture, the motivation behind a load/store architecture is still accepted as valid.
In the instruction mnemonics, "Long" refers to 64-bit integers, "Medium" to 48-bit floating-point numbers, "Floating" to 32-bit single-precision floating-point numbers, and "Quad" to 128-bit extended-precision floating-point numbers.
Integer operations working with long, or 64-bit integers, have as their destination a pair of registers, beginning with an even-numbered register. The location of an operand in memory can begin with any byte, as addresses are byte addresses, but there may be a performance penalty if an operand is fetched from an unaligned location. In the case of floating-point numbers of the medium type, 48 bits in length, an aligned operand is one that begins on the boundary of a unit of 16 bits; for other types, an aligned operand is one whose address is an integer multiple of its length in bytes, so that all memory could be evenly divided into units of that length with no bytes left over at the beginning or the end. Note that it may be attempted by an implementation to fetch more than 16 bits of a medium floating-point number in a single operation, in which case a performance penalty may be experienced on aligned operands on this type which cross a block boundary; the rules for this would be both more complicated and implementation-dependent.
For integers shorter than 32 bits, the insert and unsigned load instructions are used as possible alternatives to the load instruction. The difference between the three instructions is as follows:
The load instruction performs sign extension. A quantity loaded into a 32-bit register is loaded into its rightmost, or least significant, bits, and the first bit of that quantity is also used as the value to which to set all the bits to the left of those filled by the quantity. This ensures that a negative number represented in a variable occupying less than 32 bits of memory is converted to the same negative number in 32-bit form.
The unsigned load instruction fills the bits to the left of the number with zeroes. This allows using variables to represent positive numbers only, and recovering the use of the first bit to allow larger positive numbers to be represented.
The insert instruction does not alter the bits to the left of the number. This allows a 32-bit number to be built up out of smaller pieces.
Other instructions that may need some explanation are as follows:
The compare instruction sets certain status bits in the same way that an ideal subtraction would set them. That is, the status bits indicate "negative" if the destination is less than the source, "zero" if they are equal, and "positive" if the destination is larger than the source, even if performing an actual subtraction for the same argument type would result in an overflow.
The unsigned compare instruction treats its operands as unsigned numbers, since this makes a difference in what the result of a comparison would be, even though two's complement representation means that a subtraction produces the same resulting pattern of bits in both cases.
The multiply extensibly instruction has a destination which is as long as the source on entry, but twice as long as its source on exit. This means that it produces a double-length product of two values, allowing it to be used in performing multi-precision arithmetic.
The divide extensibly instruction has a destination which is twice as long as the source on entry, and which consists of two consecutive registers, or groups of registers, the first twice as long as the source, and the second as long as the source, on exit. It divides the destination by the source, and places the quotient in the first part of the destination, while leaving the remainder in the second, shorter, part of the destination.
Note that because not only the dividend, but also the quotient, is twice as long as the divisor and the remainder with this instruction, the condition known as a "divide check", where a large dividend and a small divisor results in a quotient that will not fit into the result field on exit cannot occur.
The other instructions are self-explanatory.
The swap instruction exchanges the contents of the source and destination.
Add, subtract, multiply, and divide perform the indicated operation, producing results of the same type as their operands.
AND, OR, and XOR perform the basic logical operations:
a b a AND b a OR b a XOR b -------------------------------------- 0 0 0 0 0 0 1 0 1 1 1 0 0 1 1 1 1 1 1 0
in a bitwise fashion on their operands, storing the result in the destination.
A store instruction takes the value at the location specified by the destination field, and stores it at the location specified by the source field. By reversing the normal uses of destination and source, it allows values in registers to be written back out to memory.
Not all the possible combinations of the bits shown above are valid instructions. The Insert and Unsigned Load instructions only apply to byte and halfword operands. Also, Multiplication and division are not provided for byte operands. Instead, the instruction that would have been Divide Extensibly Byte is Store if Greater Byte: this instruction compares the destination byte (which is in a register) to the source byte (which may be in memory), and if the source byte is less than the destination byte, the byte at the destination is copied to the source location, overwriting its contents. This specialized instruction is used to allow semaphores to be used to control the sharing of resources between processes.
When the computer is operating on floating-point numbers in IEEE 754 format, these instructions are, of course, not available, since the leading 1 bit of the mantissa is suppressed, which requires that the number must be normalized, except in the special case of gradual underflow.
However, this architecture offers the option of changing the mode of floating-point operation to use other floating-point formats, in which numbers may generally be represented in an unnormalized form.
Unnormalized add or subtract instructions operate by first aligning the operand with the lower exponent with the other operand, and then performing the addition or subtraction on the mantissa portion of the arguments. If a carry out of the mantissa results, a single right shift, with adjustment of the exponent, is performed; otherwise, no repositioning of the mantissa is performed.
Unnormalized multiply or divide instructions produce a result which has either as many leading zeroes as or one less leading zero than that of the operand with the greater number of leading zeroes, so as to correctly indicate the significance of the result. The number of leading zeroes will be the same if the mantissa of the result is equal to or greater than the mantissa of the operand with the greater number of leading zeroes (in the case where both operands have the same number of leading zeroes, if the mantissa of the operand is equal to or greater than the mantissas of both operands), and it will be one less otherwise. Thus, these instructions, unlike the unnormalized add and subtract instructions, do not work by merely omitting a postnormalization step; instead, they are specifically designed to support significance arithmetic.
Significance arithmetic is one method of allowing a computer to keep track of ongoing errors in a calculation. Other methods of doing this are also available, significance arithmetic is considered by some to be flawed, and at least one of the other methods of doing this, interval arithmetic, tends to be acknowledged as having a somewhat greater degree of mathematical validity than significance arithmetic, although it, too, is considered to be of limited benefit rather than approaching the effectiveness of a panacea in this area. Despite the fact that these concerns have some validity, the simple form of significance arithmetic that can be obtained through unnormalized arithmetic is considerably more amenable to a hardware implementation than most other possible methods. The IBM 7030, or STRETCH, had an option of adding a constant value, termed a noise value, to the last bits of floating-point numbers; thus, this option was equivalent to the method, available today on IEEE-754-compliant systems today of running the same program with different rounding modes selected, although it resembles a different proposed method, of appending random noise bits to the ends of floating-point numbers. The major limitation of significance arithmetic is that it will indicate when precision is lost in an individual step of a calculation, but it will not indicate how error accumulates due to the involvement of a large number of quantities of limited accuracy in a calculation. This limitation is not entirely a bad thing, as it does not prevent significance arithmetic from pointing out correctable deficiencies in programs, while still permitting that form of arithmetic to be used even with computations such as simulations, from which useful data can be obtained, even though the final "result", in the sense of the state of the system, is nonsense. That is, a simulation of the Earth's atmosphere can still be used to learn general facts about how different types of weather systems behave, even if it is allowed to run past the amount of simulated time for which it could, if loaded with the actual present state of the Earth's atmosphere, yield accurate weather forecasts. (A full discussion of chaos theory is beyond the scope of this section.) |
Note that there is one circumstance under which an unnormalized arithmetic instruction will not retain significance, but will instead post-normalize despite the fact that this will indicate the presence of nonexistent significance in this number: that is when the result is near the upper end of the valid exponent range, and an unnormalized result would lead to exponent overflow.
The unnormalized multiply extensibly and divide extensibly instructions behave like the analogous operations on integers, where the mantissa portions of the arguments are the integers, and the exponents are adjusted so as to indicate the numerical magnitude of the result. Where numbers occupying a pair of registers are generated, both have an exponent part, and the difference between the two exponents reflects the precision of the floating-point type in use. Fixed-point overflow of the exponent is allowed and ignored, and, where a special value of the exponent is used to indicate symbols representing "not-a-number" (NaN) values, that value is skipped. (This would include the exponent value used in the representation of zero in the Standard format, but unnormalized operations are, of course, not defined for that format.)
Unlike the integer multiply extensibly and divide extensibly instructions, their operands always consist of multiple registers at the given precision; a double-length operand is never a single register at a higher precision. Thus, these instructions always behave like Multiply Extensibly and Divide Extensibly, never like Multiply Extensibly Halfword and Divide Extensibly Halfword, even when the basic type does not have the full 128-bit length of a floating-point register.
In an unnormalized multiply extensibly instruction, if the destination is in register N, the product is in registers N and N+1; register N+1 contains an exponent equal to the sum of the exponents of the arguments, and register N has an adjusted exponent which may be incorrect if a fixed-point overflow took place.
In an unnormalized divide extensibly instruction, when the destination field of the instruction specifies register N, the dividend is in register N and N+1, and the exponent in register N is the one considered as being valid; after the operation, registers N and N+1 contain the quotient, which is not rounded, unlike the result of a regular unnormalized divide instruction, and register N+2 contains the remainder.
It is these instructions, rather than the simple multiply unnormalized and divide unnormalized instructions, that work by omitting postnormalization, because their purpose is to facilitate software multi-precision floating-point operations.
The Multiply Extensibly Unnormalized and Divide Extensibly Unnormalized instructions are unavailable, even though the other unnormalized operations are available, with the Modified Comprehensive, Modified Standard, and Modified Native formats. However, if neither Extremely Gradual Underflow nor Extremely Gradual Overflow is enabled, they are available, along with the other unnormalized operations, for the Native format, and if these features, and Hyper-Gradual Overflow and Hyper-Gradual Underflow as well are all turned off, they are also available, along with the other unnormalized operations, for the Comprehensive format.
Note that there are no unnormalized single-operand instructions. Dividing a number by itself will provide a one with the same number of significant digits as the original number, and this can be multiplied by the result of a conventional single-operand instruction to produce a result with the desired significance. This technique is, however, not applicable to all the single-operand instructions; the logarithm function is an obvious case where a special rule applies to the number of significant bits in the logarithm of a number with a given number of significant bits.
As contrasted with the MEUQ instruction, the MEQ instruction does not omit postnormalization. Its purpose is specifically to facilitate work with 256-bit floating point numbers composed of two 128-bit extended-precision floating point numbers.
There are also AEQ and SEQ instructions which place the sum of two 128-bit extended-precision floating-point numbers in two consecutive registers containing two 128-bit extended-precision floating-point numbers with offset exponents.
These three instructions work in the same fashion as the add, subtract, and multiply instructions which were provided on the IBM 704 computer and its successors, facilitating double precision in software.
The more straightforwards operate instructions will be discussed in the next section, such as the jump instruction and memory-reference instructions for packed decimal and character-string types.