Recently, I ran across an open-source Chess program that is able to play a lot of chess variants. (The particular program in question was ChessV 2.2, if you are interested.)
However, it didn't support any form of Hexagonal Chess.
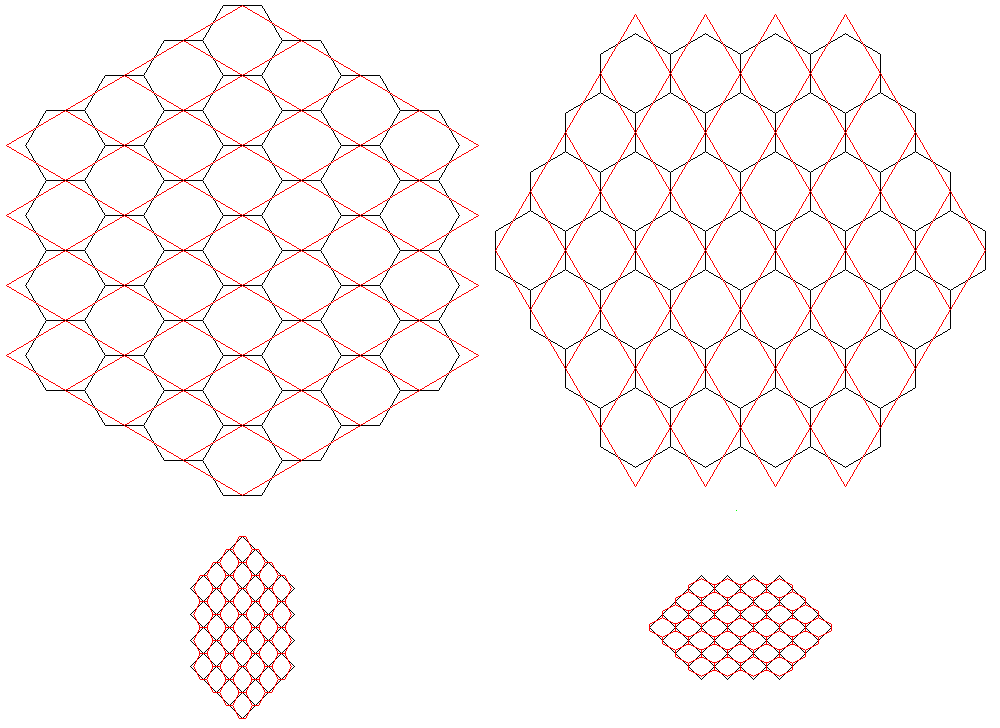
After a little thought, I realized that it's easy enough to set up a correspondence between the locations for pieces on a hexagonal chessboard, and the Cartesian grid that is easier for computers to work with. The diagram below illustrates this:

On the left, one sees how a hexagonal board of the first type, such as used for Gliński hexagonal chess, could be made to correspond to a board the spaces of which are squares. And on the right, one sees how a hexagonal board of the second type, such as used for the chess variant due to Wellisch, could be made to correspond to a board with squares for spaces - basically, in exactly the same way, but with everything rotated by 90 degrees.
However, a chess board oriented diagonally doesn't really correspond well to an array in a computer - unless one only uses half the cells in the array. This is done, as the waste of memory is inconsiderable, by many programs for playing checkers, instead of wrestling with program code that requires the programmer to have a mental model of the checkerboard too far removed from an actual checkerboard in the real world.
Maybe that's what should also be done when implementing hexagonal chess on a computer, for the same reason.
But I thought that it was better to use all the available spaces, since otherwise bugs could be introduced by the programmer accidentally placing pieces on hexes that don't really exist.
So as the hexagonal board on the right could be obtained from the hexagonal board on the left by rotating it clockwise by 30 degrees, I obtained an intermediate board through rotating the board on the left clockwise by 15 degrees, as shown in the upper left corner of the diagram below:
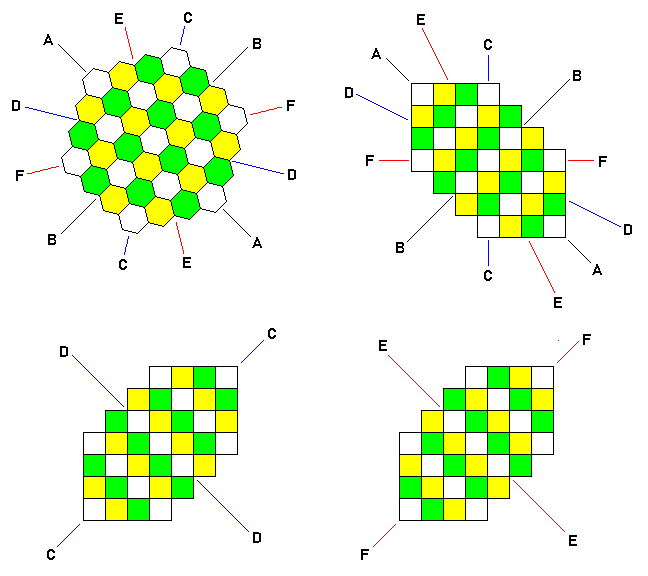
The intermediate board is shown in the center of the diagram, at the top. It has six axes of symmetry, and all six of them are labelled, with letters from A through F.
At the bottom of the diagram, on the left and right, we see my initial concept of an intermediate board, this time resulting from the board on the left being rotated clockwise by 45 degrees.
In the case of a Hexagonal Chess variant of the type shown on the left of the first image, the relationship between the colored hexagonal board in the top left of the current image and the rectangular array is shown by the diagram on the bottom left of the current image; symmetry axis C of the hexagon corresponds to the vertical direction on the hexagonal board, and to one of the diagonals of the array.
Symmetry axis D of the hexagon corresponds to the horizontal direction on the hexagonal board, and to the opposite diagonal of the array.
So the important symmetries of the hexagonal board are mapped to important symmetries of the square array.
In the case of a Hexagonal Chess variant of the type shown on the right of the first image, the relationship between the colored hexagonal board in the top left of the current image and the rectangular array is shown by the diagram on the bottom right of the current image; symmetry axis E of the hexagon corresponds to the vertical direction on the hexagonal board, and to one of the diagonals of the array.
Symmetry axis F of the hexagon corresponds to the horizontal direction on the hexagonal board, and to the opposite diagonal of the array.
Since the same diagonals on the two rectangular arrays are marked D and C or E and F respectively, but these are different symmetry axes of the hexagon at the top, the correspondence between squares and hexagons in the two cases is different, and this results in a difference in how the squares are colored in the two diagrams of the rectangular arrays in the bottom row of the current image.
On the top right of the current image is a later thought I came up with. It has the advantage that the degree of rotation between the hexagonal diagram at the top and the rectangular array below it is less, and it also has the advantage that the correspondence between hexagons and square cells is the same for either board orientation.
It has the disadvantage, though, that now the horizontal and vertical axes of the board, in either orientation, don't correspond to natural symmetry axes of the rectangular array in all cases.
Axis C corresponds to an orthogonal line in the rectangular array, and axis F corresponds to the other orthogonal line in the rectangular array, so one of the axes of symmetry that is used for each board orientation does have a simple equivalent.
But the other two axes used, one in each case, axis D and axis E, correspond to lines in a direction that can result from repeating the same Knight move. This is harder to keep clear in one's mind, either when defining the displacements for each piece type (although if the moves of the piece are symmetrical, the displacements in the square array will be the same, but because of the different order in which one examines the six hexagonal directions, it can still be harder to see) or even when carrying out the simpler task of setting up the initial array of the pieces.
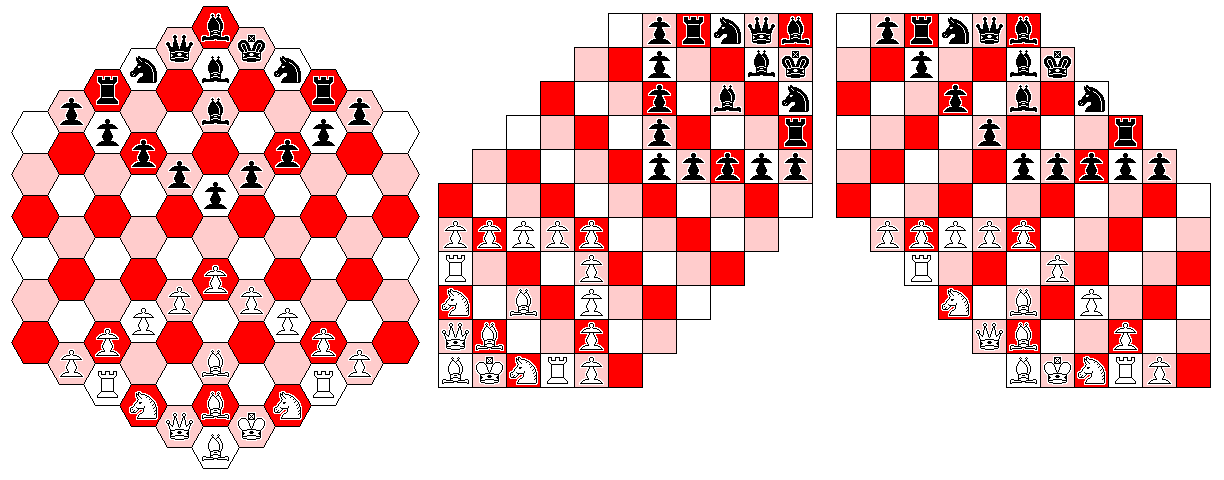
The issue involved may be made clearer by the image above, which gives the concrete example of how the initial array for Gliński hexagonal chess, as depicted at left, would be represented in the two cases.
In any case, care and attention will be needed by the programmer. A hexagonal board has three orthogonal axes; when it is represented in a square grid, two of those axes are mapped to orthogonal axes, and one of them is mapped to a diagonal axis.
But in the case of my first concept, as shown in the second diagram, because the vertical (orthogonal) axis of the hexagonal board, and the horizontal (diagonal) axis of the hexagonal board are both mapped t diagonal axes of the square grid, the symmetry (except for the King and Queen) around the vertical axis of the hexagonal array are retained on the square grid, as a symmetry around the diagonal axis to which the vertical axis of the hexagonal board is mapped.
The second diagram, though, shows that in this mapping, the vertical and horizontal symmetries of the hexagonal board are lost, making it harder to visualize the hexagonal board from the square array while working with the latter.
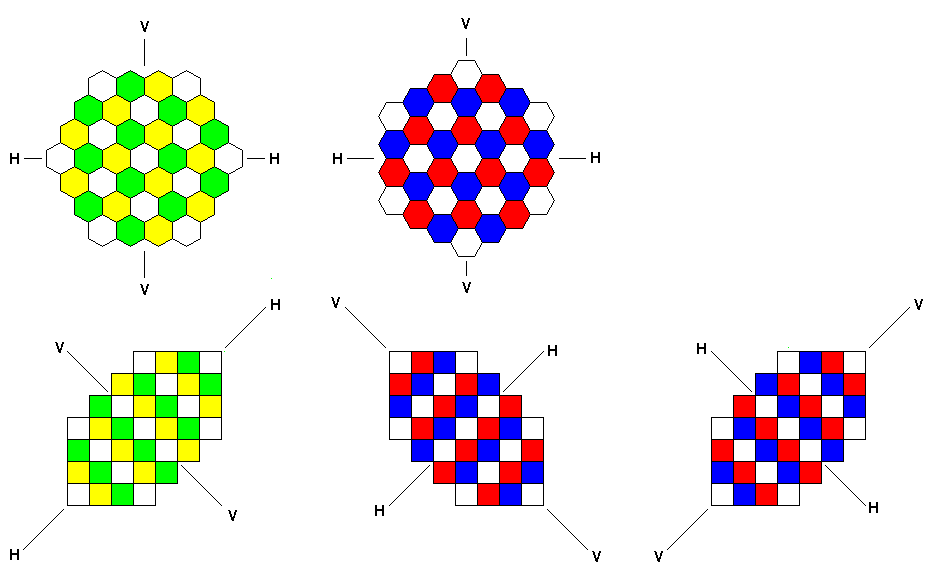
One other issue needs to be addressed. The diagram above illustrates what seems to be an even simpler idea; here, the mapping of the horizontal and vertical directions to the two diagonals remains constant, reducing the possibility of confusion, if we look at the four diagrams on the left and in the center of the diagram above.
The only thing that changes is which diagonal is stretched on the way to the hexagon, so the relationship between the two types of Hexagonal Chess is the same as with the diagonal board as shown on the left and right edges of the earlier diagram.
Why couldn't this mapping convention be used for a chess program?
Well, for ChessV in particular, but likely for many other chess programs as well, since changing the stretch means changing the local mapping between a square and adjacent squares, versus the local mapping between a hexagon and adjacent hexagons, this means that it's no longer possible to use the same definiton of the possible displacements for a piece, on the square grid, for the two orientations of the hexagon, even when the move of the piece is symmetric in all six directions on the hexagonal board.
To avoid that, my original idea, illustrated by the diagram in the lower right of the image, which swaps the diagonals used for the horizontal and vertical in the other case, needs to be used instead.