
Aside from squares and hexagons, there is one other simple way to tesselate the plane:

There have been occasional proposals for versions of Chess, Checkers, and war games played on a board of triangles instead of squares or hexagons, but such proposals have been comparatively rare.
Of course, if one plays on only one color of square, as is done when playing Checkers on a normal square board, the result is a board that is isomorphic to a board made of hexagons:
although three of the six sides of each hexagonal space at least look different from the other three sides.
The reason that there haven't been too many chess variants proposed for a board made up of triangles stems from a problem that results from the fact that a triangle has an odd number of sides.
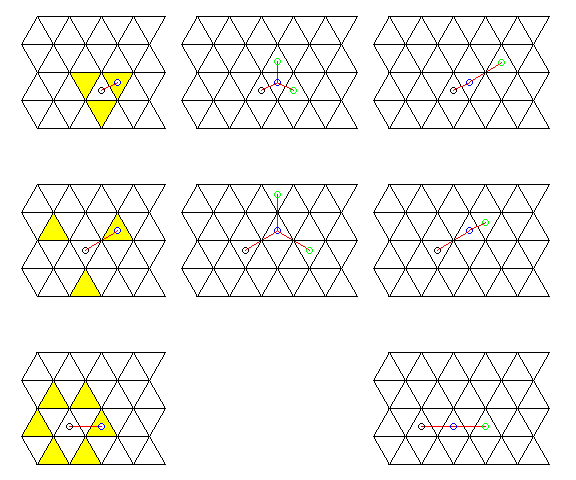
Each triangle has three kinds of immediate neighbor.
If one moves from one triangle to the next by going directly across a side, one can't repeat such a move for a second step and still proceed in the same direction.
The same is true if one moves from one triangle to the next by going directly through a point; again, one has to choose between continuing to move in the same direction, or continuing to make the same kind of move, for a second step.
Thus, in order to demonstrate the self-unpin in a chess variant without changing the board to the anchor-ring (or toroidal) configuration, when I devised the Rhinoceros, which went around in circles, I had to have it alternate between orthogonal and diagonal steps.
On the board composed of triangles instead of squares, pieces naturally go around in circles, and in order to make them go in straight lines, it is necessary to have the types of steps they take alternate.
However, in the third case of the immediate neighbors of a triangle, moving obliquely to a triangle which is neither directly across a line or directly through a point, it is possible to move in a straight line while repeating the same kind of step.
However, there is a third possibility:

Instead of repeating the same type of move with a course change in the same direction each time, leading to moving around in circles, or alternating types of move in order to move in a straight line, one could repeat the same type of move, but alternate the direction of the course changes, in order to achieve movement which is along a path with an overall straight-line direction.
This is particularly attractive in the case of a piece that moves across the sides of the triangle, because that then leads to a piece which has enough density of coverage to be as effective in inflicting checkmate as the Rook is in conventional Chess.