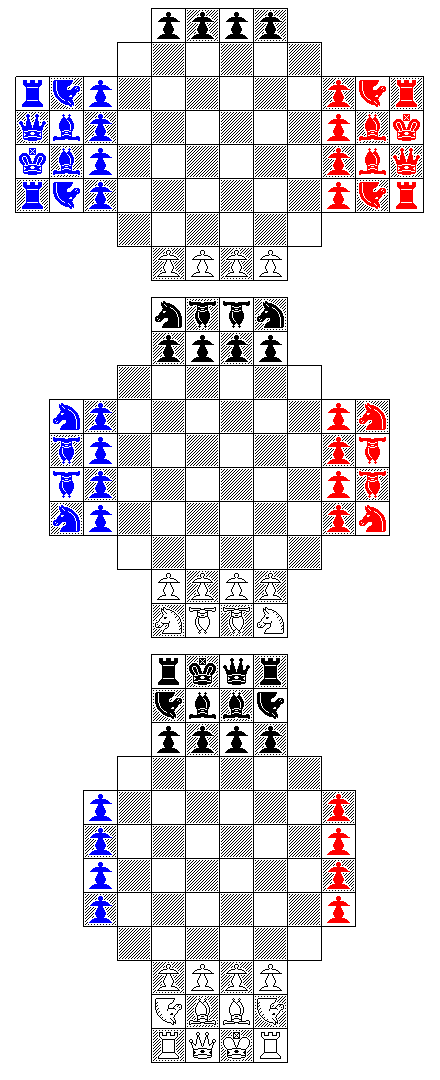
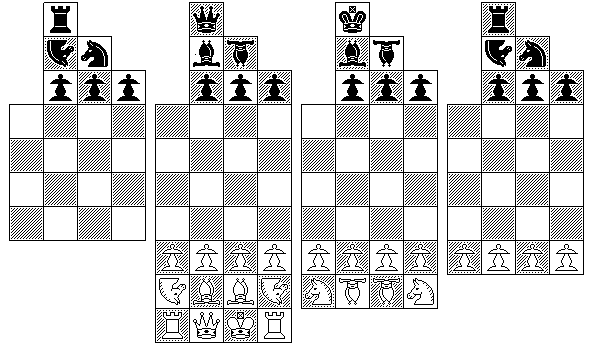
The diagram at right shows the layout I propose for three-dimensional Chess.
Many types of three-dimensional chess have been proposed. I have devoted some thought to the difficulties that making a practical version of three-dimensional chess presents, and to the characteristics of the different versions, and have embodied my conclusions in the layout shown.
One problem presented by three-dimensional chess is that of being able to easily reach all the levels of the board, and yet having sufficient space between them to reach in to each one. Hence, it is important to limit the number of levels used. Thus, I designed my version to use only three levels.
As I wished to make my version of three-dimensional chess as much like the ordinary version of chess as possible, I wanted to have a solid wall of pawns in front of the pieces of each side. I achieved this, as you can see in the diagram, by having the edge of the board staggered from one level to the next: three rows of pawns, one on top of each other, are in front, with first two rows of pieces, and then one row of pieces, behind them.
Note that a smaller board than that shown, consisting of only the central four files of each level, is possible. In that case, it would make sense for the black pieces to be arranged three rows deep on the top level instead of the bottom level, and for the kings and queens of both sides to face each other on the same file. Shortening each level by two ranks would also be reasonable. However, the illustration would be harder to understand, as it would be less clear how the boards should be stacked one atop the other.
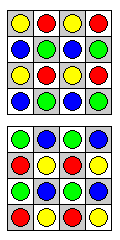
Thus, I chose to illustrate a board that can also be used, as the red and blue chessmen at the sides show, for a four-handed game. The corners of the 6 x 6 central area of the board are to be directly above each other, and the larger board does give pieces extra room to move.
The version played on this board I will term 3D Wing Table Chess, to give it a distinctive name.
The upside-down Knights here symbolize a piece I will call the Airman (the name Balloon being taken for the fourth-dimensional successor to the Bishop and Unicorn, and Pegasus being a proper name). This piece will be a 1-2-2 leaper. (A 1-1-2 leaper and a 1-2-3 leaper, two other possibilities for a three-dimensional analogue of the Knight, always remain confined to one color of square.)
The squares it can jump to are shown below:
- - - a a - - - a a - - - a - - a - - - - - - - - a - - a - - - - - - A - - - - - - a - - a - - - - - - - - a - - a - - - a a - - - a a - - -
The upside-down bishops represent Unicorns, the standard three-dimensional version of the Bishop in Fairy Chess.
Their move is as illustrated below:
b - b - - - - - - - b - b - - - b - b - - - - b - b - - - - - - - - - B - - - - - - - - - b - b - - - - b - b - - - b - b - - - - - - - b - b
Note that the Unicorn switches from light to dark squares as it passes between adjacent levels. On the other hand, the conventional light and dark chequering of the squares is appropriate for the three-dimensional Bishop. To allow the Unicorn's move to be easily followed, a different color scheme, involving four colors, is required. The following diagram shows two 4 x 4 levels, one above the other, each with a central circle; outside the circle, they are colored white and gray, to indicate where the Bishop may move, and within the circle, they are colored yellow, green, blue, and red to indicate the moves of the Unicorn.

Since it takes four Unicorns to reach every square on the board, and, as well, the Airman is perhaps a somewhat awkward piece to use, especially on a board with less than five levels, perhaps an alternate version of the initial array might be preferred, in which the Airmen are removed, and there are four Unicorns on each side instead. The diagram below illustrates the to arrays side by side, the original one used in the other diagrams here on the left, and the alternative array on the right.

I suspect the alternate array may well be the preferred array for these games.
And the convenience of using a 5 x 5 x 5 cube to illustrate how pieces move may perhaps partly explain why the Normal Form of three-dimensional chess used for Fairy Chess problems (also known by its German name, Raumschach) uses that board. But the initial layout involves two stacked arrays, with an opening at the top, leading to an important difference from regular chess.
Thus, the Unicorn moves by repeated steps that involve a displacement of 1 in each of the three dimensions.
Another fundamental problem of three-dimensional chess, which it shares with some forms of hexagonal chess, is that it is very difficult to give checkmate. I have decided to deal with that by means of defining the King's move as follows:
Normally, the King can move and capture by moving one step in the directions used by the Rook, Bishop, and Unicorn.
When the King is in check, however, it can only move one step in Rook directions. But it may still capture by moving a single step in Bishop and Unicorn directions, in addition to retaining its ability to capture by moving one step in Rook directions.
While this rule may seem unusual, I feel it will provide a nice balance between King mobility and not making checkmate too difficult to give, or too easy.
Also, out of similar considerations, the Queen has the move of the Unicorn as well of those of the Rook and the Bishop.
The Pawn moves one step forward, as in normal chess, across the board in the direction of the opponent. Its capturing move, however, will be one of the four possible one-step Unicorn moves that are partly in that forwards direction, not one-step Bishop moves. (Incidentally, giving the Pawn this capturing move has the interesting consequence that the Pawns of each side are divided into two distinct groups, so that Pawns can only protect other Pawns in their own group. Thus, in effect, each side has two separate Pawn structures.)
There is no castling. Pawns promote whenever they reach a square at the other end of the board from which no further direct forwards movement is possible, even if that square is not in the opponent's starting area, and even if a capturing move could still be made from the square. There is also no double-step first move for Pawns, and therefore no en passant capture.
Stalemate is scored as in Leaping Bat Chess, as 3/5 of a point for the player forcing stalemate. However, the relevance of this rule may be very limited in this game, as the rule reducing the King's mobility only when in check would seem to imply that stalemate would be harder to give than checkmate under most circumstances. It may well be more appropriate to make stalemate a victory for the attacking player as well, but only extensive experience in actual play could settle that question.
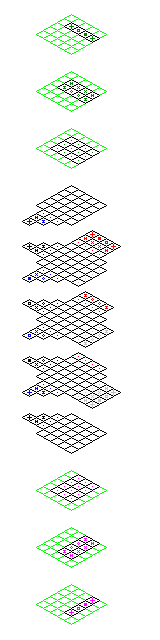
Incidentally, the symmetries of the cube could be used to allow a board with a central 6 x 6 x 6 cube to be used for a three-player game. But this would involve a board nine levels high: only one player would have his pieces aligned as shown in the diagram at right; a second would have the rows of pawns and pieces become vertical columns, and the third would have the three rows of pawns on one level, then two rows of pieces above them, and then one row of pieces at the top.
Here is a picture of a small board with this type of symmetry to illustrate the concept:
From this illustration, we can see that a central 4 x 4 x 4 cube would be workable using the array of twelve pieces shown above, as the extra corner indentation is not needed to keep the arrays of the three players separate. Thus, the three-player version of this board could indeed be practical.
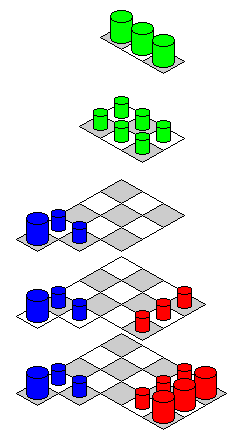
Even the board as shown could be used for some type of game with only two kinds of pieces, with the objective being to capture the opponent's whole force. Perhaps something like this already exists. The fact that each of the three arrays is in a different orientation forces players to think three-dimensionally. Unfortunately, the three sides are in a relationship such that one is, in effect, before, and the other is after, the third player, so the array is not symmetric with only two players. With two players, though, arrays at right angles could be used if they are on opposite cube faces, to have a symmetrical arrangement that encourages three-dimensional thinking.
This picture illustrates the symmetry needed for that arrangement. And here is a layout for a practical board, with four levels instead of three, for a two-player game using the array of pieces introduced on this page:
The game played with this 112-square layout may be called Forced 3D Chess, since, as noted, the fact that the arrays are in different orientations makes it impossible to escape the 3D nature of the game.
Note that on this board, as on the regular Chess board, the Queen takes her own color, instead of all the Queens being on light squares, as is true of most of the other board layouts shown on this page.
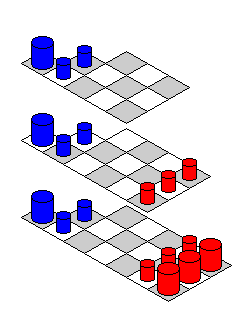
As this is likely the best of the variants, here is a realistic 3-D drawing of the board and pieces,
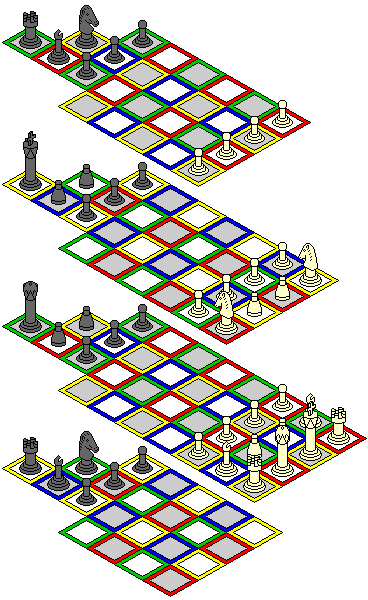
with the alternate layout with four Unicorns employed.
The tall diagram on the right illustrates a board which can be used by two, three, or six players using the symmetries explored here using the array and rules for three-dimensional chess given on this page. The game with this board can be referred to as Triquetral Cube Chess, noting the symmetry of the two groups of arrays involved, the white, blue, and green on the one hand, and the black, red, and yellow (purple on the schematic diagram) on the other.
Because the board is quite large, having eleven levels, the chess pieces are noted in a very schematic manner:
pawn * airman * * *** * * knight *** * *** bishop * * * * * unicorn * * * * rook * * ***** * * king *** * * *** queen *** *** ***
Also, the top and bottom three levels are small rectangles; the green area simply shows where these rectangles stand in relation to the central 5 x 5 square of the five middle levels, so that alignment is unambiguous.
Although a schematic diagram at a very small scale is needed to show the various levels in their proper relation to each other, the levels can be depicted in full size in an image of reasonable size if they are shifted around a bit to squeeze them together. Since Queens of opposite sides face each other on this three-dimensional board, the square on each level in the column where the top and bottom Queens are located (of the green and yellow sides) is outlined in purple in the diagram below, as an aid to aligning the levels:
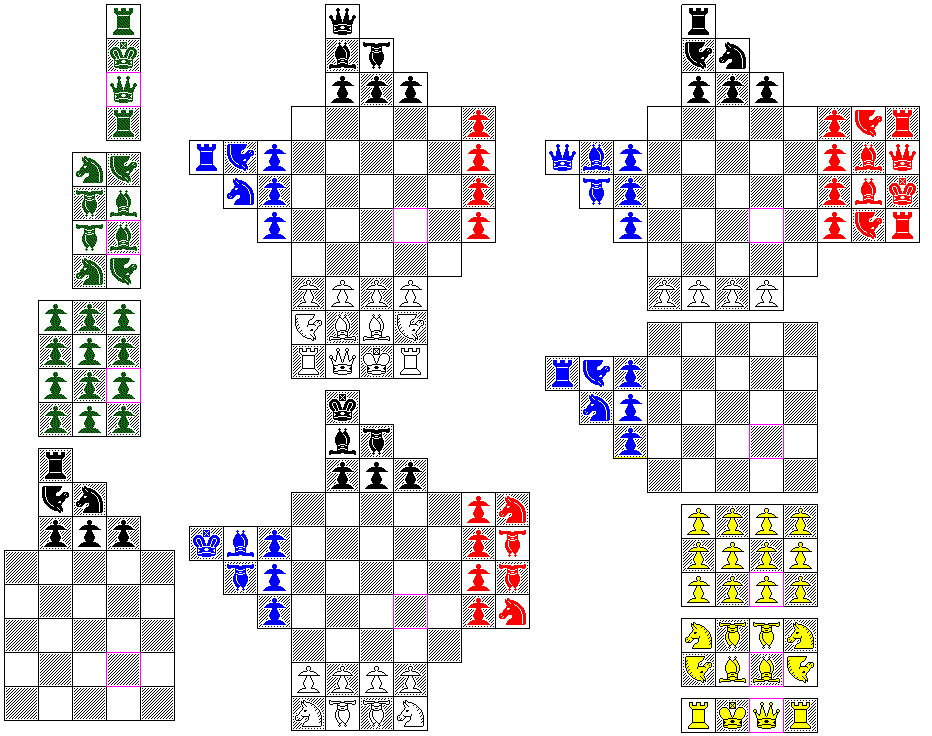
Of course, following the other three-dimensional diagrams above, one can have a board for two-player games only, including only the wings occupied by the white and black pieces, or a board for three-player games only, including only the wings occupied by the white, blue, and green pieces. But to have a board that can be used for both two-player and three-player games, and be symmetrical in both cases, it appears that, if one doesn't want to change the board to play either type of game, or simply remember that certain squares aren't part of the board for the game, the full six-player layout is needed.