
On this page, the original form of Random Variant Chess, originally on the main page of this subsection, is preserved:
The following diagram:

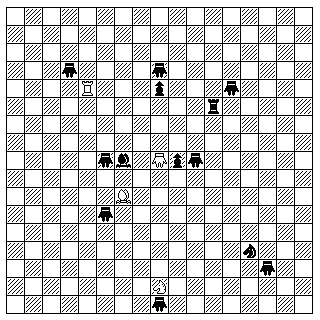
shows the layout of a form of Chess which involves a far more modest augmentation of the board. The rules are as for regular Chess except that the stalemate rule is as for Leaping Bat Chess (the player forcing stalemate gets 3/5 of the point for the game, the other player getting 2/5), and the King moves four squares when castling to Kingside or Queenside, and the moves of the additional pieces used are as described in the rules of Leaping Bat Chess.
Since this was written, I have been inspired by the institution of komidashi in the game of Go to propose what I believe to be a superior scoring scheme, which is discussed at length on a previous page:
| Game Outcome | Points for White | Points for Black |
| White forces checkmate. | 100 | 0 |
| White forces stalemate. | 60 | 40 |
| White bares Black's King | 56 | 44 |
| White gives perpetual check | 52 | 48 |
| Draw | 50 | 50 |
| Black gives perpetual check | 43 | 57 |
| Black bares White's King | 41 | 59 |
| Black forces stalemate. | 39 | 61 |
| Black forces checkmate. | 0 | 100 |
Since this scoring scheme includes bare King as a victory condition, it should be noted that when the last of the opponent's pieces other than the King is captured, a player can say "Continue" if he intends to play for a checkmate - or a stalemate.
This variant retains the symmetry of the opening layout. As you can see in the diagram above, four squares in each player's back rank contain question marks.
Which pieces are to occupy those squares is what is chosen at random in this form of Chess, from the following list of possibilities:
1) Giraffe, Camel; Camel, Giraffe 2) Fers, Camel; Camel, Fers 3) Wazir, Camel; Camel, Wazir 4) Man, Camel; Camel, Man 5) Alfil, Camel; Camel, Alfil 6) Dabbaba, Camel; Camel, Dabbaba 7) Walker, Camel; Camel, Walker 8) Tiger, Camel; Camel, Tiger 9) Rhinoceros, Camel; Camel, Griffin 10) Wazir, Fers; Fers, Wazir 11) Man, Fers; Fers, Man 12) Walker, Fers; Fers, Walker 13) Tiger, Fers; Fers, Tiger 14) Rhinoceros, Fers; Fers, Griffin 15) Man, Wazir; Wazir, Man 16) Walker, Wazir; Wazir, Walker 17) Tiger, Wazir; Wazir, Tiger 18) Rhinoceros, Wazir; Wazir, Griffin 19) Man, Alfil; Alfil, Man 20) Walker, Alfil; Alfil, Walker 21) Tiger, Alfil; Alfil, Tiger 22) Rhinoceros, Alfil; Alfil, Griffin 23) Man, Dabbaba; Dabbaba, Man 24) Walker, Dabbaba; Dabbaba, Walker 25) Tiger, Dabbaba; Dabbaba, Tiger 26) Rhinoceros, Dabbaba; Dabbaba, Griffin 27) Man, Walker; Walker, Man 28) Tiger, Walker; Walker, Tiger 29) Rhinoceros, Walker; Walker, Griffin 30) Tiger, Man; Man, Tiger 31) Rhinoceros, Man; Man, Griffin 32) Rhinoceros, Tiger; Tiger, Griffin 33) Zebra, Camel; Camel, Zebra 34) Zebra, Fers; Fers, Zebra 35) Zebra, Wazir; Wazir, Zebra 36) Zebra, Man; Man, Zebra 37) Zebra, Walker; Walker, Zebra 38) Tiger, Zebra; Zebra, Tiger 39) Rhinoceros, Zebra; Zebra, Griffin 40) Giraffe, Zebra; Zebra, Giraffe 41) Walker, Tiger; Tiger, Walker 42) Man, Tiger; Tiger, Man 43) Zebra, Tiger; Tiger, Zebra 44) Dabbaba, Alfil; Alfil, Dabbaba 45) Man, Fers; Fers, Wazir
Optionally, the first 32 alternatives in the list above can stand on their own as the pool from which to select a variant.
In addition to playing each form of Chess thus randomly selected twice, with one player and then the other as White, the schedule of games is also to be varied so that each player has an equal chance of being the first to play a variant.
Thus, four games between two players would proceed in the fashion:
Game 1: A: White B: Black random variant 1 Game 2: A: Black B: White random variant 2 Game 3: A: White B: Black random variant 2 Game 4: A: Black B: White random variant 1
This pattern, however, when repeated, does still lead to one asymmetry between the two players: A plays, as white, the variant first encountered as black in the next game, while B plays, as white, the variant first encountered as black three games later. As long as there is a pause between pairs of games, however, this asymmetry would not be significant.
Attempting to eliminate this particular asymmetry does not yield an obvious answer, because one player had to play white first; for example, the following scheme:
Game 1: A: White B: Black random variant 1 Game 2: A: Black B: White random variant 2 Game 3: A: White B: Black random variant 2 Game 4: A: Black B: White random variant 1 Game 5: A: White B: Black random variant 3 Game 6: A: Black B: White random variant 3 Game 7: A: White B: Black random variant 4 Game 8: A: Black B: White random variant 4 Game 9: A: White B: Black random variant 5 Game 10: A: Black B: White random variant 6 Game 11: A: White B: Black random variant 6 Game 12: A: Black B: White random variant 5
although it allows A and B both to play first as White with a new variant when it is played twice in succession an equal number of times, finds A playing first as White for both variants 1 and 5; changing from the first to the last of a group of three games does not change who plays first.
One way to solve the problem is for player A to play Black first for the last six games, so that player A would play: WBWBWBBWBWBW. But would that be fair?
And then I remembered how one way to minimize White's advantage from moving first would be to have white move once for the first turn, and then for each player to make two moves per turn afterwards. Thus, a very simple possibility exists:
Game 1: A: White B: Black random variant 1 Game 2: A: Black B: White random variant 1 Game 3: A: Black B: White random variant 2 Game 4: A: White B: Black random variant 2 Game 5: A: White B: Black random variant 3 Game 6: A: Black B: White random variant 3
and so on, with each player taking White for two games in a row, except that the players alternate colors after the first game.
Should, however, 45 possibilities be deemed insufficient, another method of randomizing the variant in use is provided, which offers more variations. Extended Random Variant Chess requires that several more pieces be defined, as follows:
The Empress (also known as the Chancellor) moves as either the Rook or the Knight.
The Princess (also known as the Archbishop) moves as either the Bishop or the Knight.
The Cannon (also known as the Pao) moves as a Rook, but when capturing, must jump over exactly one piece of either color to reach the piece to be captured, on any square beyond it.
The Leo moves as a Queen, but follows the same rule for capturing as the Cannon. (That is, the rule about jumping over one piece to capture, but that rule is applied to it's own move along Queen lines.)
The Vao moves as a Bishop, but follows the same rule for capturing as the Cannon. (Again, although like the Cannon it captures by leaping over another piece, it still captures along Bishop lines, unlike the Cannon.)
The Grasshopper moves, and captures, on the square immediately beyond the nearest piece of either color in any of the eight directions in which a Queen moves. Thus, the eight spaces to which the white Grasshopper in the center of the board in this diagram can move to are those which contain black Grasshoppers.
The Archer moves, but does not capture, as a Man, and captures (and gives check), but does not move without capturing, as a Knight.
The Sprinter moves, but does not capture, as a Giraffe, and captures (and gives check), but does not move without capturing, as a Man: to any immediately adjacent square, diagonally or orthogonally.
The Star moves and captures as either a Wazir or an Alfil; that is, it can move one space orthogonally, or two spaces diagonally.
Given these extra pieces, the choice of a random variant from the larger pool for Extended Random Variant Chess may proceed in one of two ways:
The first method (yielding General Extended Random Variant Chess) begins with this step:
It is chosen at random for the Queen to be replaced by one of:
1) a Queen (that is, left alone) 2) a Griffin 3) a Rhinoceros 4) an Empress 5) a Leo
It is chosen at random for the two Bishops to both be replaced by a pair of:
1) Bishops (that is, left alone) 2) Tigers 3) Sprinters 4) Vaos
It is chosen at random for the two Rooks to both be replaced by a pair of:
1) Rooks (that is, left alone) 2) Princesses 3) Cannons
It is chosen at random for the two Knights to both be replaced by a pair of:
1) Knights (that is, left alone) 2) Men 3) Zebras 4) Archers 5) Stars 6) Grasshoppers
As an example of General Extended Random Variant Chess, here is what the array would become if the following random selection of a variant took place:
Queen: 5) Replaced by Leo Bishops: 2) Replaced by Tigers Rooks: 3) Replaced by Cannons Knights: 1) Left as Knights Variant: 32) Rhinoceros, Tiger; Tiger, Griffin
Since the Bishops were replaced by Tigers, the Tigers in the variant are replaced by Vaos, and the pieces on the back rank are:
Cannon, Rhinoceros, Vao, Knight, Tiger, Leo, King, Tiger, Knight, Vao, Griffin, Cannon
as shown in the diagram below:

Note that in this diagram, a circled G replaces the symbol used on the previous page for the Griffin; that makes that symbol available to represent the Leo, to correspond with analogous symbols representing the Vao and the Cannon.
The second method (yielding Restricted Extended Random Variant Chess) proceeds as follows:
A piece substitution is chosen at random from the following list:
1) No substitutions. 2) Griffin replaces Queen. 3) Rhinoceros replaces Queen. 4) Empress replaces Queen. 5) Leo replaces Queen. 6) Tigers replace Bishops. 7) Sprinters replace Bishops. 8) Vaos replace Bishops. 9) Princesses replace Rooks. 10) Cannons replace Rooks. 11) Men replace Knights. 12) Zebras replace Knights. 13) Archers replace Knights. 14) Stars replace Knights. 15) Grasshoppers replace Knights.
The difference between this and the method for General Extended Random Variant Chess, which uses the same set of substitutions, is now that at most one of the possible four substitutions is made, while before a substitute for the Queen, one for the Bishops, one for the Rooks, and one for the Knights were all chosen independently. In this way, the basic array of conventional Chess pieces, instead of being replaced by something chosen completely at random is left largely intact, with only one kind of piece usually replaced by something else.
Both methods now continue as follows:
Then, one of the 45 variations for the unallotted two positions on each side of the board is chosen. The variation may need to be modified, depending on the replacements chosen for the Queen, the Bishops, or the Knights, as follows:
The first method provides for 16,200 possible opening arrays, all of which largely retain the symmetry and balance of forces of the regular game of Chess. The second method provides only 675 variations.
The first method of producing a random chess variant all but ensures that the ordinary chessmen, other than the King and the Pawns, will not be present. As this is not necessarily desirable, even if more than 45 possibilities are felt to be needed, the second method, which has the advantage that most of the conventional chessmen will still be present was developed. With 675 possible opening arrays, it should still provide sufficient variety to preclude an excessive reliance upon book openings.
Also note that if the Rooks are replaced by Cannons, castling may still take place, with the Cannons functioning as the Rooks, but if the Rooks are replaced by Princesses, there is no castling.
Only one combination of substitutions is chosen, and it applies to both players, just as the variation chosen from among those in the list of 45 variations applies to both players.
Examination of the possibilities offered by the two forms of Extended Random Variant Chess has suggested a third form, based on Restricted Extended Random Variant Chess. In this form, choosing the variant has three steps.
The first step is to choose a base array, from three possibilities involving related pieces:
1) Rook, ?, ?, Knight, Bishop, Queen, King, Bishop, Knight, ?, ?, Rook 2) Rook, ?, ?, Archer, Sprinter, Queen, King, Sprinter, Archer, ?, ?, Rook 3) Cannon, ?, ?, Knight, Vao, Leo, King, Vao, Knight, ?, ?, Cannon
The next step is to choose a substitution at random in the fashion of Restricted Extended Random Variant Chess. If General Extended Random Variant Chess were used, one could use the rule that "leaving the Knight alone" may mean "replacing the Archer by a Knight", and "replacing the Rook by a Cannon" may mean "leaving the Cannon alone". However, then the base array would be irrelevant. Since it is the substitution rule of Restricted Extended Random Variant Chess that is used, the substitutions have to be modified the opposite way to work: if Archers are present, "Replace Knights by Archers" must change to "Replace Archers by Knights", if Vaos are present, "Replace Bishops by Vaos" must change to "Replace Vaos by Bishops", so that all the possibilities of changing one piece in the base array selected remain available.
The third step is to choose one of the 45 variants for the positions noted by question marks.
Finally, as with Restricted Extended Random Variant Chess, since the Rhinoceros, Griffin, Tiger, Man, and Zebra are present in both the 45 variants and in the piece substitutions, duplication is to be dealt with by having the substitution take precedence, and modifying the variant chosen as follows:
This version, Systematic Random Variant Chess, allows the most interesting possibilities reachable by the General Extended version to be available, but retains the advantage of the Restricted Extended version of a less haphazard layout. It provides 1,935 possible opening layouts. (The number would be 2,025, except for two duplicate cases; as the second base array differs from the first base array in only two pieces, the combination with a Bishop and an Archer, or a Sprinter and a Knight, can be obtained with either array, and a different substitution in each case.)
Note that if it is considered a problem that some reachable arrangements are more probable than others, this can be solved as follows: consider the arrangements where an Archer or a Sprinter are substituted in from base array 1 as the original, and those where a Knight or a Bishop are substituted in from base array 2 as the duplicate, and make the duplicate arrangements unique by making the additional substitution of a Griffin for the Queen in that case.
In addition to the conventional promotion rule, that Pawns only promote to pieces found in the initial array for the particular game being played, two alternative promotion rules are advanced as possible options:
Pawns could be allowed to promote only to pieces which, while part of the pool of possible pieces from which a variant could be constructed, were not part of the initial array, subject also to the further restriction that only pieces of types not previously promoted to may be used.
This rule has two results: like promotion to captured pieces, it conserves physical chess pieces, and it further increases the variety of pieces potentially on the board. (Incidentally, note that neither the Bat, nor the Nightrider, two especially "troublesome" pieces, are included in the pool of those used for this variation.)
Alternatively, pawns could be, regardless of the specific variant in use, allowed only to promote to pieces found in the 'base' version of the array: Queen, Rook, Bishop, Knight, Camel, and Giraffe.
This would reduce the confusion that the large variety of possible initial arrays could potentially cause for promotion.
The Grasshopper, originally invented by T. R. Dawson, is one of the most popular Fairy pieces used in problems. I have given names to the Archer, Sprinter, and Star, but these are all such trivial combined pieces that they are unlikely to be original. The other pieces introduced on this page are well-established pieces used in Fairy Chess problems.
In surveying the many enlarged forms of Chess that have been proposed through the ages, from the earliest varieties of Decimal Chess and Great Chess down to modern innovations such as Ciccolini's Game and Capablanca's Chess, I have found that the type of array I have proposed as the basis for Random Variant Chess has been used very rarely, and another type of array has been much more common. This appears to be because it has been considered highly desirable to keep the ability to place the castled King in this secure corner arrangement:
| N | | | -+---+---+---| | P | P | P | -+---+---+---| | R | K | | --------------
Thus, instead of new pieces being added between the Knight and the Rook, as I thought to do so that the base array Rook, Giraffe, Camel; Knight, Bishop, King, Queen, Camel, Giraffe, Rook would concentrate the attacks of four pieces on each side on the squares in front of the Queen and the King, it seems to be the historical consensus of the chess world that new pieces ought to be added between the Queen and King and their flanking Bishops. Some versions instead added new pieces between the Bishops and Knights, so I suppose that is an alternate possibility that could be considered.
Interestingly enough, the one historical exception I have been able to find to this tendency, where the new pieces were placed in the place I was originally inclined to put them, between the Knights and the Rooks, was devised by Carrera in 1617. It is not only referred to in the book Chess Eccentricities by Major George Hope Verney, but it is also mentioned in the book introducing Chancellor Chess. It placed a Princess (that is, a piece with the moves of a Bishop and a Knight, but called a Centaur in this game) on the Queenside, and an Empress. (that is, a piece with the moves of a Rook and a Knight, called a Campione in this game) on the Kingside. Much later, in 1874, H. E. Bird devised a game with the same complement of pieces, but different names, where the two new pieces were between the two Bishops and the Queen and King (with the Empress called an Equerry, and placed next to the Queen, and the Princess called a Guard, and placed next to the King), and then, several years later, in 1921 or shortly thereafter, Capablanca placed the new pieces (the Princess called an Archbishop, and the Empress the Chancellor) between the Bishops and Knights on the two sides, this time with the Princess again on the Queenside. Surprisingly enough, all three games were designed for a board with 8 ranks and 10 files, rather than a 10 by 10 board; while this is more sensible, most enlarged Chess variants have tended to use a square board rather than following the example of Courier Chess. Capablanca, at least, did also consider the 10 by 10 board.
Given that the three basic moves in the modern game of Chess are those of the Rook, the Bishop, and the Knight, and that the Queen represents the combination of two of them, those of the Rook and Bishop, it should not be too surprising that the other combinations were thought of as obvious pieces to add to the layout.
Adding a Knight's move to the abilities of the Queen, giving rise to the Amazon, is another popular possibility; among the games which included this piece were the Emperor's Chess and the Sultan's Chess, both devised by L, Tressau in 1840.
Perhaps the most sensible arrangement would be to follow the location used for Bird's variant, but to put the Princess back on the Queenside to better balance the locations of the pieces by their power. That version probably has been thought up by someone historically as well.
One of the things I tried to do with Random Variant Chess was to avoid changing the power of the pieces in the array. Thus, the Empress, a Rook and Knight combined, was used as a replacement for the Queen, and not as one of the possible added pieces, and the Princess, a Bishop and Knight combined, or a Pao, the Cannon from Chinese Chess, could replace the Rook.
Yet, the Griffin, a very powerful piece indeed, is allowed as an added piece. So the goal of limiting the change in power of the pieces, while allowed to limit the number of variations, was not consistently met.
Thus, another factor incorporated in this revision of the game is to allow an increased variety in the piece substitutions and added pieces, and to use the Shatranj pieces as another alternative base array.
The diagram below shows the various forms of the basic layout that are intended to be provided in this form of the game:
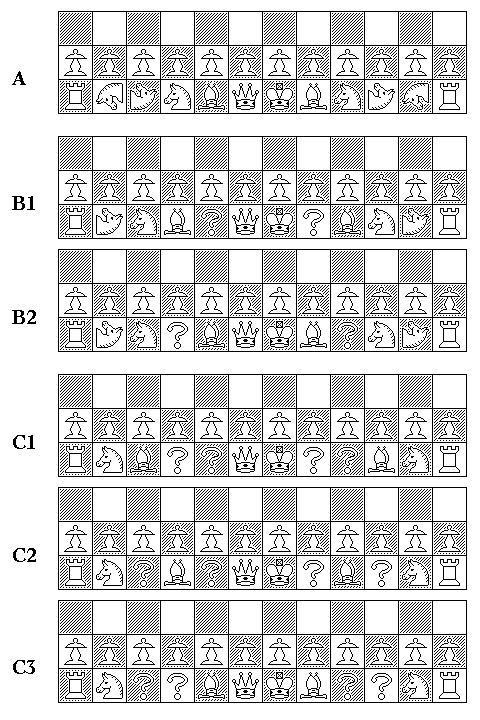
If both the Camel and the Giraffe are added to the complement of chess pieces, arrangement A is used. If only the Camel is added, either arrangement B1 or B2 is used. But if neither the Camel nor the Giraffe are added, then the Knight is kept next to the Rook, so as to preserve the castled position shown above, and either arrangement C1, C2, or C3 is used.
Some additional pieces, beyond those defined for Leaping Bat Chess on the previous page, and the additional ones defined above, will be provided here. The Counsellor combines the moves of the Man (or the King) and the Knight, and the Duke can move as a Rook or Bishop, but only one or two spaces, and the Count can move as a Rook, but only three spaces.
As a two-space move by the Duke is not a jump, this is not the Squire from RennChess, also used as the Mammoth or Mastodon by Mats Winther. It should be noted that RennChess, or Renniassance Chess, by Eric V. Greenwood, also has a piece called the Duke with a different move. The piece used here was called the Duke in Greater Chess, a game from 1942 invented by W. Day.
The Squirrel, on the other hand, combines the Dabbaba, the Alfil, and the Knight, and does jump to a square two steps away from it.
Thus, the added pieces are now chosen from this list:
With arrangement A
1) (Giraffe, Camel); (Camel, Giraffe)
With arrangements B1 and B2:
2, 3) (Camel), Fers; Fers, (Camel)
4, 5) (Camel), Wazir; Wazir, (Camel)
6, 7) (Camel), Man; Man, (Camel)
8, 9) (Camel), Alfil; Alfil, (Camel)
10, 11) (Camel), Dabbaba; Dabbaba, (Camel)
12, 13) (Camel), Man; Counsellor, (Camel)
14, 15) (Camel), Squirrel; Squirrel, (Camel)
16, 17) (Camel), Duke; Squirrel, (Camel)
18, 19) (Camel), Duke; Duke, (Camel)
20, 21) (Camel), Duke; Counsellor, (Camel)
22, 23) (Camel), Count; Count, (Camel)
24, 25) (Camel), Count; Counsellor, (Camel)
26, 27) (Camel), Count; Duke, (Camel)
28, 29) (Camel), Walker; Walker, (Camel)
30, 31) (Camel), Tiger; Tiger, (Camel)
32, 33) (Camel), Cannon; Cannon, (Camel)
33, 34) (Camel), Princess; Empress, (Camel)
35, 36) (Camel), Rhinoceros; Griffin, (Camel)
With arrangements C1, C2 and C3:
?L: Dabbaba Cannon Rhinoceros Zebra Princess
?R: Dabbaba Cannon Griffin Zebra Empress
?L, Fers; Fers, ?R 37, 38, 39 87, 88, 89 134. 135. 136 179, 180, 181 233, 234, 235
?L, Wazir; Wazir, ?R 40, 41, 42 90, 91, 92 137, 138, 139 182, 183, 184 236, 237, 238
?L, Man; Man, ?R 43, 44, 45 93, 94, 95 140, 141, 142 185, 186, 187 239, 240, 241
?L, Alfil; Alfil, ?R 46, 47, 48 96, 97, 98 143, 144, 145 188, 189, 190 242, 243, 244
?L, Dabbaba; Dabbaba, ?R 191, 192, 193
?L, Man; Counsellor, ?R 49, 50, 51 99, 100, 101 146, 147, 148 194, 195, 196 245, 246, 247
?L, Squirrel; Squirrel, ?R 51, 52, 53 101, 102, 103 149, 150, 151 197, 198, 199 248, 249, 250
?L, Duke; Squirrel, ?R 54, 55, 56 104, 105, 106 152, 153, 154 200, 201, 202 251, 252, 253
?L, Duke; Duke, ?R 57, 58, 59 107, 108, 109 155, 156, 157 203, 204, 205 254, 255, 256
?L, Duke; Counsellor, ?R 60, 61, 62 110, 111, 112 158, 159, 160 206, 207, 208 257, 258, 259
?L, Count; Count, ?R 63, 64, 65 113, 114, 115 161, 162, 163 209, 210, 211 260, 261, 262
?L, Count; Counsellor, ?R 66, 67, 68 116, 117, 118 164, 165, 166 212, 213, 214 263, 264, 265
?L, Count; Duke, ?R 69, 70, 71 119, 120, 121 167, 168, 169 215, 216, 217 266, 267, 268
?L, Walker; Walker, ?R 72, 73, 74 122, 123, 124 170, 171, 172 218, 219, 220 269, 270, 271
?L, Tiger; Tiger, ?R 75, 76, 77 125, 126, 127 173, 174, 175 221, 222, 223 272, 273, 274
?L, Cannon; Cannon, ?R 78, 79, 80 224, 225, 226
?L, Princess; Empress, ?R 81, 82, 83 128, 129, 130 176, 177, 178 227, 228, 229
?L, Rhinoceros; Griffin, ?R 84, 85, 86 131, 132, 133 230, 231, 232
Once an arrangement of the regular pieces and the added pieces is chosen from the 274 possibilities, the next step is to choose a base array and piece substitutions.
There are four possible base arrays. The first one has the forms as shown in the diagram above:
A) Rook, Giraffe, Camel, Knight, Bishop, Queen, King, Bishop, Knight, Camel, Giraffe, Rook B1) Rook, Camel, Knight, Bishop, ?, Queen, King, ?, Bishop, Knight, Camel, Rook B2) Rook, Camel, Knight, ?, Bishop, Queen, King, Bishop, ?, Knight, Camel, Rook C1) Rook, Knight, Bishop, ?, ?, Queen, King, ?, ?, Bishop, Knight, Rook C2) Rook, Knight, ?, Bishop, ?, Queen, King, ?, Bishop, ?, Knight, Rook C3) Rook, Knight, ?, ?, Bishop, Queen, King, Bishop, ?, ?, Knight, Rook
and the correspondence between the various base arrays is:
1 2 3 4 Rook Rook Cannon Rook Knight Knight Knight Archer Bishop Alfil Vao Sprinter Queen Fers Leo Queen
Either one base array, followed by one piece substitution, can be chosen, for Progressive Systematic Random Variant Chess, or the step of choosing a base array can be ignored, and a piece substitution for every piece can be chosen, giving Progressive Extended Random Variant Chess. It might also be desired to use just one piece substitution, but also to use either just one of the possible base arrays, or two or three of them selected to taste.
1
------------------------------
1/*) No substitutions.
*/1) No substitution for the Queen.
2/2) Fers replaces Queen.
3/3) Griffin replaces Queen.
4/4) Rhinoceros replaces Queen.
5/5) Nightrider replaces Queen.
6/6) Empress replaces Queen.
7/7) Leo replaces Queen.
8/*) Princess replaces Queen.
*/1) No substitution for Bishops.
9/2) Tigers replace Bishops.
10/3) Sprinters replace Bishops.
11/4) Vaos replace Bishops.
12/5) Alfils replace Bishops.
*/1) No substitution for Rooks.
13/2) Princesses replace Rooks.
14/3) Cannons replace Rooks.
*/1) No substitution for Knights.
15/2) Men replace Knights.
16/3) Zebras replace Knights.
17/4) Archers replace Knights.
18/5) Stars replace Knights.
19/6) Grasshoppers replace Knights.
2 3 4
------------------------------ ------------------------------ ------------------------------
1) No substitutions. No substitutions. No substitutions.
2) Queen replaces Fers. Fers replaces Leo. Fers replaces Queen.
3) Griffin replaces Fers. Griffin replaces Leo. Griffin replaces Queen.
4) Rhinoceros replaces Fers. Rhinoceros replaces Leo. Rhinoceros replaces Queen.
5) Nightrider replaces Fers. Nightrider replaces Leo. Nightrider replaces Queen.
6) Empress replaces Fers. Empress replaces Leo. Empress replaces Queen.
7) Leo replaces Fers. Queen replaces Leo. Leo replaces Queen.
8) Princess replaces Fers. Princess replaces Leo. Princess replaces Queen.
9) Tigers replace Alfils. Tigers replace Vaos. Tigers replace Sprinters.
10) Sprinters replace Alfils. Sprinters replace Vaos. Bishops replace Sprinters.
11) Vaos replace Alfils. Bishops replace Vaos. Vaos replace Sprinters.
12) Bishops replace Alfils. Alfils replace Vaos. Alfils replace Sprinters.
13) Princesses replace Rooks. Princesses replace Cannons. Princesses replace Rooks.
14) Cannons replace Rooks. Rooks replace Cannons. Cannons replace Rooks.
15) Men replace Knights. Men replace Knights. Men replace Archers.
16) Zebras replace Knights. Zebras replace Knights. Zebras replace Archers.
17) Archers replace Knights. Archers replace Knights. Knights replace Archers.
18) Stars replace Knights. Stars replace Knights. Stars replace Archers.
19) Grasshoppers replace Knights. Grasshoppers replace Knights. Grasshoppers replace Archers.
Note that Princesses may only replace Rooks, and not the Queen, if substitutions are chosen for individual pieces.
Then the final step is to avoid excessive numbers of certain Fairy pieces due to their possible occurrence in both the piece substitution and in the variant (that is, the group of two or four added pieces) above:
The number of different variants provided by Progressive Systematic Random Variant Chess is 274 variants times 4 base arrays times 19 piece substitutions, giving 20,824 possibilities, and the number of different variants provided by Progressive Extended Random Variant Chess is 274 variants times 7*5*3*6 (or 630) piece substitutions, giving 172,620 possibilities.
It has occurred to me that there is another reasonable family of variants that could be added to the 274 basic possibilities above.
For the two additional forms of the base array shown below:

with which the correspondences with the four base arrays remain:
1 2 3 4 Rook Rook Cannon Rook Knight Knight Knight Archer Bishop Alfil Vao Sprinter Queen Fers Leo Queen
with arrangements D1 and D2, we add to the 274 possibilities above:
?L: Tiger Cannon Princess Empress Zebra
?R: Tiger Cannon Princess Princess Zebra
?L, Man; Cannon, ?R 275 276 359 360 407 408 443 444
?L, Man; Griffin, ?R 277 278 323 324 361 362 409 410 445 446
?L, Man; Rhinoceros, ?R 279 280 325 326 363 364 411 412 447 448
?L, Man; Empress, ?R 281 282 327 328 365 366 449 450
?L, Fers; Cannon, ?R 283 284 367 368 413 414 451 452
?L, Fers; Griffin, ?R 285 286 329 330 369 370 415 416 453 454
?L; Fers; Rhinoceros, ?R 287 288 331 332 371 372 417 418 455 456
?L; Fers; Empress, ?R 289 290 333 334 373 374 457 458
?L, Wazir; Cannon, ?R 291 292 375 376 419 420 459 460
?L, Wazir; Griffin, ?R 293 294 335 336 377 378 421 422 461 462
?L; Wazir; Rhinoceros, ?R 295 296 337 338 379 380 423 424 463 464
?L; Wazir; Empress, ?R 297 298 339 340 381 382 465 466
?L, Walker; Cannon, ?R 299 300 383 384 425 426 467 468
?L, Walker; Griffin, ?R 301 302 341 342 385 386 427 428 469 470
?L; Walker; Rhinoceros, ?R 303 304 343 344 387 388 429 430 471 472
?L; Walker; Empress, ?R 305 306 345 346 389 390 473 474
?L, Duke; Cannon, ?R 307 308 391 392 431 432 475 476
?L, Duke; Griffin, ?R 309 310 347 348 393 394 433 434 477 478
?L, Duke; Rhinoceros, ?R 311 312 349 350 395 396 435 436 479 480
?L, Duke; Empress, ?R 313 314 351 352 397 398 481 482
?L, Count; Cannon, ?R 315 316 399 400 437 438 483 484
?L, Count; Griffin, ?R 317 318 353 354 401 402 439 440 485 486
?L; Count; Rhinoceros, ?R 319 320 355 356 403 404 441 442 487 488
?L; Count; Empress, ?R 321 322 357 358 405 406 489 490
increasing the number of starting arrays, before piece substitutions, from 274 to 490, and thus increasing the total number of combinations from 20,824 to 37,420 for Progressive Systematic Random Variant Chess. and from 172,620 to 308,700 for Progressive Extended Random Variant Chess.
Of course, normally, people playing the game would simply improvise equipment for it, should this game become popular, there would arise a demand for sets for the game. How could a set for a game like this be made without requiring an inordinate number of pieces, of wildly varied shapes, impossible to memorize?
The obvious improvised solution for a game like this would be to use multiple chess sets different in appearance or size. This suggests to me that a set specifically designed for this game could consist of the following, for each of White and Black:
This kind of piece would provide both an inexpensive indication of the exact type of the piece, and a differentiation of form comparable to what is normally expected from Chess pieces. For example, the shape could be that of a chessman on a square pedestal, with the pedestal being surrounded on its four corners by L-shaped posts a small distance from the pedestal to hold the piece's label.
But the problem may be that this is simply too complicated.
Perhaps the goal should be to have as little change from normal Chess as possible while still allowing a fair amount of variation.
How about this, then:
1) R ? N B Q K B N ? R 2) R N ? B Q K B ? N R 3) R N B ? Q K ? B N R
on a 10 by 8 chessboard, with six possibilities for replacing the Queen:
1) Queen (R+B) 2) Princess (B+N) 3) Empress (R+N) 4) Amazon (R+B+N) 5) Griffin 6) Leo
and the extra two pieces could be drawn from a fairly short list of alternatives:
1) Camel, Camel 2) Squirrel, Squirrel 3) Duke, Squirrel 4) Princess, Empress 5) Cannon, Cannon 6) Tiger, Tiger 7) Man, Counsellor 8) Duke, Duke 9) Duke, Counsellor 10) Count, Count 11) Count, Counsellor 12) Count, Duke
Then, the variation to be played could be chosen by rolling three dice of different colors, giving 216 possibilities. That might be as much variation as people would want, and as much as would be needed to achieve a game with more variety.
When the Princess and Empress are chosen as the additional two pieces, and either the Princess or the Empress is chosen to replace the Queen, instead two Cannons are used as the additional pieces,
If one keeps moving downwards, from a 12 by 8 board to a 10 by 8 board, the next step is the original 8 by 8 board.
Fischerrandom, sometimes also termed Chess 960, was an attempt to limit the amount of change to Chess caused by arranging the pieces randomly on the back rank. As noted, I've tried to avoid messy arrangements of pieces, and yet have a large number of possibilities, by adding extra pieces so that a much more restricted set of arrangements, mostly consisting of choosing pieces to add, would still lead to many possibilities.
If one were more restrictive than Fischerrandom, and insisted that the two Rooks and the King remained on their original squares, so that Castling would be completely unaffected, as well as insisting the Bishops be on squares of opposite color, the number of possible combinations would not be enough to make the game very random; if we added the restriction that one Bishop and one Knight had to be on each side of the King, there would be only six combinations:
R N B Q K B N R R B N Q K N B R R Q B N K B N R R Q N B K N B R R N Q B K N B R R B Q N K N B R
but if one used a four-player Chess board, then there would be thirty-six combinations:
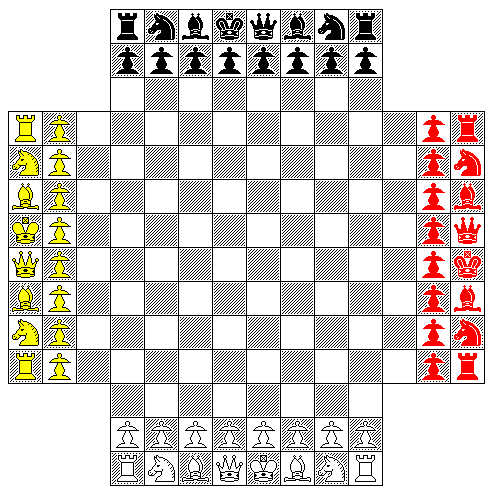
with one player using the white and yellow pieces, and the other the black and red pieces.
One could then go further; since the two groups of pieces each player controls are distinguished by color, they could be given other roles:
King -> Man Queen -> Empress Rook -> Princess Knight -> Giraffe Bishop -> Zebra
This way, each side has only one King. And, thus, the pieces could be left as they are for a game of Chess with extra pieces played on the four-player board, or the regular Chess pieces could be randomly placed in one of the six arrangements noted above - and the arrangement for the red and yellow pieces could be completely random, so the number of possible arrangements would be 5,020 times 6, or 30,120.