
The game of Leaping Bat Chess, outlined on the preceding page, avoids stereotyped openings by having, as it were, a pre-opening phase involving battles between the short-range pieces on the front rank. However, the large scale of that game changes its character considerably from that of regular Chess, despite my efforts to design the opening array in such a way to retain as many features of regular Chess as possible.
In Checkers, the first few moves of the two players are chosen randomly in an attempt to avoid stereotyped openings. Several proposals have been made to do this for Chess by shuffling the order in which the men are placed on the back rank.
It should be noted, though, that the two-move restriction was originally adopted for Checkers in 1863 as the result of a match of 40 games between James Wyllie and Robert Martins in which the same game was repeated from beginning to end 21 times. This became a three-move restriction some years later in the United States when the two-move restriction was felt to be inadequate; other countries in the English-speaking world switched to the three-move restriction much later.
While it is true that there is a burgeoning quantity of opening theory for Chess, the day when something on the order of that Wyllie-Martins match would take place is a very distant one indeed, if it will ever come. Chess is not on the verge of being "played out", therefore.
It is a credit to the love that Checkers players have for the game that they have been willing to put up with such things as the three-move restriction in order to save it. (Note that this applies to the version of Checkers played on an 8 by 8 board in the English-speaking world. The game of International Checkers, also known as Polish Checkers [it is called French Checkers in Poland; the name was given to it in Holland, where it actually originated, because it seemed strange and foreign compared to an earlier game played there on a 10 by 10 board but with only three rows of pieces on each side] has not yet faced a requirement for this type of move restriction.) Chess players, however, can quite legitimately claim that Chess is not broken, and therefore does not need to be fixed.
Innovations such as Capablanca Chess, Fischer Random Chess, or, most recently, Seirawan Chess, though, have been advocated on the basis that such factors as the level of opening theory mean that the standard game of Chess does face problems, even if they are milder than those which the game of Checkers has faced.
Very recently, an interesting variant of this form was developed by M. Winther, called Placement Chess. It avoids the need for randomly choosing one of 960 possible starting arrays with elaborate equipment.
Before play starts, the two players establish the arrangement of pieces as follows:
First, Black selects the initial position of the King. The King can retain its initial position, or be exchanged with the Queen's Bishop or either Knight. The position so selected applies to both player's arrays.
Then, White selects the initial position of the Queen. The Queen can retain its initial position, or be exchanged with the King's Bishop or either Knight.
Whatever the initial position of the King may be, the King may castle; the result of castling is that the King and Rook involved are placed at the same positions as would result from castling in normal Chess.
Because the problems are less serious, it follows that even if people are willing to address them by playing a game with different rules, they would be less willing to accept a drastic remedy. Thus, I have tried to devise something which achieves the same result as the three-move restriction does for Checkers, or as shuffling the array of pieces does for Chess, but which involves less disturbance of the feel of ordinary Chess.
My original goal was to address one complaint that people have about conventional Chess: that there is a great amount of opening knowledge to be studied and memorized in order to play the game well. Instead of randomizing the arrangement of the conventional pieces, as in Chess 960, or adding a few pieces with new moves - which, obviously, would only be a temporary solution, as a new static variant would develop its own body of opening knowledge - I propose to maintain a conventional symmetric array, but randomly choose which pieces to use in the game from a limited selection.
But there is another more serious complaint about conventional Chess: once Steinitz came along, and put Chess strategy on a sound, rational basis, thus establishing the Modern school of Chess, the game has become, at least, less attractive for spectators, as it now tends to end in a draw too often.
Elsewhere on this site, I have outlined my attempt to address this with Dynamic Scoring, and a version of that is incorporated into this version of Chess explicitly, however, with significant changes after further re-thinking.
Given that a similar situation happened in the game of Go (or Weiqi) after Honinbo Shusaku, which led to the first player (Black, in that game) always winning by a few stones with sound defensive play on both sides, and it was corrected through the adoption of komidashi, requiring Black to win by a certain margin to claim victory, I sought to find a way to add something similar to Chess.
I have decided to present first a revised version of Random Variant Chess which, I hope, will be seen as simpler and more straightforward than the versions I have previously offered.
For the first thing, as with Chess 2016, the random variant to be used will be selected by the roll of three identical dice.
The basic layout will be:

and thus, each player's pieces will be in the array:
Rook, Giraffe, Camel, Knight, Bishop, Queen, King, Bishop, Knight, Camel, Giraffe, Rook
behind a row of twelve pawns.
This introduces two additional types of piece beyond those used in normal Chess, the Camel and the Giraffe.
The Camel is a 1-3 leaper. That is, it has up to eight possible moves, involving a displacement of three units in one orthogonal direction, and one unit in the other orthogonal direction. It is confined to one color of square, which makes it a weaker piece than either the Knight or the Bishop, since it is both confined to one color (like the Bishop) and a short-range piece (like the Knight).
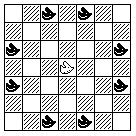
The Giraffe moves four squares in one orthogonal direction, and one square in a perpendicular orthogonal direction, ignoring intervening pieces. Thus, its move is similar to that of a Knight, except longer, and, like a Knight, it changes color with each move.
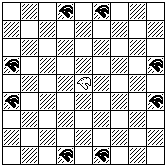
In the standard form of this game, Castling, whether to Kingside or Queenside, is a four-square move of the King, followed by a leap by the Rook over the King to the next square beyond. It will be noted below how this changes for some of the variants.
While this standard form of the game closely resembles the standard layout for Chess, and so it might be thought that it would lead to a similar game, it does have one problem.
In order to avoid making the game slower than normal Chess, a board with the normal eight ranks, although it is enlarged to twelve files, was chosen. But two pieces similar to the Knight, the Camel and the Giraffe, were added which had longer moves.
Although the Camel is weaker than either the Knight or the Giraffe, being confined to squares of one color, the length of its move is just right, and it is so situated, as to cause the whole opening of the game to revolve around it!
To discuss the matter, let us adapt algebraic Chess notation to this enlarged board as follows:

Although the use of the letters i and l to denote files might have the potential to cause confusion, as I am not setting an official standard here, I did not feel at liberty to choose a special arrangement of the alphabet for this; as well, the relative position of letters and digits being fixed in algebraic Chess notation, there seemed no real cause for concern.
Now then: if the Camel on j1 is moved to either i4 or k4 on its first move, then on its second move it can capture the Pawn on i7, giving check.
If the other player has made conventional moves, such as advancing the Queen's Pawn to f6 or the King's Pawn to g6, it won't be mate, but the King will have had to move, thus forfeiting the ability to Castle.
And, of course, Black has the same threat, and a similar threat to the Queen exists on the Queenside. This might encourage an initial series of moves such as:
1. j4 j5 2. c4 c5
to forestall such a threat, but that doesn't quite work either:
1. j4 GxP
as the Giraffe on k8 can capture a Pawn placed on j4 in order to keep the Camel on j8 away from the dangerous squares i5 and k5. If one prepares the way by first advancing the Pawn on i2 to i3 to defend the j4 square, one is too late to prevent the Camel from going to one of those squares on the opponent's first move!
There is, though, a conventional first move that is a valid defense against this trap, so the game is not unplayable, although this will lead to a more stereotyped opening: if the Knight on i1 leaps to h3, it then defends the critical j2 square against the intrusion of the opponent's Camel. So, presumably, games might begin like this:
1. Nh3 Nh6 2. Ne3 Ne6 3. g4 ...
rather than advancing the Pawn to g4 on the first move. But since the Knight attacks the j2 square, rather than the i5 and k5 squares, that move can be played on the second move, and thus 1. g4 or 1. f4 are still viable openings.
The roll of three dice is translated into the particular variant to be played as follows:
If all three numbers on the dice are identical, a variant is chosen from the list below:
1-1-1 The standard form of the game, without changes. 2-2-2 The Queen becomes an Empress, the Rooks become Princesses. 3-3-3 The Queen becomes an Amazon. 4-4-4 The Queen becomes a Fers, the Bishops become Elephants. 5-5-5 The Queen becomes a Griffin. 6-6-6 The Queen becomes a Rhinoceros.
The Empress has the move of the Rook and the Knight.
The Princess has the move of the Bishop and the Knight.
The Fers moves one square diagonally.
The Elephant moves one square diagonally or one square forwards.
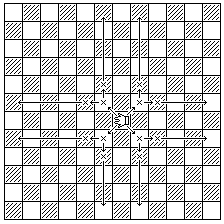
The Griffin is a powerful piece, almost equal to the Queen, based on similarly-named pieces occuring in some ancient Great Chess variants. Its move is as follows: it takes first one step diagonally, and then it takes a second orthogonal step as required to move a Knight's move from its original position. The third and subsequent steps of its move are in the same direction as its second step.
When moving, it must make a move of three or more steps; but it may capture with a move of one or two steps. (It may also capture with its normal, longer move.) Thus, although it can't make normal moves that the Bishop or Knight can make, it cannot be blocked by an opposing piece it cannot capture, nor does it leap over intervening pieces.
Thus, the following diagram illustrates its move:
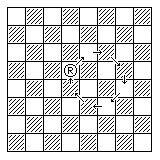
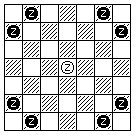
The Rhinoceros makes a move of from one to seven steps.
The first step may be orthogonal or diagonal.
The second step is a move of the opposite type continuing in an outward direction, leading to a square a Knight's move away from the original position.
Subsequent steps continue the alternation between diagonal and orthogonal moves, and each such step involves a 45 degree course change from the preceding step, with each such course change being to the same side.
Thus, the Rhinoceros moves around in circles, as the following two diagrams attempt to illustrate:
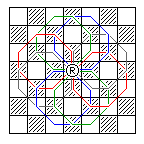
The Amazon has the moves of the Queen and the Knight.
When the Rooks are replaced by Princesses, Castling is not available.
If two of the numbers on the dice are identical, the variant to play is chosen as follows:
If the number that appears once is smaller than the number in the pair, then the number that appears once indicates which piece replaces the Camel, and the paired number indicates which piece replaces the Giraffe, as shown in the following table:
1 : Fers 2, 2-2: Wazirs 3, 3-3: Men 4, 4-4: Zebras 5, 5-5: Tigers 6-6: Cannons
The Tiger moves, without capturing, as a Bishop, and captures as a Knight.
The Cannon, as the corresponding piece from Chinese Chess, moves as a Rook, and captures along Rook lines, but to capture, must leap over one piece of either color. Both the portion of the move before the piece leaped over (the screen) and after that piece may be one or more squares in length.
The Man moves to any adjacent square, orthogonally or diagonally, like the King, but it has none of the special attributes of the King.
The Wazir moves one square orthogonally.
The Zebra jumps, ignoring intervening pieces, from its initial square, to a square that is two squares away in one orthogonal direction, and three squares away in the other orthogonal direction. Thus, its move is one diagonal step further out than a Knight's move.
Like the Knight, the color of the space on which it is sitting changes with each move.
If the paired number is smaller than the number that is the singlet, then the paired number indicates which piece replaces the Camel, and the number that appears only once indicates which piece replaces the Giraffe, according to the following table:
1-1: Walkers 2, 2-2: Elephants 3, 3-3: Stars 4, 4-4: Tigers 5, 5-5: Catapults 6 : Princess replaces Queen's Giraffe, Empress replaces King's Giraffe
The Walker moves without capturing one space orthogonally in any direction, like a Wazir, and captures one space diagonally in any direction, like a Fers. Thus, it is like a Pawn that can move in any direction.
The Star moves either one space orthogonally or two spaces orthogonally. When moving diagonally, it ignores any piece on the intervening square.
The Catapult is similar to the Cannon in Korean Chess; it must leap over another piece of either color to move as well as to capture. It may then move as a rook to any square beyond the piece over which it has leapt, as long as it does not leap over any additional pieces. However, unlike the Cannon in Korean Chess, it may leap over and it may capture another Cannon without restriction.
Note that only the Tiger appears in both sequences of possible replacements.
When all three numbers on the dice are different, each number indicates the following action is to take place:
1 Add Men 2 Add Elephants 3 Replace the Rooks by Cannons. 4 Replace the Bishops by Tigers. 5 Replace the Knights by Horses, and (if present) the Camels by Horse-Camels and the Giraffes by Horse-Giraffes. 6 Replace the Queen by a Griffin.
When one number indicating that a piece is to be added to the board is rolled, two of that piece are added to the board between the Queen and the King, and the Giraffes are removed from the board, with the Camels, Knights, Queen and King all being displaced outwards from the center. In that case, Castling becomes a three-square move of the King, followed by the Rook leaping over the King to the next square beyond.
When both of the numbers indicating that a piece is to be added to the board are rolled, both the Giraffes and the Camels are removed from the board, and the pieces added between the Queen and King are in the order:
Man, Elephant, Elephant, Man
In this case, Castling becomes a two-square move of the King, followed by the Rook leaping over the King to the next square beyond, as in standard Chess.
Castling may still take place if the Rooks are replaced by Cannons, with the Cannon playing the same part in the move as the Rook it replaced would have.
The Horse makes a move involving the same displacement as the move of a Knight, but the move explicitly consists of a move of one square orthogonally followed by one outwards diagonal move, and thus the Horse may be blocked by a piece on the intermediate square.
The Horse-Camel, similarly, moves two squares orthogonally followed by one square in an outward diagonal direction, and thus, unlike the Camel, may be blocked.
The Horse-Giraffe again, moves three squares orthogonally, followed by one square in an outward diagonal direction, and may be blocked.
Keeping the equipment required to select a variant simple, three identical dice, and avoiding the need for extended tables to describe the variant to be selected beyond those given above, the following scheme is proposed for selecting a variant by permitting a second roll of the three dice:
If the first roll consisted of three numbers which were all the same, the dice are not rolled a second time, the variant indicated is taken as is.
If the first roll consisted of a single number and a pair of numbers, the second roll modifies the variant indicated by the first roll as follows:
If the second roll consists of three identical numbers, as these rolls modify pieces other than the Camels and Giraffes, the modifications of the layout which they indicate are to be made in addition to that indicated by the first roll. A roll of 1-1-1, of course, indicates no modifications.
If the second roll also consists of a single number, and a pair of identical numbers, then action is taken as follows:
If in both rolls, the single number is smaller than the paired number, or in both rolls, the paired number is smaller than the single number, the second roll is ignored, unless the single number or the paired number is the same in the second roll as in the first roll. In that case, only the piece indicated by the matching number is added to the layout, and the numbers which do not correspond are ignored in both rolls, but whether that piece is specified to replace the Camels or the Giraffes, it will always replace the Giraffes.
Note that if the second roll is identical to the first roll, the effect would be the same, as if the second roll were ignored, if an attempt were made to apply the second rule to that case.
But if the two rolls are of opposite kinds in this respect, the first roll is used to indicate which piece replaces the Giraffes, and the second roll is used to indicate which piece replaces the Camels.
If the second roll consists of three numbers which are all different, then the numbers 1 and 2, if they appear in that roll, cause no action to be taken, but the other four numbers, 3, 4, 5, and 6, indicate actions to be taken to further modify the layout indicated by the first roll.
In addition, if the number 5 appears in the second roll, and the layout indicated by the first roll contains one or more Zebras, the Zebras are replaced by Horse-Zebras.
The Horse-Zebra moves one space orthogonally, followed by two spaces diagonally outward, and may be blocked by intervening pieces of either color. This is the move of the Elephant in Korean Chess.
If the first roll consisted of three different numbers, then the layout indicated by that roll is modified by the second roll according to the following rules:
If all three numbers in the second roll are different, then only those modifications in the layout which are indicated by numbers that appear in both the first roll and the second roll are made.
The remaining rules apply to the case where all three numbers are the same as well as to the case where the roll consists of a pair of numbers and another distinct number:
If the first roll includes both a 1 and a 2, and the second roll indicates that the Camels or Giraffes are to be replaced, that modification is to be ignored. If it includes only one of 1 or 2, and the second roll indicates that the Giraffes are to be replaced, that modification is to be ignored. As well, if it contained a 1 but not a 2, an indication in the second roll that the Camels are to be replaced by Men is to be ignored, and if it contained a 2 but not a 1, an indication in the second roll that the Camels are to be replaced by Elephants is to be ignored.
If the first roll contained a 3, 4, or 6, then anything in the second roll that indicates another replacement for the piece these numbers have caused to be replaced is to be ignored.
The inclusion of a 5 in the first roll does not, of itself, cause anything in the second roll to be ignored, but if the second roll introduces a Zebra to the board, that Zebra becomes a Horse-Zebra.
Examples:
2-2-2 Pr Gi Cam N B Em K B N Cam Gi Pr 2-4-4 2-2-2 Pr Ze Wa N B Em K B N Wa Ze Pr 2-4-4 2-3-3 R Wa Cam N B Q K B N Cam Wa R 2-4-4 3-4-4 R Ze Cam N B Q K B N Cam Ze R 2-4-4 5-2-2 R Ze El N B Q K B N El Ze R 5-2-2 2-4-4 R Ctp Wa N B Q K B N Wa Ctp R 5-2-2 1-3-5 Can Ctp El Hr B Q K B Hr El Ctp Can 1-3-5 2-4-5 R hGi hCm Hr B Q K B Hr hCm hCi R 1-3-5 2-4-6 R Gi Cam N B Q K B N Cam Gi R 1-4-5 1-4-6 R Cam N Ti Q Man Man K Ti N Cam R 1-4-5 3-3-3 R hCa Hr Ti Am Man Man K Ti Hr hCa R 1-4-5 2-4-4 R Wa Hr Ti Q Man Man K Ti Hr Wa R 1-4-5 4-6-6 R hZe Hr Ti Q Man Man K Ti Hr hZe R 1-4-5 5-6-6 R Ti Hr Ti Q Man Man K Ti Hr Ti R
In this version of the game, checkmate is worth 100 game points.
If one player forces stalemate, the points are split with 60 game points going to the player that forces stalemate, and 40 game points to the other player. In this way, a stalemate is worth only 1/5 as much as a checkmate, and thus players are still strongly encouraged to avoid letting a possible checkmate slip away to become a mere stalemate, but when only a stalemate is genuinely possible, something can still be put on the scoreboard.
After initially placing the rules for this latest variant on my web site, I realized that since Stalemate is nearly as difficult to achieve as Checkmate, if in addition to meaningfully addressing the issue of Chess becoming too drawish since the Modern school of chess play was adopted, I also wished to retain the feel of Chess in the important respect of ensuring that the emphasis is on winning the game through an attack on the King, and not on gaining material, I would have to retain perpetual check as a winning condition, instead of having only Material Superiority as a lesser win condition than Stalemate. However, precisely because Perpetual Check is much easier to achieve than Stalemate, it is possible that White's advantage of the first move is sufficient, or close to sufficient, to force Perpetual Check. In the former case, the remedy I plan to attempt will not avail me, but in the latter case, by going back to the original scheme of Dynamic Scoring by having different values for win conditions for the two sides, instead of only having the closer equivalent to komidashi in evaluating material superiority, following Korean Chess, it should be possible to promote aggressive play by both sides. |
When a game ends due to Perpetual Check, that is, when one side is capable of placing the opponent's King in check on every move with no chance of escape, the checking player wins. If White wins in this fashion, White receives 52 game points, and Black receives 48 game points. But if Black wins in this fashion, Black receives 55 game points, and White receives 45 game points.
When a game ends because nothing remains to be gained for either player, a victory is also possible due to material superiority. In this case, the points are split with 51 game points going to the winning player, and 49 game points going to the losing player. Thus, a stalemate is worth ten times, and a checkmate is worth fifty times, as much as a victory by material superiority, which can be viewed as nearly a draw.
The amount of material on each side is determined by giving the following values in material points (not to be confused with the game points the distribution of which was just described immediately above) to each of the possible types of piece used:
110 Amazon 95 Griffin 90 Queen 88 Empress 81 Rhinoceros 50 Rook 48 Princess 40 Cannon 35 Catapult 32 Bishop 31 Tiger 30 Knight 29 Giraffe, Horse, Star 28 Horse-Giraffe, Zebra 27 Horse-Zebra 26 Man 20 Camel 19 Horse-Camel 18 Wazir 17 Walker 15 Fers 10 Pawn
In addition, 4 1/2 material points are added to the value of the material held by the player with the Black pieces, to compensate for the White advantage of the first move, following the practice used with Korean Chess. This number of material points, as with komidashi in Go, may be changed as experience in play accumulates.
A draw, however, is still possible. After 4 1/2 material points are added to the value of the material held by Black, it is necessary for one player to be ahead by 6 or more material points to score a victory by Material Superiority; otherwise, the game is a draw, with the points split 50-50.
A series of wins by the White player or the Black player, after all, is just as indecisive as a series of draws, and so having a minimum threshold for a win by Material Superiority avoids pointless additions and subtractions... as well as providing two points, rather than one, at which a player may gain a genuine advantage on the scoreboard.
The four victory conditions, Checkmate, Stalemate, Perpetual Check, and Material Superiority, are in the successive ratios of 5:5:2 for White, and of 5:2:5 for Black. That is, Checkmate is worth five times as much as Stalemate for both players, and Stalemate is worth ten times as much as Material Superiority for both players, but Stalemate is worth five times as much as Perpetual Check, and Perpetual Check is worth twice as much as Material Superiority for White, whereas Stalemate is worth twice as much as Perpetual Check, and Perpetual Check is worth five times as much as Material Superiority, for Black.
It is hoped that this method of scoring, which is also applicable to the normal game of Chess on the 8x8 board, is simple enough that it can be put to use, and its merits appreciated.
In both match and tournament play, when the dice are rolled to determine a variant to be played, this variant is in effect for two games or two rounds of play.
To alternate which player has White for the first game with a new variant, and to achieve a better balance between the degree to which each player has the advantage of the first move, in a match between two players, A and B, it will be randomly selected which of the two players has White for the first game, and then that player will have Black for the second and third games, White for the fourth and fifth games, and so on, alternating in pairs of games starting with an even-numbered game.
In tournament play, similarly, it will be attempted to have players change color only after odd-numbered games; and, furthermore, it is to be preferred that, when exceptions to this are required, that they take the form of some players also alternating colors after an even-numbered game rather than some players failing to change colors after an odd-numbered game.
After the first form of Random Variant Chess was described here, I realized that this form of the game fails to preserve one important element of Chess, the ability to place the King in a secure Castled position, because in many cases it will not be possible to leave a wall of Pawns in front of the King after the pieces that prevent Castling are moved out of the way.
So I have attempted to modify Random Variant Chess to address this concern. Two such modifications, attempted before the version shown on this page, are noted below, and the original version presented here is now provided on the third page: