Inspired by Anthony S. M. Dickins' book, A Guide to Fairy Chess, every now and then for quite some time I have tried to design alternate forms of Chess that would capture the many possibilities outlined in that book.
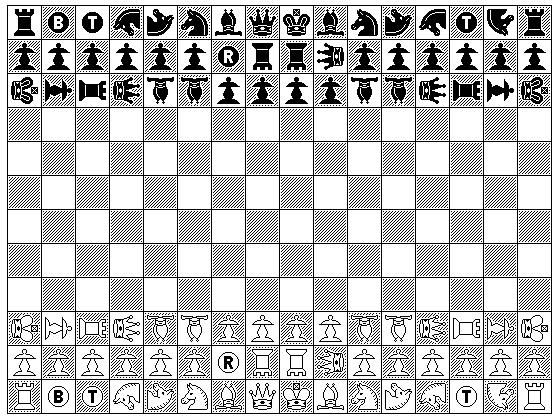
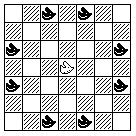
Here is the layout of the form I have currently settled upon:

Note that it is played on a board with 12 ranks and 16 files.
The pieces in the array are as follows:
Back rank (from White's left to right):
Rook
Bat
Tiger
Giraffe
Camel
Knight
Bishop
Queen
King
Bishop
Knight
Camel
Giraffe
Tiger
Nightrider
Rook
Second rank:
6 Pawns
Rhinoceros
2 Dabbabas
Griffin
6 Pawns
Third rank:
Man
Walker
Wazir
Fers
2 Alfils
4 Pawns
2 Alfils
Fers
Wazir
Walker
Man
For normal play, however, both the Bat and the Nightrider are to be replaced by Zebras, as the move of the Bat will tend, in general, to make play unduly difficult. The canonical version, with Bat and Nightrider, is primarily for use for problems. Alternatively, the Bat can be replaced by a second Nightrider. In any case, Pawns promote only to the pieces found on the initial array of the variant chosen.
Thus, the canonical form is "Leaping Bat Chess", the form with two Zebras is "Missing Bat Chess (Zebra)", and the form with a second Nightrider is "Missing Bat Chess (Nightrider)". Missing Bat Chess (Zebra) is the form recommened for actual play.
The rules are largely those of standard Chess, except that the 50-move rule is replaced by a 500-move rule, given the larger size of this variant, and in tournament or match play, a player who succeds in forcing stalemate is to recieve 3/5 of a point, while that player's opponent recieves only 2/5 of the point for the game.
Only the Bat and the Rhinoceros are pieces of my own invention; I have given new names to the Walker and the Tiger, but they are pieces of a fairly standard type, which have doubtless been used before. The Griffin, although a piece from an old Great Chess variant, has had its move slightly modified here as well. The other pieces are all well-known and established, and are in no way original.
The moves of these pieces are as follows:
The Rook moves as in standard Chess. The rules for castling on the enlarged board will be described in the paragraph concerning the King.
The Bat is a Root-65-Leaper. That is, near the center of a sufficiently large board, it will have sixteen possible moves; eight moves involving a displacement of 8 units in one orthogonal direction and 1 unit in the other, and eight moves involving a displacement of 7 units in one direction, and 4 units in the other.
- - - * * - - - - - * - - - * - - - - - - - - - - - - - - - - - - - * - - - - - - * - - - - - - - - - - - - - - - - - * - - - - - - - * - - - - B - - - - * - - - - - - - * - - - - - - - - - - - - - - - - - * - - - - - - * - - - - - - - - - - - - - - - - - - - * - - - * - - - - - * * - - -
Like the Knight, it changes color with each move.
The Bat at b1 in the initial array in the standard position can move to i5 as its first move. From that square, it threatens to capture either Black's Camel on e12, or Black's Giraffe on m12. Black can respond defensively by moving his Camel to either d9 or f9, as his Giraffe on m12 is defended by his Alfil on k10.
White's Bat can also move initially to either a9 or c9, but it is liable to immediate capture on those squares.
If White's Bat moves to f8 on its first move, it also threatens Black's (defended) Giraffe on m12.
As is clear from the foregoing, the long-range leap of the Bat requires careful attention.
As noted, the Bat can be called a Root-65-Leaper. Thus, its move was inspired by that of two existing pieces in Fairy Chess, the Fiveleaper and the Root-50-Leaper. The diagram below shows the distances of different types of move from a starting square:
and it can be seen from this diagram that the Fiveleaper has four orthogonal moves of five squares, plus eight moves with displacements (3,4), similar to an enlarged Knight's move; the Root-50-Leaper can be thought of as having the same move, but rotated by 45 degrees and enlarged by the square root of two, so that it has the same move, but on one color of square only (the Camel is similarly the analog of the Knight, and the Bishop the analog of the Rook, in this way), and thus it has four diagonal moves of five squares, and eight moves with displacements (1,7), again, similar to an enlarged Knight's move; and, finally, this new piece has eight moves with displacements (1,8), and another eight moves with displacements (4,7), thus making two different kinds of enlarged Knight's move.
The Tiger is a Bishop-mover/Knight-capturer. That is, it can move, but not capture, as a Bishop, and it can capture (and give check), but not move, as a Knight.
Since it is normally confined to one color, but changes colors when capturing, each time a Tiger captures, one switches between having two Tigers of opposite colors and having two Tigers of the same color, which creates an interesting strategic consideration.
The Giraffe is a 1-4 leaper. That is, it has up to eight possible moves, involving a displacement of four units in one orthogonal direction, and one unit in the other orthogonal direction. Like the Knight, whose move it resembles except for being more elongated, it changes color with each move.
- * * - - - - - - - - - - * - - - * - - G - - * - - - * - - - - - - - - - - * * -
The Camel is a 1-3 leaper. That is, it has up to eight possible moves, involving a displacement of three units in one orthogonal direction, and one unit in the other orthogonal direction. It is confined to one color of square, which makes it a weaker piece than either the Knight or the Bishop, since it is both confined to one color (like the Bishop) and a short-range piece (like the Knight).
- * - * - - - - - * - - - * - - C - - * - - - * - - - - - * - * -
The Knight moves as in standard Chess.
The Queen moves as in standard Chess.
The King moves as in standard Chess, but with two exceptions. When castling, whether to Kingside or Queenside, it moves six squares instead of two. Also, once per game, it may make a Knight's move. This move is compulsory when the King would either be checkmated or stalemated, even if, in the latter case, making this move would be to the player's disadvantage (i.e., because eventual later checkmate is inevitable).
The Nightrider moves one or more steps, where each step is a Knight move in the same direction. It can be blocked on any of the places it can move to in the same way as a Bishop or Rook.
The Pawn moves as in standard Chess, including having the ability to move two squares ahead on its first move, and being liable to en passant capture if it does so.
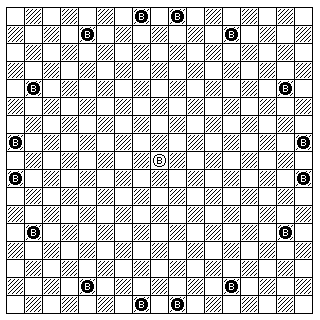
The Rhinoceros is an unusual rider, which goes around in circles. In this way, it can demonstrate the self unpin on a regular board.
The move of the Rhinoceros is as follows:
Its move is from one to eight steps. Its first step can be to any adjacent square, like the King's move. The second step must be diagonal, if the first step was orthogonal, or orthogonal, if the first step was diagonal, and must otherwise continue the direction of the first step as far as possible (that is, the second step must involve a course change of 45 degrees compared to the direction of the first step). On the second step, the Rhinoceros will always be a Knight's move away from its original position.
On its third and subsequent steps, it continues making the same angular course change from the preceding step as it made from its first step to its second step.
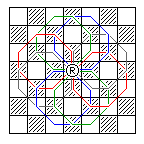
The diagram below shows one of the sixteen possible circular paths in which a Rhinoceros can move, and another possible path consists of taking the steps shown in the reverse order (a second color image attempts to show all possible paths):
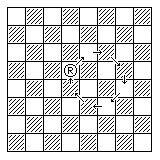
- - - - 1 2 - R - 3 7 - 4 - 6 5 -
Even when pinned against the King, the Rhinoceros can still move to another square, as long as the check is blocked at the end of the move. This is what is known as a self unpin. Also note that since it can move up to eight steps, when its path is suitably unobstructed, it can move around in a circle back to where it started from.
The idea of a piece that moves around in circles is not, I see, original with me. The Rose is a Fairy Chess piece not used in this game which achieves the same thing by making successive Knight moves in different directions, like this:
- - - - - - - - - - 1 - - - - - R - - 2 - - - - - - - - - - 7 - - 3 - - - - - - - - - - 6 - - 4 - - - - - 5 - - - - - - - - -
The Dabbaba moves exactly two squares orthogonally, ignoring intervening pieces.
The Griffin is a powerful piece, almost equal to the Queen, based on similarly-named pieces occuring in some ancient Great Chess variants. Its move is as follows: it takes first one step diagonally, and then it takes a second orthogonal step as required to move a Knight's move from its original position. The third and subsequent steps of its move are in the same direction as its second step.
When moving, it must make a move of three or more steps; but it may capture with a move of one or two steps. (It may also capture with its normal, longer move.) Thus, although it can't make normal moves that the Bishop or Knight can make, it cannot be blocked by an opposing piece it cannot capture, nor does it leap over intervening pieces.
Thus, the following diagram illustrates its move:
- * * - - - * - * - - x x - * * x x - x x * - - G - - * * x x - x x * - x x - - - * - * -
The Man moves one step either orthogonally or diagonally, like a King, but is just an ordinary piece.
The Walker is a Wazir-mover/Fers-capturer. That is, it moves, but does not capture, by taking one orthogonal step, and it captures, but does not move, by taking one diagonal step.
The Wazir moves one step in any orthogonal direction.
The Fers moves one step diagonally.
The Alfil moves exactly two squares diagonally, ignoring intervening pieces.
The Zebra, which is not part of the standard layout, but which normally replaces both the Bat and the Nightrider as shown therein, is a 2-3 leaper; that is, it has up to eight possible moves, involving a displacement of 3 units in one orthogonal direction, and a displacement of 2 units in the other orthogonal direction. Like the Knight, it changes color with each move.
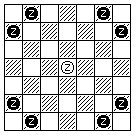
* - * * - - * - - - - - Z - - - - - * - - * * - *
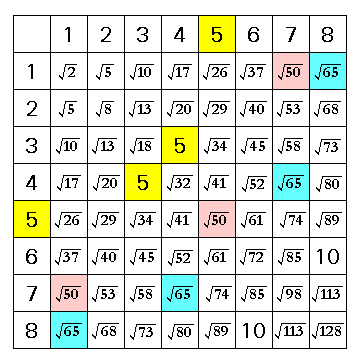
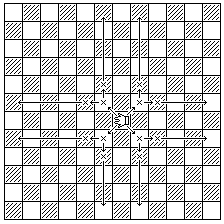
Note that it would take eight Alfils, or four Dabbabas, to reach every square on the board. With the pieces as situated in the initial array, every square on the board may either be reached by one of White's Alfils (if on an odd-numbered rank) or by one of White's Dabbabas (if on an even-numbered rank). Because the board has an even number of ranks, the squares reachable by one of White's Alfils are the squares reachable by one of Black's Dabbabbas, and vice versa. Chequering the board according to the color scheme shown in the following diagram:
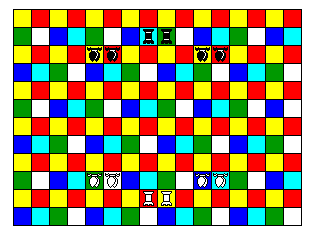
makes White's possible moves easily apparent; the yellow and red squares are the squares each of his two Dabbabas can reach, and the blue, green, white, and light blue-green squares are the squares each of his four Alfils can reach.
In practice, one would have to use eight colors to make the board equally usable by both players, or one could use a more complicated arrangement where each square had an area on it showing its color from White's viewpoint, and another showing its color from Black's viewpoint, as illustrated by the image below:

The complexity of the coloring scheme, and the number of different types of men on the board, however, has suggested to me that I might present a somewhat simpler version of this game which still has the same large board and the same number of pieces on each side, which I will call Complete Alfil Chess. (Of course, by so designating it, I am taking the very great risk that it will wind up being called Completely Awful Chess, at least on occasion.)
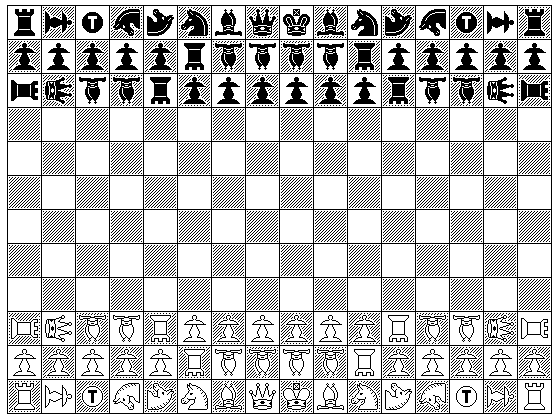
The rules are as above, but now the array consists of:
Back rank (from White's left to right):
Rook
Walker
Tiger
Giraffe
Camel
Knight
Bishop
Queen
King
Bishop
Knight
Camel
Giraffe
Tiger
Walker
Rook
Second rank:
5 Pawns
Dabbaba
4 Alfils
Dabbaba
5 Pawns
Third rank:
Wazir
Fers
2 Alfils
Dabbaba
6 Pawns
Dabbaba
2 Alfils
Fers
Wazir
This gives each side four Dabbabas and eight Alfils, and thus every square on the board can be reached by one of a player's Alfils and one of a player's Dabbabas. Thus, a single coloring scheme can work for both players.