The reason that hexagonal chess was invented is the same reason that most wargames are played on a hexagonal grid: since on a square grid, it is possible to move to four squares that are adjacent to each square, and in the same relation to it, while on a hexagonal grid, it is possible to move to six hexagons that are adjacent to each hexagon, and in the same relation to it, the hexagonal grid allows movement in more directions, and, therefore, is percieved to provide a more realistic representation of the real world, in which movement in any direction is possible.
Three-dimensional chess, by taking into account that the third dimension exists, also includes an element of the real world that is absent from ordinary chess.
However, I had not been aware of any attempt to devise a variant of chess that is both three-dimensional and hexagonal when I began work on this page. No doubt this is because such a variant would be too complicated to play, although since Fairy Chess is mostly applied to chess problems rather than over-the-board play, it would seem to me that this is not an insuperable obstacle.
I have, though, now attempted to search again for such a variant, and I found Hexagonal Raumschach on the Chess Variant Pages. However, this variant only stacks the hexagonal boards vertically, so that moves involving the vertical dimension are made as if on a regular chessboard instead of as in Hexagonal Chess.
The page mentions that other hexagonal 3-D variants exist, particularly more than one by Charles Gilman. A web search turned up other variants of his, including a square 3-D variant, but I couldn't find any information on his hexagonal 3-D variants.
The first question I had to ask myself, however, was if such a variant of Chess was even possible, and, if so, on what sort of board would it be played?
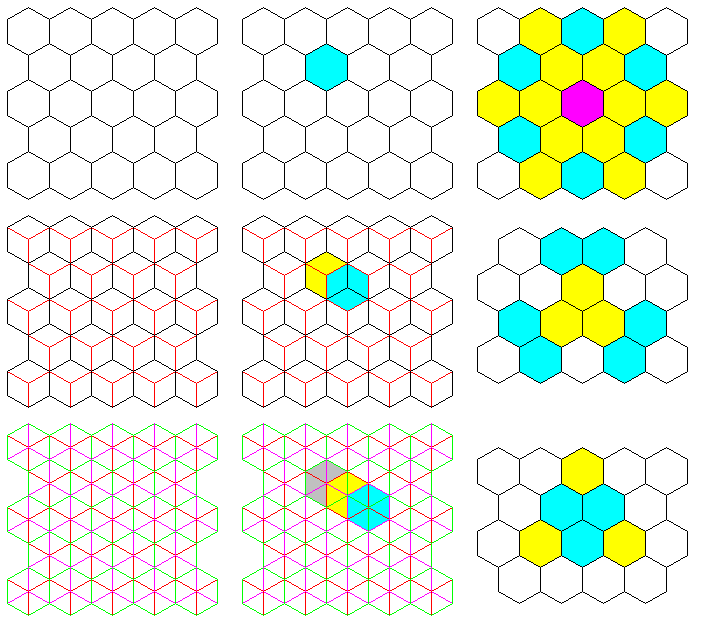
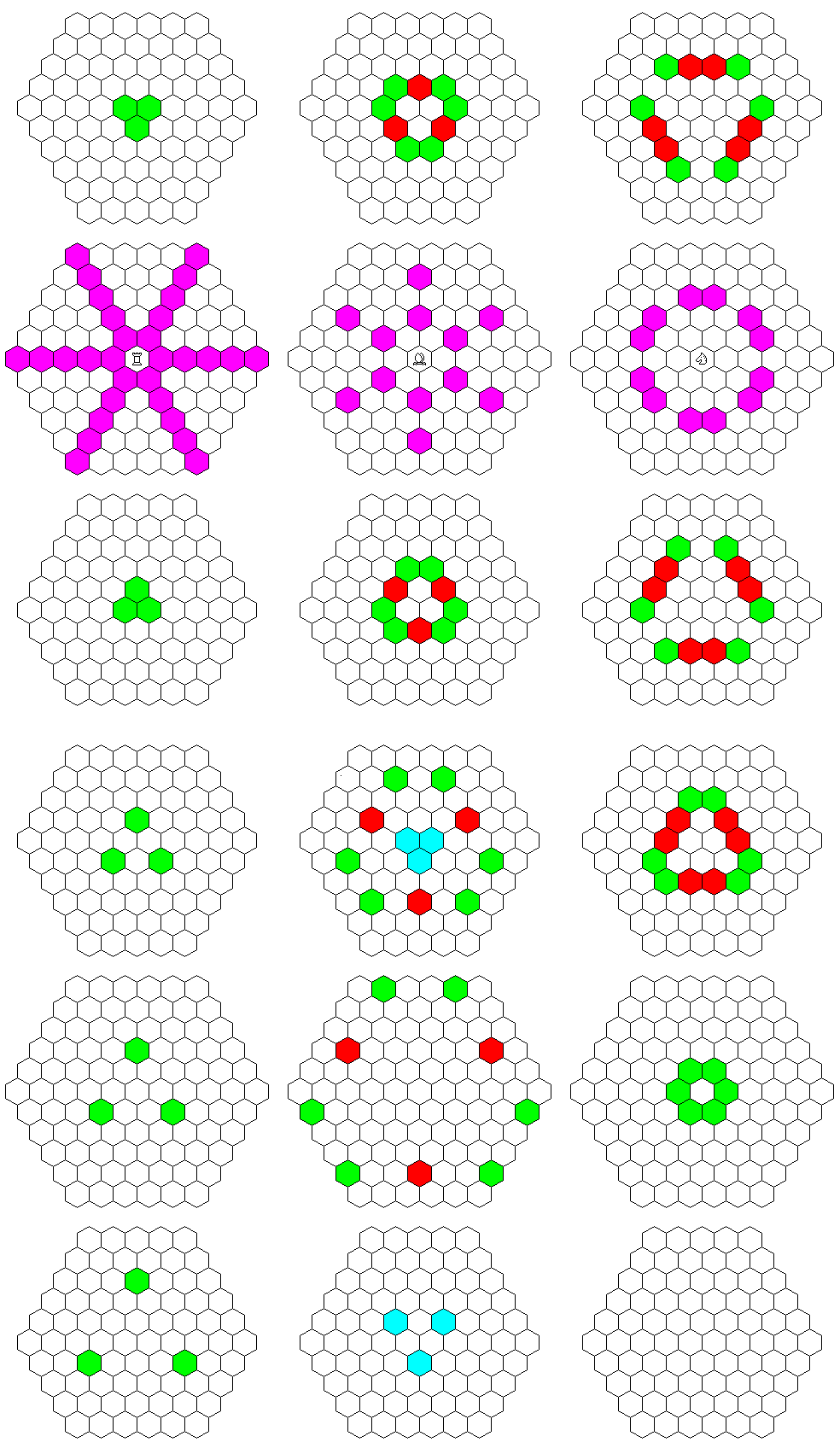
This diagram illustrates my investigation into those two questions:

The result is: Yes, hexagonal three-dimensional chess is possible. The boards, with regular arrays of hexagons on them, would need to be aligned in a repeating series of three horizontal displacements.
One starts with a board composed of regular hexagons as the base. The next board above it would be in the same orientation, of course, but with the centers of its hexagons so positioned as to be directly over half of the points on the base board where the corners of three hexagons meet.
Then the third board in sequence is positioned so that the centers of its hexagons are over the other half of the points on the base board where the corners of three hexagons meet. And the fourth board is aligned vertically over the base board, with the sequence repeating.
With a board constructed in this manner, in addition to hexagonal movement being possible on the plane of each board, hexagonal movement is also possible on planes oriented in three additional directions (as opposed to two additional directions for ordinary three-dimensional chess).
These planes all intersect an orthogonal line on one of the hexagonal boards that sit horizontally, and their vertical extent is in a perpendicular direction to that line which lies 30 degrees away from the vertical.
It may be possible to visualize the directions in which those planes go from looking at the diagram above; in the third column, starting from a central hexagon that is purple, the directions of orthogonal movement are shown in yellow, and the directions of diagonal movement are shown in cyan.
The diagram below shows a larger extent of a hexagonal three-dimensional chess board, and it shows what the moves of the rook, the bishop, and the knight would be upon it.
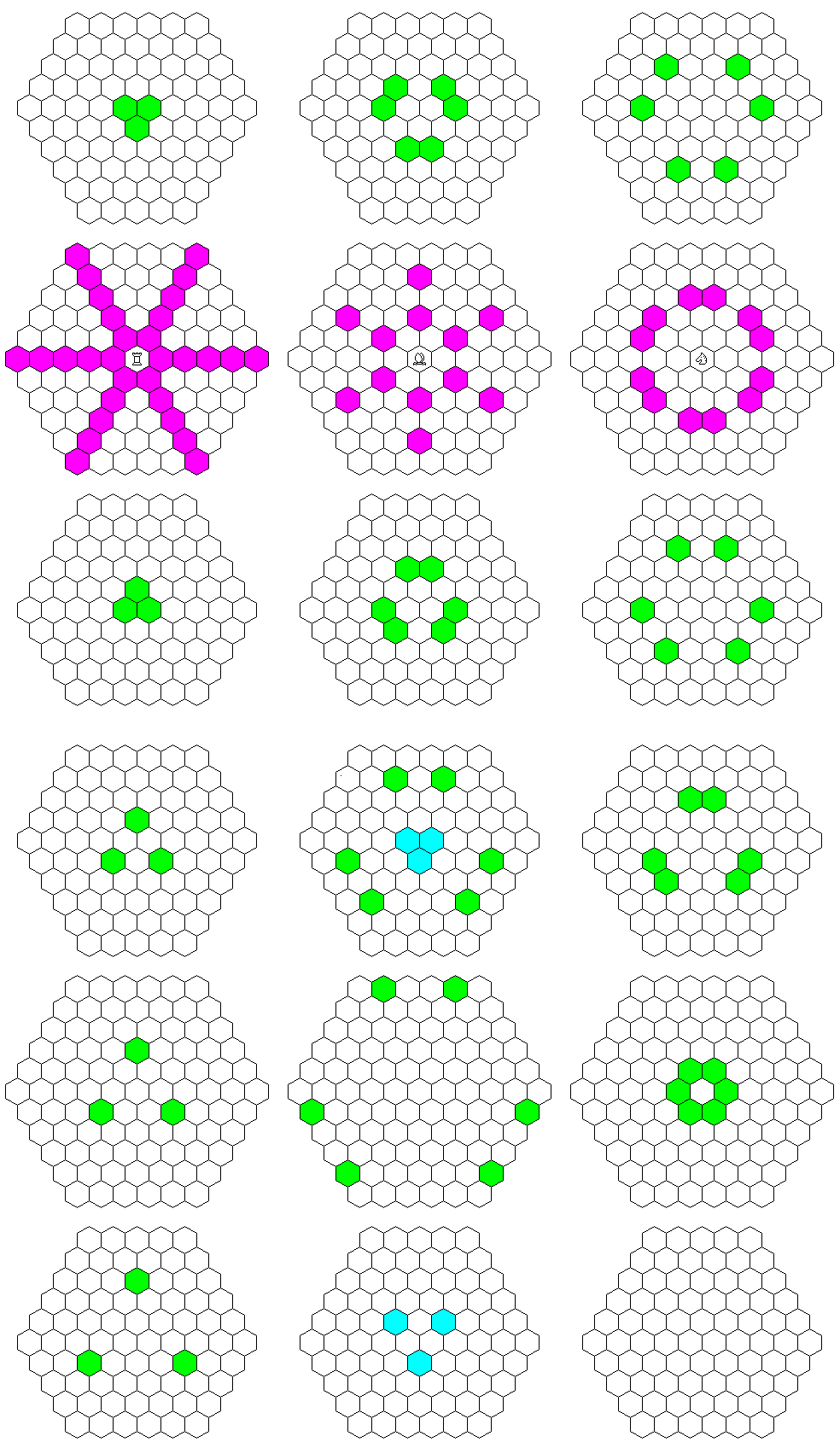
This may be a further aid to understanding.
However, the only real way to make these additional planes easier to understand is to illustrate this three-dimensional concept with a three-dimensional drawing. Therefore, one follows:
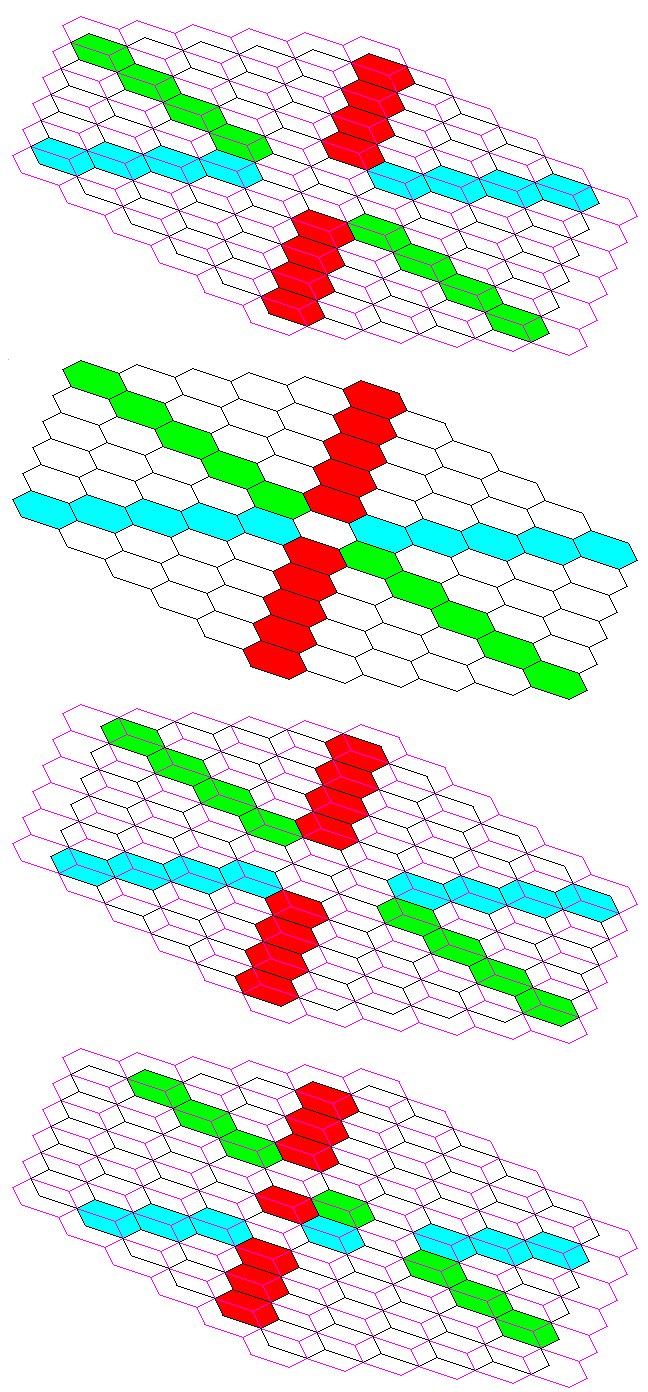
Red, green, and cyan are used to indicate the hexagons belonging to one example plane lying in each of the three possible directions; hexagons that belong to more than one such plane are left uncolored.
Purple, or mauve, (or they may be called by some, magenta) lines are in the positions of the lines around the hexagons in the second board in the diagram; as the intersections of these three-dimensional planes with the boards are in every case symmetric around the center, that, in addition to those lines, should make it possible to understand how the boards are stacked relative to each other.
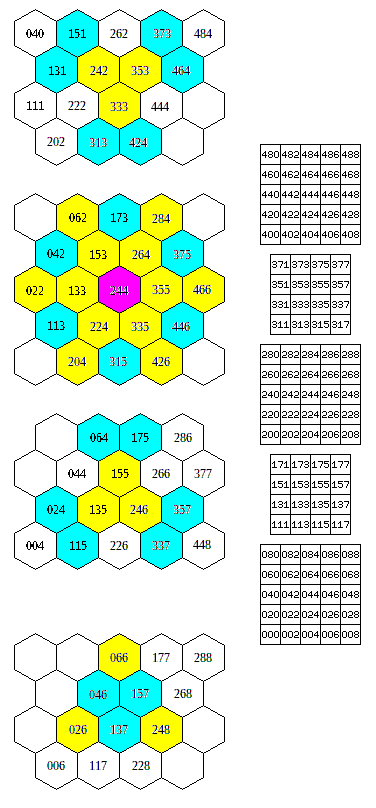
While the fact that the boards aren't simply stacked vertically means that conventional chess moves aren't the only three dimensional moves possible, there still remain, in addition to the additional partly vertical planes in which the cells on the various boards are arranged in a hexagonal array that we've seen above, equally valid partly vertical planes where the cells are arranged in the conventional square grid.
This is a consequence of the fact that the unit cell of the various hexagonal close packings of spheres is a cube.
Those planes are shown in the diagram below:
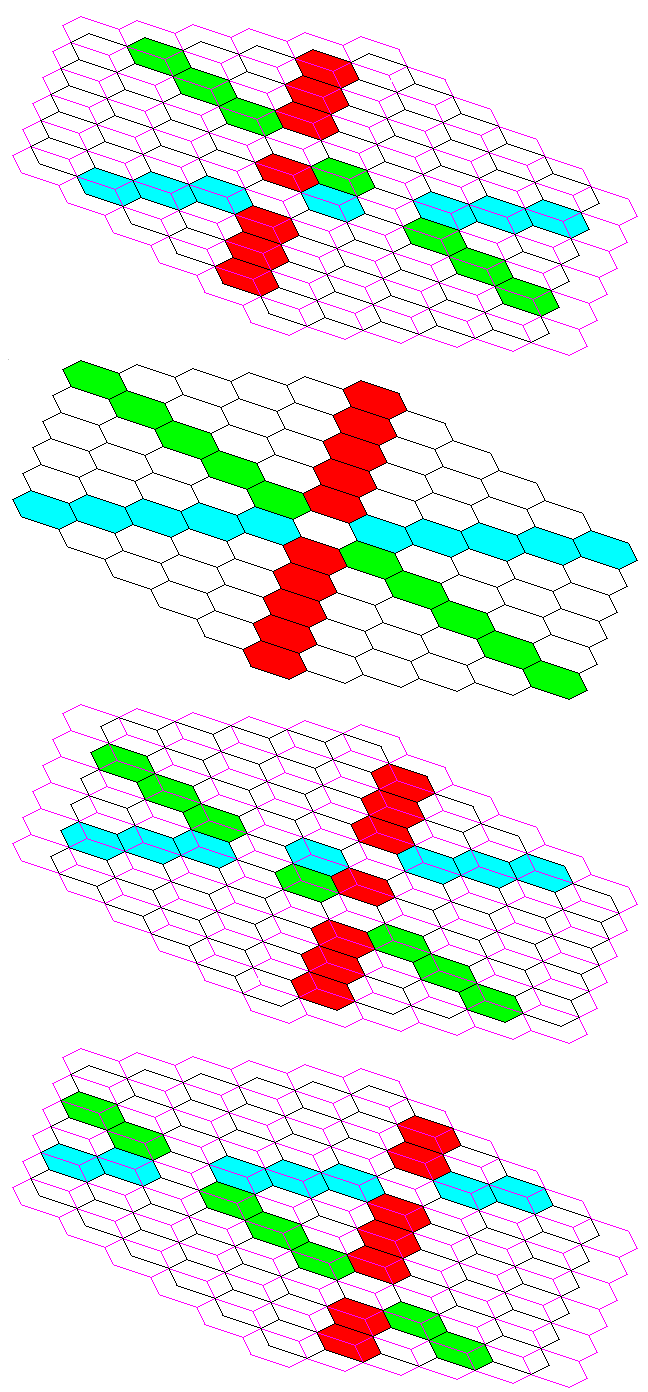
This is because the arrangement of hexagons follows the symmetry of the Face-Centered Cubic arrangement of items. Since it's a cubic arrangement, it follows that it should be possible to represent it with a stack of normal square chessboards. And this is indeed true, but alternate chessboards need to have the centers of their squares placed above the points where the corners of squares intersect on the chessboards above and below them.
This diagram shows, in red, the additional moves gained by the Bishop and Knight due to the ability to move as on the square chessboard in the additional planes shown above.
Interestingly enough, however, no Rook moves are added.
How the squares of that arrangement correspond to the hexagons of the arrangement previously described, something that at first sight seems almost unbelievable, is shown by the diagram below:
And by looking at the hexagonal three-dimensional chess board in this way, it appeared that for the conventional chess moves, possible along some planes, the board is divided into two halves; a piece can only cross over from one half to the other through a hexagonal move. But, in fact, that can't be possible, since an orthogonal move of one square is both a valid hexagonal move and a valid square move; while cubes have a threefold symmetry along their space diagonal axis, since any orthogonal line on the hexagonal board may also be a basis for a square board, there are square-board moves possible in directions that the square-board representation of the board does not make obviously visible.
One thing, though: the three-dimensional chess board in the diagram suggests the Body-Centered Cubic arrangement of cells, and yet all the crystallography textbooks will note that it is the Face-Centered Cubic arrangement of cells that corresponds to a close packing of spheres which, from some directions, has them arranged hexagonally within certain planes. What is going on here?
Basically, the answer is that the vertical spacing between the square planes differs from that which would produce a body-centered cubic arrangement. With a different spacing, such a three-dimensional chess board does correspond to the face-centered cubic arrangement, and the diagram below shows how this can be:
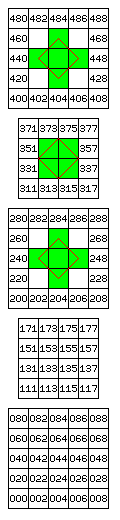
Squares belonging to one unit cell of the face-centered cubic arrangement are shown in green, and the boundaries of the unit cell are shown in red.
In the body-centered cubic arrangement, the distance between planes in the diagram is equal to one-half the distance between orthogonally adjacent cells in any one plane.
In the face-centered cubic arrangement, the distance between planes in the diagram is equal to one-half the distance between diagonally adjacent cells in any one plane, so, in effect, the vertical spacing is increased by a factor of the square root of two.
And this change in spacing has a material effect on what moves are possible. In the diagram below,
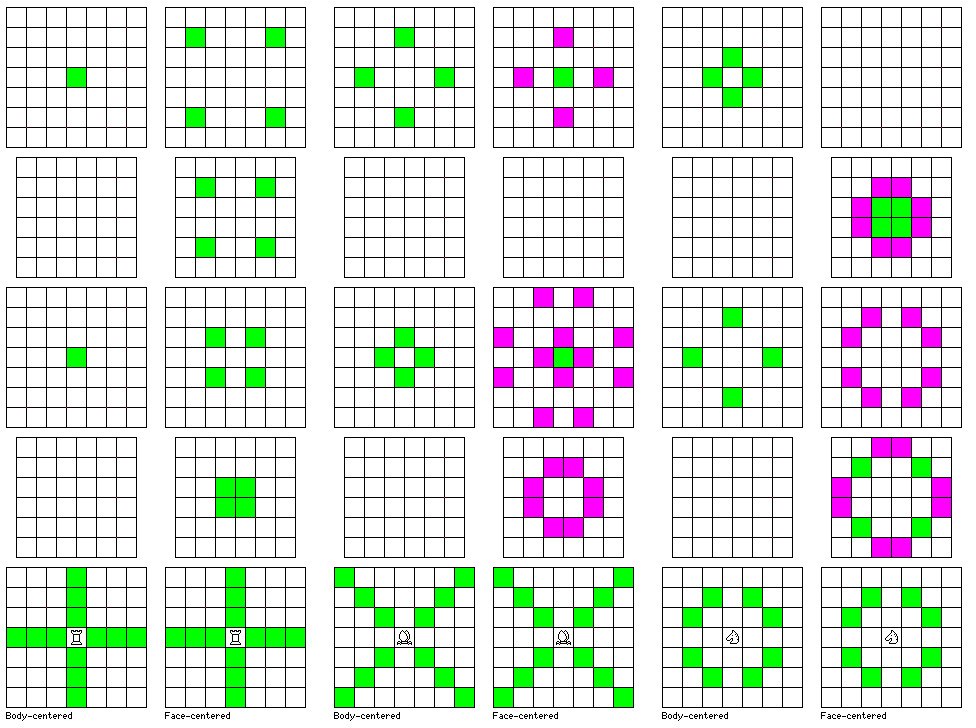
the difference between the possible three-dimensional moves of the Rook, Bishop, and Knight in the two cases is illustrated. The square-board moves are shown in green; the additional hexagonal-board moves are shown in purple, for the Bishop and Knight, for which this is applicable, in the face-centered cubic case, where the board corresponds properly to the hexagonal board.
Looking at the diagram for the Rook moves in the face centered cubic case gave me the clue to finally look up the information I needed to solve the mystery of the face-centered cubic arrangement, and make it easily understandable.
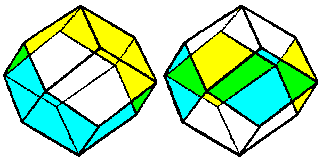
It turns out that the cells, represented either by hexagons or by squares on the playing boards, in which pieces are located can be thought of as having the shape of a rhombic dodecahedron.
This shape is the dual of the cuboctahedron, the 14-sided Roman die.
In the diagram above, the rhombic dodecahedron on the left has a belt of faces indicated by color whose surfaces form parts of the sides of a regular hexagonal prism. The remaining faces are part of the apex of a triangular pyramid; in additiion to being pointed in opposite directions, they are in opposite orientations.
Thus, it's clear how this corresponds to the way in which the hexagonal layers are placed for this division of space.
The rhombic dodecahedron on the right, on the other hand, has four faces in square orientation indicated by color. This time, the pyramidal sections at the top and bottom are, in comparison to the indicated faces, rotated by 45 degrees, and thus this can be seen as corresponding to the offset between layers of the square board - and the directions of the Rook moves in the applicable diagram.
Also, it may be noted that a regular 3-D chess board suffices for playing chess on the face-centered cubic lattice; all one has to do in order to obtain that geometry is to only use one color of squares, just as is done when playing checkers.
For further help in understanding and visualizing the Face-Centered Cubic symmetry, here are two other pages on my site which refer to it: the page on sphere packing, and the page about space-filling polyhedra.
Since one way to think of how the rhombic dodecahedron could be created would be to build a pyramid on each face of a cube, and then to adjust the heights of the pyramids so that the triangular faces of the pyramids on two adjacent square faces of the cube adjoining one edge of the cube are in the same plane, to form a diamond-shaped face of the rhombic dodecahedron, it's not surprising that each face of the rhombic dodecahedron corresponds to one edge of the cube.
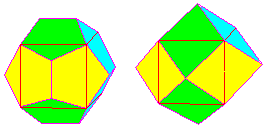
But what is amazing is that the pentagonal faces of the regular dodecahedron also each correspond to one edge of a cube, as the diagram above illustrates!
One limitation of a three-dimensional chess board based on the face-centered cubic geometry is that while there are planes within it that allow both chess moves between square cells, and chess moves between hexagonal cells, there does not seem to be any natural way to define genuinely three-dimensional moves, such as that of the Unicorn in Raumschach.
I have noted above on this page that the face-centered cubic symmetry can be thought of as being identical to the body-centered cubic symmetry, except for being stretched by a factor of the square root of two in one direction.
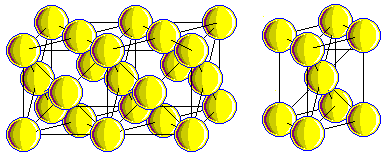
Here is another diagram illustrating this.
The face-centered cubic symmetry can also be related to the simple cubic symmetry by being stretched by a factor of two along the space diagonal of a cube; the diagram below illustrates this, among other things.
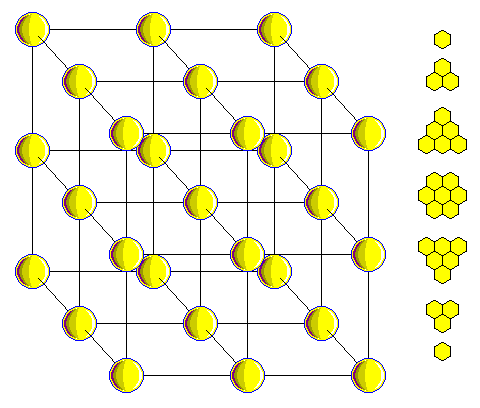
But that explains how one can slice a cubic lattice into multiple layers of points in a hexagonal layout in one of the three space diagonal directions. How is it that one can do so in all three?
Well, of course, the reason is that there is another relationship between the simple cubic array and the face-centered cubic array.
If a face-centered cubic array corresponds to all the black squares on a three-dimensional chessboard, then clearly it also corresponds to all the white squares, and so in addition to being a stretched face-centered cubic array, a simple cubic array is also the superposition of two face-centered cubic arrays without any stretching.
So now we can easily add hexagonal moves on the hexagonal planes within the cubic lattice to three-dimensional chess on the conventional board!
Well, there is still one problem. It turns out that now the Rook's move on a hexagonal plane is now identical to the Bishop's move on a square plane. So if we gave pieces both their own square moves, and their own hexagonal moves, the Rooks would suddenly become Queens!
But there is a cure. Give the Rook the hexagonal move of the Bishop, and give the Bishop the hexagonal move of the Rook. The Knight, on the other hand, can still recieve the hexagonal Knight's move as well without creating a conflict.