
Here, I am attempting to introduce another game, similar to Random Variant Chess in having as its goal to provide a game which has multiple random starting positions, but with all of them being symmetrical like the initial position of conventional Chess, rather than being "messy", as it were, as are the initial positions in Chess 960 (also known as Fischer Random Chess).
This is achieved by having a conventional layout, and using the random element to choose which types of pieces are to be replaced by other types of pieces with different moves, but similar strength.
The significant improvement in this game is that the board has been carefully modified to avoid disruptive changes to Castling.
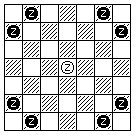
Thus, the first modification is that the regular 8 by 8 board is changed to one that is 8 squares deep by 10 squares wide, with Camels placed between the Knights and the Rooks. As the Camels can leap over the row of pawns in front as easily as Knights, this doesn't diminish the benefits of Castling, because it doesn't become necessary to advance Pawns to let new pieces out before Castling can take place.
But additional new pieces still need to be added in order to produce the extent of change that is desired. So an additional four squares are added to the board behind the King, Queen, and Bishops of each side. This allows the other new pieces to have an opening to reach the board that comes about from advancing the center Pawns to control the center and allow the Bishops and the Queen to be brought into play.
Finally, to maintain the balance between squares and men, four more squares are added to the board on each side. Since a Pawn could conceivably capture a piece in the wings of the board, a Pawn reaching the furthest square on one of those wings, from which it could not advance except by a capture, also promotes. As well, in the four central files of the board, Pawns must advance to the very end to promote, to the final rank that is only four squares wide.
Pawns promote only to one of the pieces that were part of the initial array (other than to a Pawn or to a King) chosen randomly for the variant being played.
Also, the system of choosing a random variant has been considerably simplified compared to those shown for Random Variant Chess; here, it has been designed so that a variant can be chosen by the simple throw of dice, without the need for special equipment.
While the final version of this game, Chess 2016, is the one I primarily recommend, it may be easier to follow the explanation of that game by looking first at a simpler version which I initially developed:
On the bottom of a later page, I note that enlarged versions of Chess tend to prevent the King from obtaining a secure position after Castling, and, thus, alter the game significantly. There, I show an enlarged version of Chess which puts most of the new pieces on the wings of the board to address the issue.
Below is an array which deals with the issue in another manner:

As with the variant shown there, the row of pieces behind the pawns are:
Rook, Camel, Knight, Bishop, Queen, King, Bishop, Knight, Camel, Rook
so the conventional array is only extended by the Camel, which can also leap over the Pawns in front without requiring the line to be broken by a Pawn advance.
But in this case, the extra pieces other than the Camels are put on new squares in a rank behind the central part of the normal initial array. Additional squares are also added on the wings, so that, as with the normal chess board, there are pieces on exactly half of the squares on the board in the initial position.
These extra pieces, in the default array, are:
Tiger, Man, Cannon, Tiger
The Camel is a 1-3 leaper. That is, its move is similar to that of the Knight, but instead of being displaced two squares in one direction, and one square in a perpendicular direction, it is displaced three squares in one direction, and one square in a perpendicular direction.
The Tiger moves as a Bishop, but captures as a Knight.
The Cannon is the piece found in Chinese Chess. It moves like a Rook, but when it captures, it captures along Rook lines, but it can only capture the second man from it, with one man of either color in between.
The Man moves one square in any direction. This is like a King, but this piece does not Castle, nor does capturing it have any special significance.
So that Castling in this game is as much like Castling in regular Chess as possible, here the King moves three squares to the right or left when Castling. Neither of the two squares it passes over may be attacked by an enemy piece in order for Castling to be allowed. The Rook moves to the square immediately beyond the Castled position of the King. As in normal Chess, neither the King nor the Rook may have been moved before in the game.
As with Random Variant Chess, some of the pieces in the initial array are replaced on a random basis. To make things as simple and convenient as possible, I use the 56 possible visible combinations of three ordinary dice as the basis to choose what to replace.
When all three dice have different numbers on them, the replacements are as follows:
Lowest Number Middle Number Highest Number Man becomes Cannon becomes Queen becomes 1: Walker 2: Duchess 3: Monarch 2: Wazir 3: Princess 4: Leo 3: Elephant 4: Camelrider 5: Griffin 4: Fers 5: Lady 6: Empress
Not all the combinations are possible, of course, but I view that as a minor matter, well worth accepting for the convenience of using standard equipment for randomization.
The Wazir moves one step orthogonally.
The Fers moves one step diagonally.
The Walker moves without capturing like the Wazir, and captures without otherwise moving like a Fers. Thus, it's like a Pawn that can move in any direction instead of just forwards.
The Elephant moves one step diagonally, or one step forwards.
The Princess moves like a Bishop or like a Knight.
The Duchess moves like a Bishop or like a Zebra (see below).
The Lady moves like a Bishop or like a Giraffe (see below).
The Camelrider moves one or more steps in the same direction, each step being the move of the Camel.
The Empress moves like a Rook or like a Knight.
The Griffin moves one step diagonally, followed by two or more steps orthogonally. Thus, while it cannot move to the squares a Knight can reach, it can move to the squares a Camel can reach. Unlike the Knight or the Camel, it is blocked by pieces on the earlier steps of its path, including the first two squares on which its move cannot end.
The Leo moves like the Queen, and captures on squares on Queen lines which involve jumping over exactly one man of either color; thus, it is like a Cannon, but it operates on Queen lines instead of Rook lines.
The Monarch moves like a Rook or a Camel.
When two of the dice have the same number on them, with the third different, the substitutions are as follows:
Paired Dice Remaining Die
Tigers become:
1-1: Lions 1: Man becomes Walker (or Tigers become Walkers instead of Men)
2-2: Zebras 2: Man becomes Wazir (or Tigers become Wazirs instead of Men)
3-3: Giraffes 3: Cannon becomes Princess
4: Cannon becomes Camelrider
Man becomes: 5: Queen becomes Griffin
4-4: Lion 6: Queen becomes Empress
5-5: Zebra
6-6: Giraffe
and the Tigers become Men (or, possibly, Walkers or Wazirs).
The Zebra moves three squares in one orthogonal direction, and two squares in a perpendicular orthogonal direction, ignoring intervening pieces. Thus, its move is similar to that of a Knight, except longer, and, like a Knight, it changes color with each move.
The Giraffe moves four squares in one orthogonal direction, and one square in a perpendicular orthogonal direction, ignoring intervening pieces. Thus, its move is similar to that of a Knight, except longer, and, like a Knight, it changes color with each move.
The Lion moves, without capturing, like a Knight, and captures, without otherwise moving, like a Bishop. Thus, it is the inverse of a Tiger.
Finally, when all three dice show the same number, the substitutions are as follows:
1-1-1: No substitutions. 2-2-2: Queen becomes a Man. Man becomes a Nightrider. 3-3-3: Queen becomes a Rhinoceros. 4-4-4: Cannon becomes a Princess. 5-5-5: Queen becomes an Empress. 6-6-6: Man becomes a Tiger, Tigers become Men.
The Rhinoceros moves from one to eight steps. The first step is diagonal or orthogonal. Succeding steps alternate between being orthogonal and diagonal, with each step representing the same 45 degree change, clockwise or counterclockwise, in direction. Thus, this piece goes around in circles.
The Nightrider moves one or more steps in the same direction, each step being a Knight move.
It is thought that fifty-six possible starting positions should be enough to ensure the game does not become dependent on opening theory. As with the original Random Variant Chess, the array remains symmetric, unlike the case for such variants as Chess 360 (also known as Fischer Random Chess). Now, though, the board is no longer rectangular, but as noted above, Castling is more exactly preserved from regular Chess.
For additional variation, tournament organizers can choose to interchange Knights and Camels. Unlike interchanging Knights and Bishops in regular Chess, this does not change which Pawns need to be moved to open up the position to let the Bishops out. They can be interchanged in all games, or only when the total of the three dice is one of either odd or even - and that selection can alternate between rounds, so that all 112 possible openings can be brought into use.
Here, the initial position is chosen using five dice, three identical white dice, and one green die and one red die, these being the common standard colors in which dice are readily available. Of course, other colors can be used as well, provided agreement exists, to accomodate either the availability of equipment, or the most common form of color-blindness.
Alternatively, color-blindness can be accomodated if one, but not both, of the red and green dice is a transparent die, with the other one being opaque, or if they otherwise differ in size or style. As red transparent dice may possibly be slightly more widely available than green transparent dice, let it be the convention that it will be the red die that is not uniform with the green and white dice if this step is taken.
The three white dice have 56 visibly different possible rolls, while the green and red dice have 36 possible rolls; 56 times 36 is equal to 2016, hence the name of this variant.
Is the world ready for this version of Chess? Will it even be ready four years from the time of this writing (which, being the year 2012, looks to 2016 as four years in the future)?
Understanding how Chess 56 works will help in understanding this variant, which is built on the same principles.
The green die determines the substitution for the Queen:
1: The Queen remains a Queen. 2: The Queen becomes a Man, the Man becomes a Nightrider. (See below) 3: Empress 4: Griffin 5: Leo 6: Monarch
In the event that the Man is to have another piece substituted for it, then when 2 is rolled on the green die, the Queen becomes that piece instead, with the Man still becoming a Nightrider.
The red die determines the substitution for the Cannon:
1: The Cannon remains a Cannon. 2: Princess 3: Camelrider 4: Duchess 5: Lady 6: Archbishop
The Archbishop moves either as a Bishop or as a Wazir; that is, it moves diagonally, or it can move one step orthogonally.
The three white dice determine substitutions for other pieces.
If two dice are the same, the rolls are interpreted as follows:
Paired Dice Remaining Die
Tigers become: Man becomes:
1-1: The Tigers remain Tigers. 1: Tiger
2-2: Men 2: The Man remains a Man.
3-3: Lions 3: Lion
4-4: Zebras 4: Zebra
5-5: Giraffes 5: Giraffe
6-6: Vaos 6: Vao
Note how both the Man and the Tiger, both being minor pieces of about the same strength, can be replaced by the same six possible pieces, but because the roll must have two dice with one number, and a third die with another number, they cannot both have the same substitute.
The Vao moves like the Cannon in Chinese Chess, but along Bishop lines instead of Rook lines.
If all three dice are different, then the rolls are interpreted in this fashion:
Lowest Number Middle Number Highest Number
Man becomes Camels become Tigers become
1: Walker 2: Giraffes 3: Zebras
2: Wazir 3: Zebras 4: Giraffes*
3: Zebra* 5: Lions
4: Giraffe Knights become 6: Vaos
4: Giraffes
5: Zebras
and Camels become Knights
There is one special case for the substitutions marked by an asterisk.
Because all three numbers are different, only one of the Man, Camel, or Tiger can be replaced by a Zebra, and only one of the Man, Knight, or Tiger can be replaced by a Giraffe.
However, the replacement of a Camel by a Giraffe, or of a Knight by a Zebra, are not protected fully in this way.
In the case where Camels are replaced by Giraffes, while the Man cannot be replaced by a Giraffe since 4 is not a lower number than 2, it could be that the dice could direct that the Tigers are to be replaced by Giraffes. In that case, the Tigers are to be replaced by Wazirs instead. As 2 is not less than 2, the dice cannot direct that the Man is to be replaced by a Wazir.
In the case where Knights are replaced by Zebras, while the Tigers cannot be replaced by Zebras since 3 is not a higher number than 5, it could be that the dice could direct that the Man is to be replaced by a Zebra. In that case, the Man is to be replaced by a Lion instead. As 5 is not greater than 5, the dice cannot direct that the Tigers are to be replaced by Lions.
If all three dice are the same, then the following are the additional substitutions to be made:
1-1-1: Camels become Giraffes. 2-2-2: Man becomes Zebra, and interchange Knights and Camels. 3-3-3: Man becomes Giraffe, and interchange Knights and Camels. 4-4-4: Tigers become Lions, and interchange Knights and Camels. 5-5-5: Tigers become Vaos, and interchange Knights and Camels. 6-6-6: Interchange Knights and Camels.
This allows the roll of five dice to create a wide variety of opening positions, all symmetrical and balanced.
As, however, some might find the description of the substitutions made by the three identical dice to be complicated or confusing, a table below is given which shows explicitly what substitutions are to be made for each of the 56 possible combinations of the three identical dice.
Tigers Man Camels Knights
1-1-1: Tigers Man Giraffes Knights
1-1-2: Tigers Man Camels Knights
1-1-3: Tigers Lion Camels Knights
1-1-4: Tigers Zebra Camels Knights
1-1-5: Tigers Giraffe Camels Knights
1-1-6: Tigers Vao Camels Knights
1-2-2: Men Tiger Camels Knights
1-2-3: Zebras Walker Giraffes Knights
1-2-4: Wazirs Walker Giraffes Knights
1-2-5: Lions Walker Giraffes Knights
1-2-6: Vaos Walker Giraffes Knights
1-3-3: Lions Tiger Camels Knights
1-3-4: Giraffes Walker Zebras Knights
1-3-5: Lions Walker Zebras Knights
1-3-6: Vaos Walker Zebras Knights
1-4-4: Zebras Tiger Camels Knights
1-4-5: Lions Walker Knights Giraffes
1-4-6: Vaos Walker Knights Giraffes
1-5-5: Giraffes Tiger Camels Knights
1-5-6: Vaos Walker Knights Zebras
1-6-6: Vaos Tiger Camels Knights
2-2-2: Tigers Zebra Knights Camels
2-2-3: Men Lion Camels Knights
2-2-4: Men Zebra Camels Knights
2-2-5: Men Giraffe Camels Knights
2-2-6: Men Vao Camels Knights
2-3-3: Lions Man Camels Knights
2-3-4: Giraffes Wazir Zebras Knights
2-3-5: Lions Wazir Zebras Knights
2-3-6: Vaos Wazir Zebras Knights
2-4-5: Lions Wazir Knights Giraffes
2-4-6: Vaos Wazir Knights Giraffes
2-5-6: Vaos Wazir Knights Giraffes
2-6-6: Vaos Man Camels Knights
3-3-3: Tigers Giraffe Knights Camels
3-3-4: Lions Zebra Camels Knights
3-3-5: Lions Giraffe Camels Knights
3-3-6: Lions Vao Camels Knights
3-4-4: Zebras Lion Camels Knights
3-4-5: Lions Zebra Knights Giraffes
3-4-6: Vaos Zebra Knights Giraffes
3-5-5: Giraffes Lion Camels Knights
3-5-6: Vaos Lion Knights Zebras
3-6-6: Vaos Lion Camels Knights
4-4-4: Lions Man Knights Camels
4-4-5: Zebras Giraffe Camels Knights
4-4-6: Zebras Vao Camels Knights
4-5-5: Giraffes Zebra Camels Knights
4-5-6: Vaos Giraffe Knights Zebras
4-6-6: Vaos Zebra Camels Knights
5-5-5: Vaos Man Knights Camels
5-5-6: Giraffes Vao Camels Knights
5-6-6: Vaos Giraffe Camels Knights
6-6-6: Tigers Man Knights Camels
There does remain the interaction where 2 is rolled on the green die.
That can be understood in one of two ways: