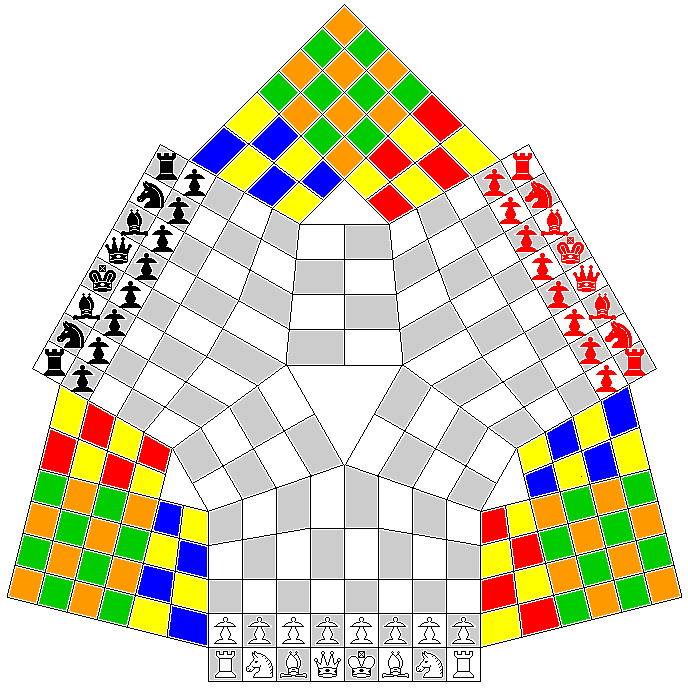
The board for the Chinese Game of Three Kingdoms distorts the square chess-board by squeezing 540 degrees into 360 degrees at its center. Several three-player versions of regular Chess apply the same distortion to the regular chessboard, one of which was devised by the same Robert Zubrin who proposed a more effective means of voyaging to Mars.
An early version of three-player Chess due to one Henry J. Self applied the same basic distortion, but left a hole in the center of the board so that no peculiar rules about the moves the pieces might make from the center would be needed. The board I illustrate below leaves a smaller hole in the center for the same purpose.
Alternatively, a board for three-player chess devised by one M. Coqueret stretches 270 degrees to fill 360 degrees. This, as with the five-player board I devised on a previous page, allows Bishops to change color with a circuit around the board. (This is not a necessary consequence of stretching 270 degrees to fill 360 degrees; it would not happen if each side of the triangle consisted of an odd number of squares so that all three corners could be the same color consistently.)
I thought it might be interesting to combine both approaches in a single board. This does, however, result in a board that is somewhat large, having 240 squares:

Bishops maintain their colors in the central part of the board, but in the loops in the wings they can change color. Note that the bishops, once the pawns are out of the way, attack each other on their starting squares - of opposite color.
As in normal Chess, Pawns can make a double-step first move, and are subject to en passant capture when they do so. As they promote on the 12th rank instead of the 8th on this board, there seems no reason to deprive them of this privilege.
A Pawn can capture into the wings. The consequences of this fact are dealt with by the following rules:
To illustrate these rules by example, it will be helpful to establish some form of algebraic notation for this board. The following, retaining the notation used for conventional Chess as far as possible, might be usable:

Only part of the board is describable algebraically from any one player's viewpoint, and so, as shown here in the case of the player with the White pieces, when the player's pieces are in an area inaccessible to that player's own algebraic notation, the square is described in that of another player, with a prefix (b: black, r: red, w: white) used to indicate which player's algebraic notation is used.
Come to think of it, though, it would be possible to extend White's algebraic notation to cover the whole board without having to have more designations for files than there are letters in the alphabet (of course, that, too, is possible; one could use aa, ab, ac, and so on).
One possible scheme would be the following, which would increase the number of files by 2, adding a t-file and an o-file, illustrated below in what is more a table than a diagram:
bu2
u21
bv2 bv3 rm2
u20 v20 n20
bw2 bw3 bw4 rl3 rl2
u19 v19 w19 m19 n19
bx2 bx3 bx4 bx5 rk4 rk3 rk2
u18 v18 w18 x18 l18 m18 n18
by2 by3 by4 by5 rj5 rj4 rj3 rj2
u17 v17 w17 x17 k17 l17 m17 n17
bz2 bz3 bz4 bz5 ri5 ri4 ri3 ri2
u16 v16 w16 x16 k16 l16 m16 n16
ba1 ba2 ba3 ba4 ba5 ba6 rh6 rh5 rh4 rh3 rh2 rh1
t15 u15 v15 w15 x15 y15 j15 k15 l15 m15 n15 o15
bb1 bb2 bb3 bb4 bb5 bb6 rg6 rg5 rg4 rg3 rg2 rg1
t14 u14 v14 w14 x14 y14 j14 k14 l14 m14 n14 o14
bc1 bc2 bc3 bc4 bc5 bc6 rf6 rf5 rf4 rf3 rf2 rf1
t13 u13 v13 w13 x13 y13 j13 k13 l13 m13 n13 o13
bd1 bd2 bd3 bd4 bd5 bd6 re6 re5 re4 re3 re2 re1
t12 u12 v12 w12 x12 y12 j12 k12 l12 m12 n12 o12
The odd thing about this scheme is that, in White's notation, ranks and files change places when one crosses from the Kingside to the Queenside of the two opponents.
Because of the central hole in the board, so that it is never the case that the number of squares meeting at a corner is different from four, except where the corner is on the edge of the board so that some of the four squares that would meet there are not part of the board, there should be no ambiguity in the moves of the pieces. However, to ensure clarity, I will note that a Knight on the square h5 can move to f4, g3, i3, j4, f6 and g7; a Knight on the square h6 can move to f5, g4, i4, j5, k7, g8 and f7; a Knight on the square e5 can move to c4, d3, f3, g4, g6, f7, d7 and c6; and a Knight on the square e6 can move to c5, d4, f4, g5, g7, f8, and re5: but not to either rf6 or c7.
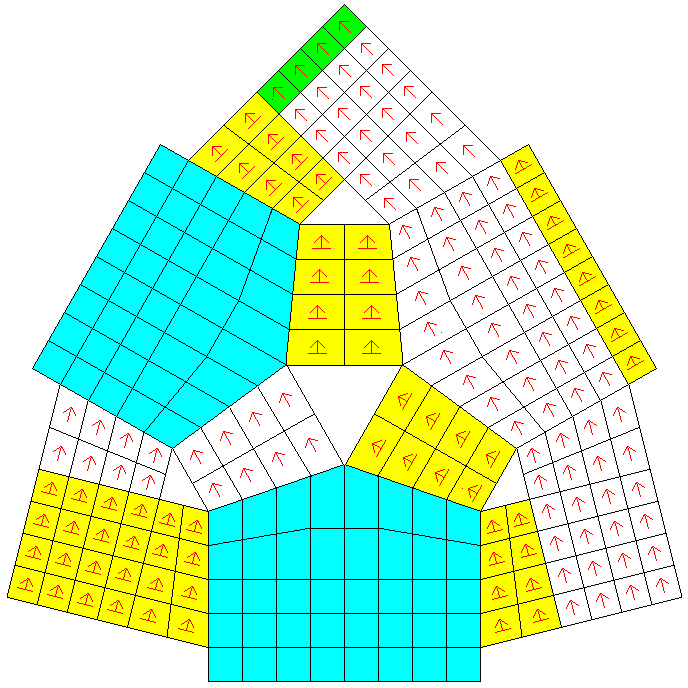
In the diagram, the squares on which White's pawns may move orthogonally in all directions, and capture diagonally in all directions, that is, moving as Wazir-movers/Fers-capturers or Berolina Pawns, are shown in light blue-green (or green); the squares on which White's pawns can move sideways in addition to their normal move are shown in yellow, the squares on which they have only their normal move are shown in white, and their promotion squares are shown in green.
In any case, suppose that a White Pawn is on a3; then it can capture an enemy piece on z4 in the wings as well as on b4. On z4, it would be able to move sideways to y4 or a4 as well as advancing to z5, or capturing on y5 or a5.
A White Pawn on x7 would only have a forwards move to a8, and capturing moves to a9 or a7; diagonally forwards from its point of view, but backwards in the case of a7 from the point of view on the main board.
Also, with a system of algebraic notation, it is possible to see how White's Queen Bishop, on its black home square of c1, can attack the Black Bishop on the white square c12; the line of attack goes through the black squares c1, b2, and a3; then the blue squares z4 and y5; then the yellow squares x6 and w7; and finally the white squares a10, b11, and c12.
When three players are playing, the King is always to the right of the Queen. Two players can also use the board; in that case, Black's King is on the left of the Queen, and the players are seated so that the Queensides of the two players are closer together, while the Kingsides have the part of the board where the absent third player would be between them. The simplest way to achieve that, from the array shown in the diagram above, is to remove the Red pieces, and exchange Black's King and Queen.
The order of move is counter-clockwise, White, then Red, then Black.
Incidentally, if one removes all three back ranks, the board that remains can be thought of three smaller boards, suitable for another form of three-player Chess, and somewhat distorted, stuck together.
Of course, while the wings on the board were added because the possibilities they create are interesting, when two or three players are playing on this board, it is also possible, by agreement, to eliminate this part of the board from play. In that case, Bishops would not change color, and Pawns would no longer be allowed to move sideways or backwards (until, of course, they had promoted to other pieces). This would simplify the game to make it an ordinary form of Chess for three players.
Next, however, we will examine a case where the loops on the wings can no longer be ignored, as they provide locations for the starting arrays of additional players.
While one thing one might think that the one thing this board could not possibly be used for is four-player chess, since in a partnership game, it is sufficient that the two partnerships be equal, even if the two players within each partnership are not, one could have one player in each partnership playing with a conventional array, and the other playing using a starting array arranged for a corner of the board.
Six players can also play as three teams of two partners; in that case, the side teams arrange their pieces as for the three-player game, and their corner partners are opposite them. Order of move is counter-clockwise.
Possible colors for the pieces of the players in partnership would be yellow for White's partner, blue for Black's partner, and green for Red's partner.
With four players as two teams of partners, the two edge players arrange their pieces as for the two-player game, and their corner partners are in both cases on their Kingside. (White King on e2, Black King on bd1, White's partner's King on n2, Black's partner's King on bu2) While an order of move such as White, Black's partner, Black, White's partner would be required for full symmetry between sides, this would complicate the game by allowing each partnership two turns before the other partnership may play; thus, White, Black's partner, White's partner, and Black is the order of move instead, despite the fact that this means the move of a player in the Black partnership is always followed by the move of a like-moving player in the opposite partnership, while the move of a player in the White partnership is always followed by the move of a player with the other class of initial array, corner instead of side, or side instead of corner (not to be confused by the two possible arrangements of the corner arrays, to be described next).
Having a symmetrical array with both bishops on the same color would not even be a problem with this board, as they would have opposite colors once they emerged onto the main board if they did so each on its own side!
An example might be:
The Pawns on l5, m5, n5 and n4 would have the same normal direction of forwards movement as White pawns, and those on k2, k3, k4 and l2 would have the same normal direction of forwards movement as Red pawns. (Note that this means they must be distinguishable or orientable.)
This array has the form:
N P P P P N B P P B Q R P P R K
An alternate array, requiring only one type of Pawn for each player with a corner array, and thus not requiring distinctive or orientable Pawns, would be one of the form:
P P P P P P P P N R R B N B Q K
In each of these arrays, the King is, of course, located on the orange square that is at one of the three extreme corners of the board, n2, u2, or bu2.
Upon reflection, it seems that the alternate array is the one to recommend, at least for the four-player game. For the six-player game, however, the first array mentioned has the virtue of pointing the Pawns of one player's partner equally at the arrays of both that player's opponents. If, however, due to the lack of suitable equipment, the alternate array is employed for the six-player game, then the arrays of the corner players are so oriented that they face counter-clockwise.
The movement and promotion rules for the Pawns on l5, m5, n5 and n4 would be analogous to those for the Pawns of the players at an edge of the board, but they would be different in some respects. Specifically, the location of the promotion squares would be different, and the areas in which the Pawns temporarily gained additional powers of movement would be different.
As in normal Chess, Pawns would have a double-step first move, and be subject to en passant capture. Given that they promote on the 20th rank, as we shall see, allowing them the privilege of a double step on the first move is little enough.
The rules are sufficiently complicated that another diagram is required; note that the arrangement shown in the diagram may have to be mirror-reflected, in addition to being rotated, to show show the movement rules for groups of Pawns other than those which start on l5, m5, n5, and n4. In particular, a reflection about the vertical axis followed by a 120 degree counterclockwise rotation would be required to show the movement rules for the Pawns on the same team which start on k2, k3, k4 and l2.
If the alternative array were used, reflections would not be required for the six-player game, in which all Pawns would be pointed counter-clockwise, but a reflection would still be required to obtain the plan of movement for Black's partner's Pawns in the four-player game, since in that game, for symmetry, the array would be set up in a reflected manner so that Black's partner's Pawns would be pointed clockwise.
Note that since the pawns of the corner players have only the normal power of movement on their promotion squares, promotion is not optional for those players' Pawns. Also, note that the corner players have the disadvantage that their Pawns start on their 3rd and 4th ranks, and promote at the 20th rank, while the edge players have their Pawns starting at the 2nd rank, but promoting at the 12th rank (which, of course, is still a longer distance than the 8th rank of normal Chess). As well, it may be noted that while Pawns belonging to an edge player will undergo temporary promotion to gain first a sideways move, then movement in all directions, while still being restricted to orthogonal movement and diagonal capture, in the normal course of their advance to their promotion rank, while Pawns belonging to a corner player will only experience this if captures take then from their normal files.
Also, it should be made explicit that the intent of these rather complicated rules is that the movement of a particular kind of Pawn on the board is to always depend only on its location, and never on its history. Thus, for the four Pawns whose movement is described by the diagram above, a move from v6 to v7, or from b6 to b7, or from bx5 to bx4 is always a forwards move whether, for example, in the third case, the Pawn reached bx5 from rj5 or by5; and, equally, a move from bz4 to bz3 is always a forwards move, so that one of these Pawns on bz4 can move forwards to bz3, sideways to ba4 or by4, and capture on ba3 and by3, even if its past history involved reaching the square by such a route that the rightwards sideways direction might seem to be forwards. As the rules are complicated, arrows have been included in the diagram above to indicate the forwards direction for those squares to which it applies. There are many cases where, despite the forwards direction being indicated, movement in that direction is not possible: in addition to the promotion squares, this is true of the squares i5, j5, e6, e7, ba6, rh6, bz2, by2, y5, z5, and rh1 on all of which sideways motion (and capture diagonally forwards in one direction) is possible.
Also, when the alternate layout is used, just as the algebraic notation is used from the perspective of each of the side players, to use (for White's partner in the four-player game, and for any of the corner players in the six-player game) ranks 8 through 11 of the i through o files (in the case of Black's partner in the four-player game, for whom the symmetry would be flipped, that would be ranks 8 through 11 of the t through z files) would be used to describe what are referred to, from White's perspective, as ranks 6 through 12 of the e through f files (with ranks becoming files and files becoming ranks). Absent the alternate layout, since two groups of Pawns have two different forwards directions, it is not clear what form of algebraic notation would be native to the corner players.