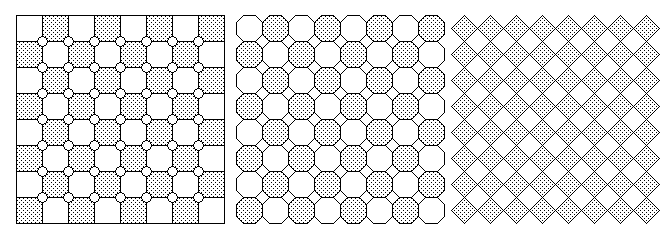
The images below show three possible boards for the game discussed here, which may also be played on a conventional board, provided that it is somewhat oversized for the pieces used:

The basic idea on which the game I propose is based is one that occurred to me as a child looking at a chessboard, and I suspect that it has occurred to many. I am surprised that I have not been able to find an instance of either a game or at least a problem theme in Fairy Chess based on it, but it's certainly possible that I have missed one. (The Bishop-Blockers of ECHECS+ are the only example I could find of the use of the specific portion of the chessboard I wish to make use of, and Alice Chess, although not all that similar, still could be said to be related, since it deals with Chess on two linked boards.)
The basic idea is that pieces moving diagonally may stop at odd half-steps, and end their move on one of the points of the chessboard, where the pieces are located in Hsiang Ch'i or the stones are placed in Wei Ch'i (or Go).
Thus, to quote H. P. Lovecraft, the pieces can move "not in the spaces we know, but between them".
Some elaboration on that basic idea is, of course, required to make a game out of it.
The final rule can be understood by considering that having dealings with the spirit world is considered disreputable, and thus entering it is something the King cannot do when he is watched by an enemy. But evidence brought back from the spirit world is notoriously unreliable, which is why one does not lose as soon as one's King is checked on a point. Note that this means a half-step diagonal move cannot be used for escape from checkmate on the main board, but it can still be used, and must be used if no other alternative exists, to escape from stalemate. If that rule is not needed to prevent checkmate from being too difficult, however, setting it aside by mutual agreement might become the rule, as it is a somewhat complicated one. Also note that the two pieces to which the Pawn is allowed to promote to on the last row of the board of points are the two that can never leave that board.
Stalemate is a draw, as is normal, castling is as in standard Chess, and a Pawn moving two steps on its first move is subject to en passant capture both from another Pawn making a normal Pawn capture, and from one making a half-step Pawn capture.
If one is thinking in terms of elaborate equipment for this game, a board of the design in the middle of the illustration above, but with the squares between the octagons which represent the points on the board being raised platforms might help to assist players in thinking of the game as being played partly on one board with all the spaces, and partly on two different boards on two different levels. Or, to go further yet, one might imagine pieces made of clear plastic, perhaps even hollow shells of clear plastic, so as to appear ghostly, but which, when standing on the octagons, are illuminated from below and thus apparently solidified.
One consequence of being able to move from the squares to the points is that the Bishop can return from the points to a square of the color opposite from the one it left.
The third board at the top can be said to "give the game away", and explain how it is that the Bishop has become able to change color. With the black squares on that board corresponding to the squares of the ordinary chessboard, the Rook becomes a Bishop, and the Knight becomes a Camel. So, as those are two pieces that can never change color, this explains why those two pieces are debarred from the points and must forever remain on the squares.
And this explains how the Bishop gains its ability to change color from its new ability to move to the points. The word Dabbaba means "war machine" in Arabic, and was used as the name for pieces with many different moves in different enlarged versions of Chess. In Timur's Chess, it meant a piece that could only move two spaces orthogonally, and this is also what this name is used for by Fairy Chess problemists, but with the unambiguous stipulation that a Dabbaba ignores intervening pieces on the square one orthogonal step from it when moving.
A piece that can move repeatedly as a Dabbaba in the same direction in one move is called a Dabbaba-Rider, just as a Bishop is a Fers-Rider and a Rook is a Wazir-Rider. A Dabbaba-Rider, like the Dabbaba itself, can only reach one-quarter of the squares on the board.
And the Bishop of the ordinary game of Chess, that is confined to the squares, and not the points, becomes a Dabbaba-Rider on the third board of the diagram. So it can only reach one-quarter of the squares on that board, or one half of the black squares on that board, which correspond to the squares of one color on the regular Chessboard.
But when it gains the power to stop on the points as well, then, on the third board, it changes from a Dabbaba-Rider to a Rook, which can reach every square. Halving the size of the step quadruples the number of spaces that can be reached, and so it is not remarkable, but is to be expected, that the Bishop has gained access to both colors on the regular board in addition to the whole of a second board.
But a Bishop in this game is not quite the same as a Rook on the third board. If it moves from a point to a point, it can only be blocked by intervening pieces on a point. If it moves from a square to a square, it can only be blocked by intervening pieces on a square.
One way to obtain this kind of movement is to think of the Bishop as being a rather unusual kind of combined piece: a piece that can move both as a Rook and as a Dabbaba-Rider. Where the Rook would be blocked, but the Dabbaba-Rider can move, this piece can also go.
However, while this is satisfactory for this type of move, it oversimplifies the real intent of this type of gameboard. The real rule is that diagonal moves of an even number of half steps are deemed to be taking place on either the board of points or the board of lines, with the other board completely ignored, while diagonal moves of an odd number of half steps are deemed to be taking place on the combined board whose real nature is shown in the third of the diagrams above.
A case where this would be relevant is if the array contained a Vao. In Hsiang Ch'i, the Chinese form of the game of Chess, a piece known as the Cannon, or P'ao, moves without capturing like a Rook. To capture, it also moves along Rook lines, but it leaps over one piece, whether a piece on its own side or that of an opponent, to capture the next piece beyond it in the same direction.
Fairy Chess problemists have not only included this piece, called the Pao, as one of the pieces they might include in a problem, but have also added the Vao, which behaves the same way along Bishop lines, and the Leo, which is a combined Pao and Vao, exactly as the Queen is a combined Rook and Bishop. (I have just recently learned that there is also the Nao, which moves in this manner along Nightrider lines.)
The distinction becomes relevant because the intended movement of the Vao on this board is not properly simulated by combining the Pao with what might be called a Dabbaba-Rider-Mover/Dabbaba-Rider-Skipper-Capturer where the term Skipper means a piece that skips over exactly one obstructing piece on its line of movement to any square beyond not further obstructed. I have had to invent a term of my own for this; there is, though, an existing Fairy Chess term, a Hopper, for a piece that skips over one obstructing piece to the next square beyond only.
The reason is that such a combined piece could capture like a Bishop on a move from one square to another if there was a piece on an intervening point it could use as a screen, and this is not how I intend the rules to work: a move that has both its starting point and ending point on the same board, can neither be obstructed nor facilitated by pieces on the other board.
If a Nao is derived from the Nightrider, then perhaps one could have a Zao, derived from the Zebrarider, and a Cao derived from the Camelrider. And perhaps one could even claim the Dabbaba-Rider was important enough to give rise to the Dao. Then, the reason why a combined piece having the moves of both the Dao and the Pao on the third board is not equivalent to the Vao in this game is obvious: "The Dao that can be spoken of is not the true Dao."
Of course, it is not actually the Dao that is the problem with the combined piece, but rather the Pao that has to be replaced with one that can only capture a piece that is an odd number of squares away, but I could hardly let a detail like that stand between me and the opportunity to make an unspeakably vile pun.
Given that the appropriate rule for the behavior of a Vao in Spectral Realm Chess has been given above, the idea behind Spectral Realm Chess could be extended to variants with other pieces.
The rule for the Vao, again, is that a move which starts and ends on a space can only use a piece on a space as a screen, and a move which starts and ends on a point can only use a piece on a point as a screen. Moves between a square and a point (starting on a square and ending on a point, or starting on a point and ending on a square) may use a piece on either a square or a point on the relevant diagonal as a screen.
In a few cases, however, it might be difficult to decide whether or not a piece has the type of diagonal move that would allow it to switch between squares and points or not.
Following the principle that the Pawn can capture by a half-step diagonally, and the King can move a half-step diagonally, pieces with a single-step diagonal move will also be allowed a half-step diagonal move.
Thus, the Fers will also be able to move and capture a half-step diagonally, the Man, with the same move as the King, will be able to move and capture a half-step diagonally, and the same applies to the Counsellor, a combined Knight plus Man.
The Duke, which can move one or two steps diagonally, will be allowed diagonal moves of 1/2 step and 1 1/2 steps as well.
The Archer, a King-mover/Knight-capturer, adds the half-step diagonal move when not capturing; the Sprinter, a Giraffe-mover/King-capturer, adds the half-step diagonal move only when capturing.
Pieces restricted to a diagonal move of exactly two steps, on the other hand, since they cannot take a diagonal move of one step, should not be able to take any additional half-step moves.
Thus, the Alfil, the Star (a combined Wazir plus Alfil), and the Squirrel (a combined Dabbaba plus Knight plus Alfil), would not be able to change from squares to points.
The first step in the move of the Griffin would not be allowed to change to a half step.
As for the Rhinoceros, it might seem reasonable to allow the diagonal steps in its move to be stopped at a half step, but as these half steps would not be followed by a change in direction, on balance it seems better to make the choice to disallow this.
The diagonal move of the Grasshoper raises an interesting question. If a Grasshoper begins its move on a space, and passes over a screen on a point, should the next space beyond, where it lands, be a full step further, or, since this move is made in terms of a board including both the squares and points, only a half step further? Since, in the latter case, the move would begin and end on a square, making the screen invisible if the precedent of the Vao is applied, it seems the reasonable decision is to have the next space, where it lands, be a full step further, on the same board as the screen.
Promotion of a Pawn on the last rank of the board of points would be to any piece in the initial array that does not have the ability to switch boards.