Four more APL operators are illustrated here:

Here, we meet compress, expand, take, and drop.
Compress lets us form a shorter vector from selected elements of an input vector. Expand lets us fill a longer vector with the elements of an input vector.
Take selects the first few elements of a vector, or the last few with a negative first argument. Drop instead omits the first few, or the last few, elements of a vector.
Compress and expand can also act on a selected dimension of a matrix.
This will be illustrated below for the compress operator.

A three-dimensional array with 24 elements is created by the first statement shown, and placed in W. Then, we print W, so that it is possible to clearly see what is happening here.
Using the compress operator in its normal form, compression takes place along the last dimension of the array. Therefore, the compression vector has to have four elements.
If it is desired to perform compression along the second dimension, this is specified explicitly by using 2 as a subscript to the operator. In that case, the compression vector has three elements.
Finally, a special form of the operator, with the minus sign as an overstrike, indicates compression takes place along the first dimension of the array. For the array W, the compression vector then has two elements.
The unary reverse operator, and the dyadic rotate operator, which we have not yet met, also have the ability to apply along a selected dimension.
Here, we see outer product.
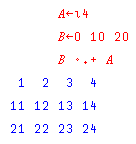
This allows an operator to be modified so that it can act on a pair of vectors and form a table, as illustrated at the left. It can also act on arguments other than vectors, producing multi-dimensional results.