
APL, which stands for A Programming Language, had its roots in a notation for algorithms devised by Kenneth E. Iverson. This notation, however, differed in several important respects from the APL computer language we are familiar with today. All the implementations of APL of which I am aware derive from the version of the language used in the IBM program product APL/360.
One of the most distinctive features of APL is that it uses a special character set. Thus, an APL keyboard may look like this:

This is a 44-key typewriter keyboard. The terminal originally used with APL was an IBM 2741, which was a KSR (keyboard send-receive) printing terminal based on the IBM Selectric typewriter. The printing element on this terminal could, therefore, be freely interchanged, and it was the famous "golfball" element with 88 characters.

For use with APL, stickers were applied to the front of the keys.

There were numerous other devices with APL keyboards of one type or another. The IBM 5100 portable computer offered APL as one of the two languages available for it, and thus had an APL keyboard:
IBM also offered a version of their 3277 terminal which had an APL character set; this was actually the least expensive way to get a 3277 which had lower-case support as well.

APL/360 provided timesharing capability to IBM System/360 computers without requiring them to have Dynamic Address Translation hardware, as was only offered on the Model 67, or a time-sharing operating system such as TSS or TSO running on OS/360. This was possible as users could only run interpreted programs in the APL language, not programs written in assembly language, or programs written in FORTRAN and compiled.
Thus, the APL/360 program was an applications program that was connected to a number of terminals, and which shared time between them in software. This method of providing time-sharing in an interpretive language environment without the need for a full time-sharing operating system had been used before, particularly with the computer language BASIC, but also with modified versions of FORTRAN.
Computers from Burroughs, Control Data, and DEC also offered APL interpreters, and people attached ASCII terminals to IBM mainframes as well, either in order to save money because suitable ASCII terminals were available more cheaply, or to allow the same terminal to be used with an IBM mainframe and a local minicomputer.
The original terminal used for APL was the IBM 2741 printing terminal, which was based on the Selectric typewriter mechanism. This made it easy and natural to generate the additional overstruck characters used in APL by backspacing and then typing the remaining component of the character.
In the case of the 3277 keyboard above, note how all the overstruck APL characters used with APL\360 are explicitly placed on the keys, to be typed by means of the extra APL ALT shift key.
This, of course, required special software support. Thus, the most common APL terminals from other companies were printing terminals, whether they also used a Selectric mechanism, or a dot-matrix printhead, or a daisywheel. Tektronix also provided an APL keyboard and character set for its storage tube graphics terminals, since with such terminals, overstrikes could be performed in much the same way as on a printing terminal.
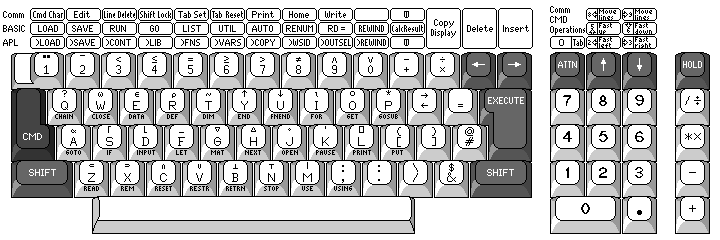
There were other CRT terminals that supported APL also. For example, Hewlett-Packard made their 2641 intelligent terminal, the keyboard of which is shown below:
Here, unlike the 3277 from IBM, overstruck characters are not shown explicitly on the keys, so they are entered by backspacing. However, like the 3277, this terminal included the possible overstruck characters it could display as individual entries in its character ROM. The HP 2641 supported not only the overstrikes used in APL\360, and those used on Hewlett-Packard's own dialect of APL for the HP 3000 minicomputer, but also a wide selection of overstrikes found on other versions of APL in use at the time.
The HP 264x line of terminals were intelligent terminals; they had 8008 microprocessors, or in one case an 8080 microprocessor, to allow them to handle complex functions. If the terminal itself turned overstrikes into one of the available overstruck characters where possible, it could have avoided the need for the host computer to directly support its specific internal character set, allowing it to be treated, at least in that respect, like a printing terminal. However, they were block mode terminals, so they still needed some specialized software support.
A Montreal company, Lektromedia, made an ASCII video terminal that had two planes of text memory and two character generation circuits, with an OR between them, so that it could allow a fully general overstrike capability. Naturally, a keyboard with APL characters and the ability to switch between the ASCII character set and the APL character set was offered as an option with that terminal. This allowed the terminal to be treated in the same way as a printing terminal, instead of requiring special software support, based on the specific repertoire of overstruck characters the terminal offered. But video displa terminals with this kind of capability were relatively uncommon.
Two keyboard arrangements for ASCII terminals with APL capability became popular, to allow the APL characters to take their usual positions on the keyboard for the two most common keyboard arrangements:
the typewriter-pairing version of APL/ASCII, and

the bit-pairing version of APL/ASCII.
APL is also not the first computer language to attempt to provide an approach to more natural mathematical notation through the use of a special character set, or even the first language to use overstruck characters. The language COLASL, used on the STRETCH computer at Los Alamos, used a special terminal device which allowed the use of a large character set. The letters of the alphabet could be overstruck with squares, circles, or several other symbols to increase the number of available variables.
Originally, it was envisaged that, in addition to using the underline character to increase the number of letters for forming variable names, that the box character could enclose a letter, and the diaresis (two dots) could appear above the letter. Since in APL, as in most other conventional computer languages, a variable name could be a word of several letters, not just a single letter (following mathematical notation, as done in languages such as COLASL, MADCAP, MIRFAC, and the Klerer-May System) presumably no need for this was seen.
Interestingly enough, one way in which COLASL could have influenced APL, as, while the language itself was developed at Los Alamos, IBM provided them with the 9210 Scientific Descriptive Printer, used to prepare punched cards for the input of COLASL programs, is that in the printed form of a COLASL program, the digits from 0 to 9 were, to make them more distinctive from letters (both upper and lower-case were available for preparing COLASL programs) of a reduced height, and italicized. This could have helped to inspire the use of italic letters with APL/360 later.
Incidentally, the arrangement used for the APL keyboard resembled that used for CALL/360 BASIC:

The degree symbol was the shift of J, where the null symbol was in APL; the equals sign, used for assignment in BASIC, was where the left arrow was in APL, and the parentheses were on the same keys as in APL, but as unshifted characters. As well, the up-arrow, used for exponentiation in BASIC, was on the same key as the power symbol in APL, and the symbols used for the four basic arithmetic operators were in the same place as well.
However, APL/360 predated CALL/360 BASIC; as the CALL/360 service also offered APL, it was no doubt decided to use a keyboard arrangement that would reduce confusion for customers using both languages.
But what was unique about APL was that it not only allowed arrays and matrices to be directly manipulated, but that it provided a very powerful set of primitive operations for this.
Let us now begin an introduction to APL.
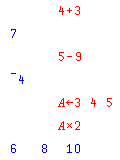
On the left, we see a transcript of a small portion of a hypothetical APL terminal session. For clarity, what is typed by the user is in red, and what is typed by the computer is in blue.
In APL, the interpreter doesn't print a prompt character on the paper to indicate that it is requesting input, it simply indents six spaces. If an expression is typed, the interpreter responds by printing its value.
Our first example input illustrates addition. The user asks for 4 plus 3, and the computer correctly replies with 7.
Our second example illustrates a subtraction calculation which produces a negative number as a result. Why does (or, rather, why did the earliest implementations of) APL use italic letters, instead of something more natural and useful? The answer was so that it would be easy, by sight, to tell the letter O from the numeral 0. Unlike some old typewriter keyboards, computer keyboards always distinguish the numeral 1 from the (lowercase) letter l and the (uppercase) letter I. In APL, there is also a different character for the minus sign and the subtraction operator.
Our third example does nothing, it appears. But that is because the arrow pointing left is an assignment operator. A value is being stored in the variable A. That lets us use A as an element in subsequent calculations.
But, wait a moment. What kind of an expression is three numbers, with spaces between them?
The answer is that it is a vector-valued constant. As we see in the next line. We multiply A by two, and the answer is a row of three numbers, each one twice the corresponding number in A. This illustrates one of the important aspects of the power of APL. A variable can contain an array of numbers, and operations act on entire arrays, not just on individual values.
Let us continue.
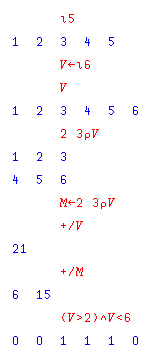
Since the power of APL lies largely in its ability to handle vectors automatically, many of our examples will use vectors. So, one of the first functions we will look at in APL that is related to vectors is one that lets us create vectors without typing out each element in a vector.
Thus, we see that the Greek letter iota is used as an operator which, when applied to n, creates the first n integers in order.
We assign a vector of the numbers from 1 to 6 to V, and then check that V is what we expected.
Our fourth example command uses another Greek letter, the letter rho. This is the restructure function, and turns our 6-element vector into a 2 by 3 matrix. After seeing this in action, we assign this matrix to M.
Now we see what the forward slash is used for in APL. The traditional division symbol is used for division; the forward slash is used for a powerful function that builds a new function from an operator. The sum of the elements of V is what it produces in this example, which is 21.
When we apply it to a matrix, the result will be a vector, the operation being performed over the last dimension of the matrix.
Our final example is a simpler one; we use the relational and logical operators on our vector V to produce a vector containing zeroes except when the corresponding element of V is both greater than 2 and less than 6. Note the placement of parentheses; this illustrates that in APL, the order of evaluation is strictly from right to left. A simple rule such as that is needed in a language like APL with a large number of operators, and this particular rule works best with a conventional right-to-left assignment operator.
Of course, this language is a programming language. Thus, the next thing we should see is how to write programs in it.

By starting a line with the upside-down triangle symbol, we begin a function definition. Until the end of the function definition is signalled by another such symbol, we will be prompted with a line number from now on.
The function header begins the function. Here, the function returns no result, and is a unary operator, having only one argument on the right.
The semicolons after the function prototype separate the local variables to be used within the function.
This function solves the quadratic equation. The three coefficients in the polynomial are given in a vector, so we begin by removing these components from the vector, and assigning them to three simple values.
Then, we calculate the discriminant, b squared minus 4ac.
Statement 5 is a three-way branch. The unary multiply is the signum function, and so it returns -1, 0, or 1, depending on whether the discriminant is negative, zero, or positive. Statement labels are the numbers of the lines they are on; the comma concatenates them into an array, and two plus the signum forms the index into the array. The result, the line to branch to, is given to the right arrow, which is the APL branch operator.
Statement 6 is a comment line. Its first character is not found on the APL keyboard, because it is an overstrike, formed by backspacing so that the intersection and null characters are printed on top of each other.
Statement 7 begins with a statement label. NEG is a variable containing the value 7; if the function is edited, NEG will contain the number of whatever line it is on, facilitating its use as a branch target. A string constant is what the line consits of, and thus, that value will be printed when the line is executed; thus, the program announces that we have two complex roots when the discriminant is negative.
In statement 9, we meet the star, which, in APL, is an exponentiation operator.
In statement 10, we see that the semicolon is used to allow printing numbers and character strings on the same line.
Line 12 is a branch to statement 0; this is a program exit.
It may be noted that this example program could be cited almost as an example of how not to program in APL. The fact that it uses branching, as well as the way it treats its input argument, limits it to arguments in only one form, a three-element vector. Thus, the power of APL arguments to act on arrays of any size is not used by this function. For some problems, that is necessary. For others, branching would still be used, but at a high level of the program, with flexible array operations still taking place within it.
Only a small amount of APL has been illustrated here. Hopefully, it is enough to give a brief idea of the language; there are many resources on APL available on the web.
However, this site continues on for those who would wish to delve more deeply into the subject before leaving this site.
Before IBM created the APL keyboard, for the Los Alamos Scientific Laboratory IBM created, for use with the STRETCH computer from IBM that they had purchased, the 9210 Scientific Descriptive Printer, which also had an unusual keyboard with a lot of mathematical symbols on it. It was a keypunch rather than an interactive printing terminal, but it also included a typewriter; since it was designed to prepare punched cards containing programs in the programming language COLASL, and that language used mathematical expressions in a two-dimensional notation, each line of the program could correspond to up to three punched cards. Thus, instead of producing interpreted cards, a copy of the program was typed at the same time the cards were punched to allow the operator to keep track of the program being enetered.
Like APL, it even used italics to distinguish between letters and digits, although in its case it was the digits that were italicized.
Its keyboard looked like this:
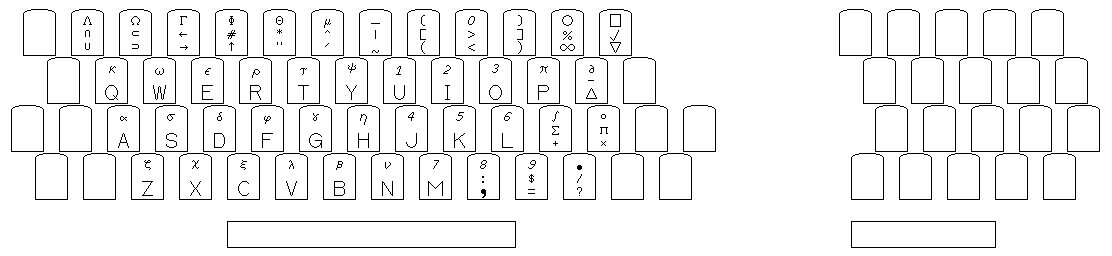
The digits are arranged in the style of a numeric keypad because the 9210, although it also produced a record of what was typed on it on paper like a printing terminal, was a keypunch, and this was how the keyboards of keypunch machines were laid out.
Despite COLASL being used in batch mode, it did use overstruck characters like APL would later come to do. In APL, letters in variable names could be underlined; in COLASL, they could be enclosed in either a circle or a square, and there were also sixteen symbols that could be placed above a letter, and a letter could both be enclosed and surmounted by one of those symbols at the same time. This made up for the fact that variable names could only be one letter long in COLASL (so ab was a times b, just as in mathematical notation).
The sixteen symbols placed above variable names were actually printed on the line above in program listings; they were full sized symbols also used as punctuation marks or arithmetic operators, not symbols that were small and raised to be overstruck like accent marks. A line of COLASL code was normally punched into a set of three cards, with the first one containing superscripts and the third subscripts.
However, the most distinguishing feature of COLASL was that comments could be put in programs anywhere by shifting them to be printed in red, and so some COLASL programs looked like prose descriptions of their algorithms.
As another incidental curiosity, the APL supplied workspace 10 PLOT contained APL programs to draw simple graphs out of printed characters. A workspace which allowed plots with finer resolution to be printed on the 2741 was 10 FINEPLOT. It had improved versions of the plotting programs, which required the use of a special element for the 2741 terminal (the elements being like those for the Selectric typewriter). Here is a chart of the layout of that element:
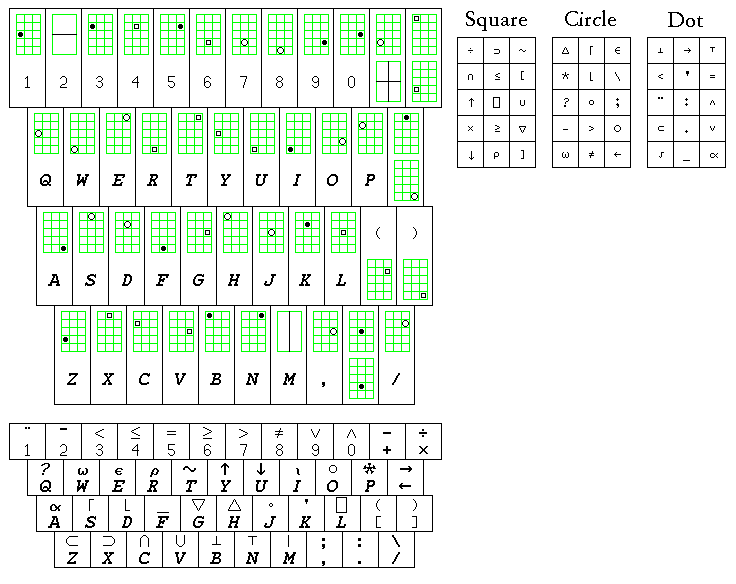
There were three plotting symbols, a square, a circle, and a dot. With fifteen copies of each symbol on the typing element, in three possible positions across, and five possible positions vertically, the terminal, printing as would a 10 pitch typewriter, with the conventional six lines per inch, could position the symbols with a resolution of 1/30 of an inch in both directions.