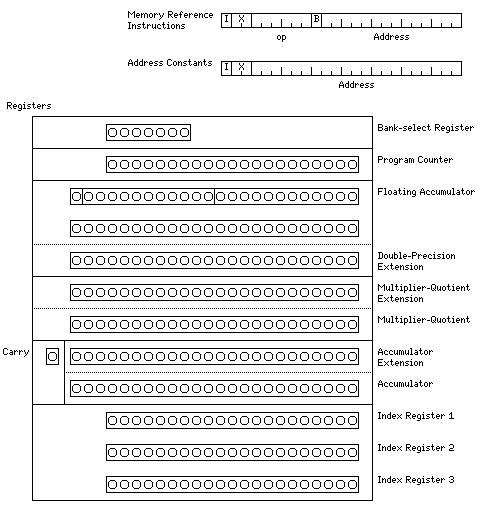
The diagram below summarizes what the architecture of a machine which both had a 24-bit word length and which had the type of simple design which that word length makes possible might look like:

Memory-reference instructions contain one fourteen-bit address which points to a location in a memory consisting of 16,384 words, each 24 bits long. In the old days of computers, such a memory was considered quite large, and even if an architecture provided for such an address space, that much memory would be optional; the basic complement of memory might have been more like 4,096 or 8,192 words of core memory.
The instructions have no register field; instead, the computer would simply have a single accumulator corresponding to each type of operand it worked with. Thus, the computer would have a 24-bit accumulator for integer arithmetic, and a 48-bit floating-point accumulator, allowing for floating-point calculations with 10-digit precision, comparable to that provided by a pocket calculator, and thus significantly higher than the basic floating-point precision of 32-bit or 36-bit computers.
The floating-point accumulator would have a 24-bit extension for double-precision numbers with 18-digit precision. And a multiplier-quotient register would be associated with the accumulator to allow integer multiplication to produce a double-width result, and so that the accumulator could retain the remainder after division. Also, the accumulator would have a carry bit associated with it.
As well, since 24-bit integers are not long enough for all purposes, both the multiplier-quotient register and the accumulator could be extended to 48 bits.
In the instruction format, the first bit would indicate indirect addressing, and the second and third bits would either be zero, to indicate indexing was not taking place, or, if nonzero, would identify an index register. So, the computer would have three index registers; having more than one index register is useful to permit operations involving multiple arrays.
Since a full 24-bit address, allowing the use of 16,777,216 words of memory, would have seemed impossibly visionary in the early days of computers, addresses stored in memory would also include the bits for indirect addressing and indexing, allowing chains of indirection.
But since an address constant in memory doesn't need an opcode, not being an instruction, allowing the other 21 bits of a word in memory to serve in an address, instead of just the last 14, so that a computer could have multiple 16,384-word memory banks attached, would have suggested itself. And so the bit following the opcode in an instruction would be used for bank selection; if that bit is a one, instead of the current memory bank being used, instructions would reference memory in the memory bank indicated by the bank-select register.
Unlike a 12-bit or 16-bit computer, which would have to use small memory pages containing from 128 to 512 locations, the 14-bit address in an instruction is large enough that it could be envisaged as a complete address in normal operation, and the bank select feature would simply be an exotic feature used for work on very large problems; or, when memory became cheaper, the computer might use a separate memory bank for each user of the computer in a time-sharing mode.
The instructions would usually involve retrieving a number from the word indicated by the address part, and performing an arithmetic operation with the contents of the accumulator as the first operand, and the number fetched from memory as the second, storing the result in the accumulator.
But there would be various modifications to that theme.
The store instruction would instead take the number in the accumulator, and put it in the memory location pointed to by the address.
Some instructions would work with two or three words in memory, and use a different register, instead of the accumulator. The floating-point instructions would be examples of that. There would also be instructions to load and store the multiplier-quotient register and the index register.
And then there would be the jump instruction, which would point to the address from which the program would continue. There would also be a jump to subroutine instruction of some type, which would be more complicated, as it would save a return address somewhere; the index register might be one possibility.
Also, there would be other instructions which simply modified the contents of the accumulator, with the individual bits in the address field guiding the operation.
The instruction set for this example computer could look like this:
00 EMA Exchange Memory and Accumulator 01 CAS Compare and Skip 02 LDA Load Accumulator 03 STA Store Accumulator 04 ADD Add 05 SUB Subtract 06 MUL Multiply 07 DIV Divide 10 AND And 11 ORA Or with Accumulator 12 XOR Exclusive Or 17 DVX Divide Extensibly 20 LEM Long Exchange with Memory 21 LCS Long Compare and Skip 22 LLD Long Load 23 LST Long Store 24 LAD Long Add 25 LSB Long Subtract 26 LMP Long Multiply 27 LDV Long Divide 30 LAN Long And 31 LOR Long Or 32 LXR Long Exclusive Or 37 LDX Long Divide Extensibly 40 FEM Floating Exchange with Memory 41 FCS Floating Compare and Skip 42 FLD Floating Load 43 FST Floating Store 44 FAD Floating Add 45 FSB Floating Subtract 46 FMP Floating Multiply 47 FDV Floating Divide 50 DEM Double Exchange with Memory 51 DCS Double Compare and Skip 52 DLD Double Load 53 DST Double Store 54 DAD Double Add 55 DSB Double Subtract 56 DMP Double Multiply 57 DDV Double Divide 62 LDX Load Index 63 STX Store Index 64 JMP Jump 65 JSR Jump to Subroutine
for the memory-reference instructions. The index field in the load and store index instructions would indicate which index register is the destination of the instruction, instead of indicating indexing (this trick actually was used in some real computers). Subroutines would begin with an address, and the return address would be stored at the location pointed to by that address: thus, the action of the jump to subroutine instruction would be to store the address of the instruction following it where the address at its destination points, and then branch to the location following its destination.
Opcode 70 would be used for the shift instructions, opcode 71 for the operate instructions, and opcode 76 for input-output instructions.
Integers are represented, as illustrated above, in binary notation. Instead of dealing with integers from 0 to 16,777,215, however, the computer also deals with negative numbers, and uses two's complement notation to do so.
The example architecture above is not very different from some real 24-bit architectures, having a layout of its instruction word very similar to that of the SDS 9300 and the DDP-224.
However, most of the classic 24-bit machines, instead of using the conventional type of floating-point format illustrated here, treated floating-point numbers as consisting of a signed mantissa followed by a signed exponent. They combined this with treating fixed-point numbers as fractions rather than integers; this increased the efficiency of simulating floating-point operations on machines without hardware floating-point but with hardware multiply. Some of those machines skipped a bit in the second word of a two-word integer so that there was no need for a corrective shift when fixed-point numbers intended to be interpreted as integers were multiplied.