This page deals with methods used to record data on reels of magnetic tape, some of which are also applicable to floppy disks or hard disks.
IBM set many of the standards for magnetic tapes during much of the computer era, defining 7-track tape and 9-track tape. UNIVAC computers used an 8-track tape format in a few cases, and the Digital Equipment Corporation provided small spools of tape in a unique format, DECtape, which allowed spools of tape to function as random-access storage devices much like floppy disks.
The layout of tracks on a 7-track tape was:
C (parity) B (32) A (16) 8 4 2 1
These tapes were recorded using NRZI, whether 200, 556, or 800 bpi; in fact, NRZI was also used for the 100 bpi tapes used only with the first IBM reel-to-reel vacuum-column tape drive, the IBM 726, used with the IBM 701 computer; these tapes were also 7-track tapes, and had the same layout as later 7-track tapes, although they used odd parity, with even parity being the general convention for later 7-track tapes. Both Raytheon and Univac did record computer data on magnetic tapes shortly before IBM, but it was the performance that the IBM invention of the vacuum column made possible that revolutionized the industry.
While it wouldn't matter with later, more advanced modulation methods such as Phase Encoding (PE) or Group Code Recording (GCR) to be discussed below, with NRZI, using even parity came with an obvious penalty: an all-zero character would have a zero bit, and thus there would be no timing pulses produced from reading the moving tape, and all-zero characters would look like areas of tape on which there was no recording.
In the code used by IBM for writing data on seven-track tapes, the space character corresponded to the all-zero code, so this was a serious issue. It was dealt with by including a character called "substitute blank" in BCDIC, to which spaces were translated before writing text on a tape.
Because the characters were written on tape with modified zone bits, the all-zeroes character that was so substituted wasn't the space character, but instead the digit zero.
Why use even parity, and create such a problem?
After thinking about the matter, I realized what the reason was: with odd parity, codes like 1000000, 0100000, and 0000001 would all be valid. So a single bit error would turn those codes into an all-zero code.
But treating an all-zero code like an error, as something that should never occur on a tape, isn't appropriate: normally, tapes will consist of records of data with stretches of blank tape between them.
Tapes can, however, be "blocked" instead of "unblocked", so that they consist of very long records of uniform size, so that the overhead of blank space is minimized; then the block format contains fields which indicate where the actual records of the data begin and end.
So even parity allows parity to work as intended - every valid character that should occur on a tape is at least two bits different from every other valid character, including the all-zeroes blank stretches of tape.
This is fine if one only records text on a tape. But what if one wants to save space by recording binary data on the tape?
One way to allow the use of odd parity would simply be to begin and end every record with a special character that is quite distinct from the all-zeroes character. That divides the tape into areas which don't include blank space, and areas which only contain blank space, so the fact that odd parity doesn't quite fully distinguish between data and blank space stops being a problem.
Another reason for using even parity for tapes containing character data, so that measures like that could be avoided, was to simplify the design of auxilliary equipment that used tapes, specifically, off-line devices that recorded data from punched cards on to magnetic tapes, or which punched cards with data read from magnetic tapes.
At least on the earliest 9-track tapes, the ones recorded at 800 bpi, the tracks were as follows:
4 (8) 6 (2) 0 (128) 1 (64) 2 (32) P (parity) 3 (16) 7 (1) 5 (4)
The numbers for the tracks, and the ordering of the tracks was that given by IBM in early documentation; later references to how 9-track tapes were written quoted an ANSI standard which reversed both the order of the tracks and the bit numbering convention, so that the ordering was termed:
2 0 4 P 5 6 7 1 3
in many references.
Some sources have indicated that on tapes recorded at 6250 bpi, however, the order of tracks was:
1 4 7 P 3 6 0 2 5
but this could have been simply another variation in expressing the order, as the manuals for the Kennedy 9400 TriDensity tape drive and the Pertec T1940-96 tape drive both clearly give the track order of the 6250 bpi format as being the same as that for 1600 and 800 bpi. When tape having the capability of recording at 6400 fci first became available, shortly before IBM developed its 6250 bpi format with GCR, some independent manufacturers simply recorded on such tape using phase encoding but at double density; occasionally, this was referred to as DPE recording, but it was not a different modulation method. Although several manufacturers provided tape drives operating at that density, and an ANSI standard for such tapes was formulated, as IBM tape drives did not support that format, and as IBM's GCR format, which recorded almost twice as much on the same tapes, was available for licensing, it never became popular.
Or, rather, almost the same tapes. Just considering the overhead of GCR, a tape would have to be capable of about 7820 fci to support 6250 bpi, and, in fact, a 6250 bpi tape in the IBM format which included GCR actually had to support 9042 fci: for one thing, a longitudinal parity byte was included after every seven bytes of data. Neglecting any overhead other than GCR, a tape rated for 6400 fci could contain data at 5120 bpi.
The layout of tracks on DECtape, which had ten tracks, was as follows:
T M 1 (4) 2 (2) 3 (1) 1 (4) 2 (2) 3 (1) M T
The timing track had a transition in the middle of each bit area, and the mark track usually had alternating groups of three ones and three zeroes. Since LINCtape, the ancestor of DECtape, originated when half-inch wide tape still only had seven tracks on it, rather than nine, both were on 3/4" wide tape.
LINCtape was recorded using phase encoding at 420 bpi.
The mark track contained four-bit codes indicating the type of the 12 bits of data repeated on the three data tracks.
These codes were:
0000 indicated the beginning and end of tape
1111 (repeated 5 times) provided a gap between blocks
1110 indicated the copy of the block number at the start of the block
0010 indicated one unused word, to protect the block number
from being disturbed when the main portion of the block
containing data was re-written
1001 (repeated 255 times) indicated data words
1011 indicated the last word of data in a block
0001 (repeated 3 times) indicated a three-word area containing
a checksum for the block in the first word, followed by
two unused words
0111 indicated the copy of the block number at the end of the block
The order in which the 12 bits of a word of data were placed on the three data channels of the tape was as follows, where the bits are numbered using the convention MSB 0 ... 11 LSB:
1) 0 3 6 9 2) 1 4 7 10 3) 2 5 8 11
DECtape was recorded using phase encoding at 375 bpi.
In this format, whether the DECtape unit was connected to a PDP-4, PDP-7, PDP-9 or PDP-15 with an 18-bit word, a PDP-6 or PDP-10 with a 36-bit word, a PDP-5 or PDP-8 with a 12-bit word, the codes in the mark track were 6 bits long.
The codes in the mark track were chosen to be symmetrical, so that if one both complemented the bits in any code, and reversed the order of the bits, one obtained the code used in the corresponding position at the other end of the block. This meant that bidirectional reading and writing of blocks, a feature not provided with LINCtape units (although searching for a block with a given number was bidirectional) could be offered with very little additional circuitry.
The codes used with DECtape were:
010010 marks the beginning of the tape
010110 marks the block number at the start of the block
011010 indicates blank space to protect the block number
001000 (repeated four times) indicates first another unused
word, then the reverse checksum, and then the first two
words of data in the block
111000 indicates all the words of data in the block except the first
two and last two
111011 (repeated four times) indicates the last two words of
data in the block, then the checksum, and then an unused word
101001 indicates blank space to protect the block number
100101 marks the block number at the end of the block
Since the block numbers were part of the format of the tape, no space was added between the block number at the end of one block and the block number at the start of the next block.
The block number at the end of the block was recorded so that it would be reflected along the motion of the tape to be readable in the same way when the tape was searched in reverse.
Although much of the format of DECtape was the same for each type of computer to which DECtape units were connected, the order in which data bits were placed on the tape varied depending on the type of computer used.
For the 18-bit computers, the PDP-4, PDP-7, PDP-9, and PDP-15, two arrangements were used.
With the original Type 550 controller, the data bits were put on the tracks like this:
1) 5 4 3 2 1 0 2) 11 10 9 8 7 6 3) 17 16 15 14 13 12
but with later controllers, such as the TC15, the data bits were in this order:
1) 0 3 6 9 12 15 2) 1 4 7 10 13 16 3) 2 5 8 11 14 17
For the 36-bit computers, the PDP-6 and PDP-10, it was:
1) 0 3 6 9 12 15 18 21 24 27 30 33 2) 1 4 7 10 13 16 19 22 24 28 31 34 3) 2 5 8 11 14 17 20 23 26 29 32 35
and for the 12-bit PDP-5 and PDP-8, two arrangements were also used.
With the original Type 552 controller, the data bits were put on the tracks like this:
1) 2 5 8 11 2) 1 4 7 10 3) 0 3 6 9
but with later controllers, such as the TC01, the data bits were in this order:
1) 0 3 6 9 2) 1 4 7 10 3) 2 5 8 11
Thus, initially, the Type 550, 551, and 552 controllers each used a different direction for recording data for the 18, 36, and 12 bit word architectures respectively, later DECtape controllers standardized on the orientation used with the 36 bit machines.
DECtape drives were also connected to PDP-11 computers, and they used the same data format as later 18-bit interfaces, ignoring the first two bits of each word:
1) X 14 11 8 5 2 2) X 13 10 7 4 1 3) 15 12 9 6 3 0
using the MSB 17 ... 0 LSB convention of the PDP-11. The controller could read the unused bits with special instructions for reading tapes made by other systems.
While recording three words in a 48-bit block would be possible, three such blocks would need to be treated as a unit to remain synchronized with the mark track codes (just as PDP-8 12-bit words were handled in groups of three) and this is likely why that alternative was avoided.
It was possible, both with DECtape and LINCtape, to use a different number of words (18 bits long and 12 bits long respectively) per block than 256; this was normally considered nonstandard, but with the PDP-8, the normal format was to use 86 18-bit words per block (and therefore 129 12-bit words).
Although it did not attempt to provide random access to blocks on the tape, the KDF9 computer also used 3/4" wide tape with duplication of tracks. The KDF9 computer used sixteen-track tape (of a format previously used with another English Electric computer, the KDP10). Two sets of eight tracks, containing one timing track, one parity track, and six data tracks, were present, the same character being duplicated in the two sets of tracks.
(parity) (32) (16) (timing) (8) (4) (2) (1) (parity) (32) (16) (timing) (8) (4) (2) (1)
These tape drives look the same as those used on the RCA 501 computer, and an advertising brochure for that computer noted that all data was recorded twice on its tapes as well.
Actually, that should not at all be surprising - the aforementioned KDP 10 was, in fact, an RCA 501 manufactured by English Electric under licence from RCA. But the RCA 501 manual gives the sequence of tracks as slightly different on that computer (and presumably on the KDP 10 as well) from that given for the KDF 9:
(parity) (32) (16) (8) (timing) (4) (2) (1) (parity) (32) (16) (8) (timing) (4) (2) (1)
Possibly my source for the KDF 9 had a misprint, as such a deliberate incompatibility seems odd.
The Bendix G-20 computer also duplicated bits on the tracks of its magnetic tape, which was one inch wide.
(block) (parity) (block) (parity) (128) (64) (128) (64) (32) (16) (32) (16) (8) (4) (8) (4) (2) (1) (2) (1)
The tape drives on the Bendix G-20 were very interesting for another reason. They were the model 960 II tape drive from the Potter Instrument Corporation, first made available in 1961, which had a density of 1500 bpi through the use of phase encoding.
However, if it was necessary for purposes of reliability to repeat each bit twice across a tape that was one inch wide, then the areal density of bits was actually less than that of 9-track 800 bpi 1/2" tape. While 9-track tapes, both 800 bpi and 1600 bpi, were introduced by IBM in 1964, along with the System/360, IBM made the IBM 729 tape drive, a 7-track drive with an 800 bpi density, before this - so, while this tape drive marks an earlier use of phase encoding, the density achieved was not unprecedented at the time.
An even wider tape was used by the Honeywell DATAmatic 1000 computer. It used large reels of 3-inch-wide video recording tape, with 36 tracks across the width of a tape. Each tape block consisted of two 48-bit words, each containing eight 6-bit characters, recorded serially on each of the tracks, for a total of 576 characters per block. Blocks were recorded with a gap between them slightly larger than the size of a block, but when the end of a reel was reached, blocks recorded with the tape moving in reverse then filled those gaps.
The tape for the original Univac I computer had eight tracks, and was apparently recorded in the technique I illustrate below as Return to Zero. Some other sources use the term "Return to Zero" for the recording method I note as Bipolar Return to Zero.
1 (parity) 2 (32) 3 (16) 4 (8) S (timing) 5 (4) 6 (2) 7 (1)
Although it used odd parity, it kept things simple through the use of a timing track as well.
Much later, an eight track tape with a timing track was also used with the Navy Tactical Data System, manufactured by Univac and based on their 490 computer. For this tape format, alternate tracks were offset, somewhat simplifying certain aspects of the construction of the read/write heads. Apparently, although the Univac 490 used only conventional magnetic tapes, this tape format was also used with the Univac File Computer in the civilian sector, and the nominal tape density was 139 bpi.
(16) (4) (parity) (timing) (2) (1) (8) (32)
IBM devised a very advanced magnetic tape unit for the National Security Agency which bore the codename TRACTOR. It later attempted to bring this technology to the computing public under the name Hypertape. This used tape cassettes which contained both the supply reel and the take-up reel; the tapes were one inch wide. Sadly, only three customers, one of which was Boeing, the other two being the Internal Revenue Service of the United States and the Department of National Revenue in Canada, opted to install this new advanced tape format. Canada's Department of National Revenue purchased the original model, with a recording density of 1511 bpi on each track, and the other two customers purchased a later model, offered after the introduction of the IBM System/360, which could record at 3022 bpi.
The tapes had 10 tracks, two parity tracks and eight data tracks. The two data tracks corresponding to the two most significant bits of each byte would have been simply left unused when Hypertape was used with a computer, such as the IBM 7090, with six-bit characters. With a computer like the IBM 7074, which worked with decimal digits, two digits were encoded in the data tracks for each column. Data was recorded using Phase Encoding, as was later used with standard 1600 bpi tapes.
C1 P = = C2 = = P I0 8 (128) * . * I1 4 (64) * . . I2 B 2 (32) . . * I3 A 1 (16) * . * I4 8 8 * . . I5 4 4 . . * I6 2 2 * . * I7 1 1 * . .
The function of the two check bits is shown by the asterisks in the two columns to the right. Check bit 1 gave the parity of information bits 0, 1, 3, 4, 6, and 7; check bit 2 gave the parity of information bits 0, 2, 3, 5, and 6.
The intent of this scheme was to make it possible to distinguish errors in adjacent tracks.
Single-bit errors could be divided into three groups.
An error in C1, or I1, I4, or I7 would lead to wrong parity in C1 alone.
An error in C2, or I2, or I5 would lead to wrong parity in C2 alone.
An error in I0, I3, or I6 would lead to wrong parity in both C1 and C2.
In order to allow the Hypertape system to provide error correction, the information obtained from the check bits was combined with information about the analog characteristics of the tracks. A track with a low signal level was considered to be a track which was the most likely to be in error. Since conditions that could potentially cause an error were likely to affect adjacent tracks, the two check bits were defined to permit fine discrimination between adjacent tracks.
The TRACTOR system, used with the 7950 or HARVEST system, likely used NRZI recording, as the decision to use PE was made during the process of designing Hypertape. It used tape that was 1 3/4" wide, and there were 22 tracks on the tape, 16 for data, and 6 check bits, the number required for a Hamming code plus parity. Apparently, no timing track was used, although before the decision to use PE in Hypertape was made, a timing track was envisaged initially for that format. It provided 2400 bpi recording, at a time when 556 bpi was the civilian standard.
It may also be noted that many modern cartridge tapes, even when they have multiple tracks, record the bits of a byte serially along a track. Although IBM did not produce special magnetic tape drives for the STRETCH computer, initially, they envisaged doing so, and they considered a design using this principle to provide an enhanced performance tape drive for it.
After 6,250 bpi reel-to-reel tape, the next major magnetic tape format was that used in the IBM 3480 tape drive. Here, the tracks were:
I0 I7 I1 I8 I2 I9 I3 I10 I4 I11 I5 I12 I6 I13 D1 D2 P1 P2
There were fourteen information tracks; bytes were written along the tracks using a code in which 9 bits represented 8 bits of data, with a limitation similar to that of GCR; while there could be consecutive ones, no two ones could be separated by more than three zeroes, prior to NRZI recording of the coded bits.
The two parity tracks gave parity of half the tape, and the two diagonal parity tracks gave diagonal parity, although the nature of the parity checks would be made more obvious by a re-ordering of the tracks:
P1 P = = = = = = = = = = = = = = = = = = = D1 * = = = * = = = = = = = = = = = = = = P I0 * . . . . * . . . . . . . . . . . . * . I1 * . . . . . * . . . . . . . . . . * . . I2 * . . . . . . * . . . . . . . . * . . . I3 * . . . . . . . * . . . . . . * . . . . I4 * . . . . . . . . * . . . . * . . . . . I5 * . . . . . . . . . * . . * . . . . . . I6 * . . . . . . . . . . * * . . . . . . . I7 . . * . . . . . . . . * * . . . . . . . I8 . . * . . . . . . . * . . * . . . . . . I9 . . * . . . . . . * . . . . * . . . . . I10 . . * . . . . . * . . . . . . * . . . . I11 . . * . . . . * . . . . . . . . * . . . I12 . . * . . . * . . . . . . . . . . * . . I13 . . * . . * . . . . . . . . . . . . * . D2 = = * = * = = = = = = = = = = = = = = P P2 = = P = = = = = = = = = = = = = = = = =
such as was used in the original paper explaining the parity check scheme, known as adaptive cross-parity checking, AXP.
For now, I shall focus, on this page, on classical magnetic tape designs, where all the tracks of the tape were used in one pass (unlike cartridge tape designs that used serpentine recording) and I will not attempt to discuss tapes such as 8mm tape, using the DAT (digital audio tape) format that work like helical-scan videotapes.
Even so, the classic 7-track or 9-track 1/2 inch tape format on 2400-foot reels is, of course, now obsolete. The IBM 3480 tape drive used cartridges containing a reel of 18-track tape. The 3490 included hardware data compression, and the 3490E increased the number of tracks to 36, but only recorded on 18 tracks at a time; the other 18 tracks were used when the tape moved in the other direction. It also increased the recording density, approximately doubling it. The specifications of the 3480 format were described in ECMA-120, those of the 3490 format in ECMA-152, and those of the 3490E format in ECMA-196. Both of these formats have now also been superseded by formats such as that described in ECMA-319, used in IBM's Ultrium-1 member of the Linear Tape Open family of tapes, too modern, advanced, and complicated for me to try to describe here just yet.
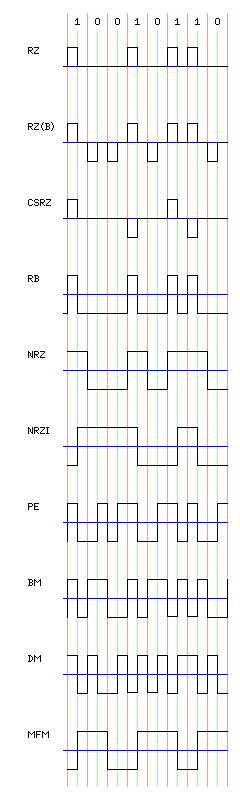
The diagram at the right illustrates the classic methods used to record data on magnetic tapes. Note that for some of the recording formats shown, the area assigned to each bit may be shifted over by half a bit in some other diagrams; the format shown here is that which I felt would be simplest to understand for each recording type.
First, we see Return to Zero (RZ) recording, where a one is represented by a pulse of magnetization in one direction, and a zero is represented by no magnetization.
Then, we see Bipolar Return to Zero (RZ(B)) recording, in which one bits are recorded as pulses of magnetization in one direction, and zero bits as pulses of magnetization in the other direction.
And then we see Carrier-Suppressed Return to Zero (CSRZ) modulation, where pulses represent ones, and the absence of a pulse represents a zero, but successive pulses alternate in direction, thereby avoiding the presence of a DC component in the signal. More bandwidth-efficient forms of modulation which avoid a DC component that we will see later have been used for magnetic recording, but this form of modulation has found applications in fiber-optic communications.
Next, we see Return to Bias (RB) recording. Here, pulses are recorded in one direction for a one bit, but no pulse is recorded for zero.
Then, we see Non-Return to Zero (NRZ) recording. Here, a signal is recorded one way for one, and the opposite way for zero, without space between bits.
Below that, we see Non-Return to Zero Inverting (NRZI) recording, in which a transition from one direction of magnetization to the other indicates a one, and no change indicates a zero. This was a popular method of recording on classic magnetic tapes, and this principle also forms a step within more advanced methods we will see later. (This modulation method is also referred to as NRZ-M, to distinguish it from a complement, NRZ-S, in which a zero bit is indicated by a change in polarity, and a one bit is indicated by the absence of such a change.)
Next, there is Phase Encoding (PE), also known as Biphase Level or Manchester II + 180°. This method was first used when the density of reel-to-reel computer tapes was increased to 1600 bpi. Tapes for use with this method were also labelled 3200 fci, since with this method (like RZ and RB, but unlike NRZ and NRZI) the tape had to be capable of twice as much bandwidth, in the forms of changes of the direction of magnetization, as the raw data itself called for. As is the case with some of the other modulation methods noted here, it was also known by some other names. For example, LINCtape and DECtape used this modulation method, as illustrated by waveform charts in their maintenance manuals, but the customer-level documentation referred to the modulation method used simply as Manchester code, which name properly applies to the next variant of phase encoding to be shown.
Then, we see Biphase Mark (BM), also known as Manchester code and as Frequency Modulation. This variant of phase encoding has a transition at every boundary between bit times, but indicates a one by a polarity transition within the bit, and a zero by no transition within the bit. (Using a transition within the bit to indicate a zero is also possible; this is known as Biphase Space, or Manchester I + 180°.)
After that, we see Differential Manchester (DM) encoding; this version of phase encoding has a polarity transition within each bit, and alternates the direction of this transition when the bits stay the same, and keeps the direction of the transitions constant when the bits differ. Note that this format, unlike the preceding ones shown here, is ambiguous, except for a convention regarding initial conditions, about which bits are ones and which bits are zeroes.
Finally, we see Modified Frequency Modulation (MFM), also known as Miller Code. This combines the low bandwidth requirement of NRZI with the self-clocking characteristic of PE. One can think of it as a modification of NRZI recording, in which a flux change is inserted between two consecutive zero bits. Note that although flux changes can occur either in the middle of a bit, or on the boundary between bits, they still cannot be closer together than the width of a bit. Essentially, room is made for clocking information, without increasing the bandwidth from NRZI, by allowing flux changes at odd half-bit positions. This method is used with floppy disks, and was used with early computer hard drives as well. This method can also be ambiguous, since both a string of consecutive ones and a string of consecutive zeroes lead to a square wave of the same frequency, differing only in phase; the most common way to deal with such an ambiguity is simply to begin a block with a known, fixed sequence of synchronization characters.
When more advanced tapes became available which were capable of 6400 fci, instead of merely using them as 3200 bpi tapes with phase encoding, a way was found to reduce the amount of overhead for self-clocking. This was known as Group Code Recording.
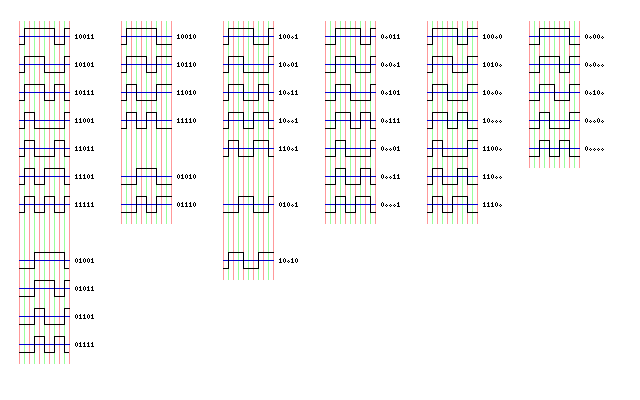
This permitted a tape density of 6250 bpi.
Combinations of five bits, which did not have more than two zeroes in a row, and with not more than one zero at the beginning or end, were recorded using the NRZI technique, but each such combination actually stood for four bits of data.
Seventeen such combinations were available, so the combination 11111, which led to five polarity transitions in a row, could be reserved for synchronization purposes.
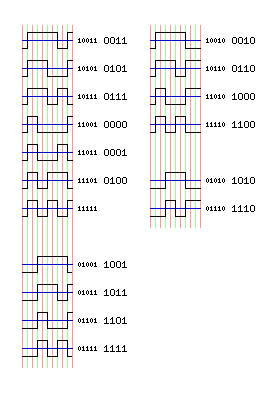
The image above shows how GCR is arranged for decoding purposes, grouping the different symbols by their arrangement of flux changes. The encoding table for GCR is:
0000 11001 1000 11010 0001 11011 1001 01001 0010 10010 1010 01010 0011 10011 1011 01011 0100 11101 1100 11110 0101 10101 1101 01101 0110 10110 1110 01110 0111 10111 1111 01111 sync 11111
with the five coded bits recorded using NRZI, as noted.
The later IBM 3480 cartridge tape used a similar code, but instead of translating four bits to five, it translated eight bits to nine. While the cartridge tape had eighteen tracks, four of those tracks, not two, were used for parity; bytes of data were recorded along the tracks. Two of the parity bits each provided parity for eight of the remaining tracks. The other two parity bits provided a diagonal parity check for the fourteen data bits, one for diagonals in one direction, the other for diagonals in the other direction, as we have seen above.
Allowing five bits to stand for four is certainly more efficient than having two bits stand for one, as in phase encoding. But the MFM method of recording allows just one bit to stand for one, so it is even more efficient. MFM is quite a simple code, and polarity transitions are quite frequent in it. Could a higher density of data be obtained by combining the ability to put transitions at odd positions with the structure of GCR?

If we take the combinations available in IBM's GCR for the 6250 bpi tape drive, and add to them the combinations that would meet the same restrictions on polarity transitions, but with transitions at half-way positions, we increase the number of combinations from 17 to 43.
As 43 is just larger than 32, that lets us represent five bits in the space available for five bits, which is the same density as with MFM. But a possibility for doing better exists.
Of the 43 symbols, 19 of them end either in 0 or in o, which is the notation I am using for an MFM zero as opposed to an NRZI zero, that is, a zero preceded by a phase transition. And, of the 43 symbols, 19 also begin with a zero.
When a symbol that begins with a zero follows a symbol ending in either 0 or o, an extra polarity transition can be inserted between them. Therefore, with two symbols, instead of having 43 * 43 combinations, or 1,849 combinations, which is just over 1,024, and thus which can only encode 10 bits, we now have 43 * 43 plus 19 * 19, or 2,210 combinations. This is now more than 2,048.
But there is no need to get that complicated.
The simplest way to express codes of this type is in the form of binary digits that will later be recorded using NRZI; thus, 1 represents a polarity change, 0 representing no change.
We are looking for a code where there is always at least one 0 between any two ones, then, to represent the fact that a polarity transition can occur at odd positions in terms of the minimum width of a recorded mark on the tape, and where there is also an upper limit to the number of consecutive zeroes.
Let us suppose we would like to achieve a density of four bits in an area of tape that would hold only three bits in NRZI or MFM recording. We could work out a scheme that did so subject to such restrictions by beginning with substitutes for short sequences of bits, and then getting more complicated only to the extent that is necessary to achieve the goal.
If we begin by having every code end in a 1, and begin with a 0, as well as being constrained to have no consecutive ones, and at most seven consecutive zeroes, because, as it happens, a run-length-limited code of the desired density is known to exist, however, our code will start out like this:
00 001 0100 000001 0101 000101 0110 010001 0111 010101 100000 000000101 100001 000010001 100010 000010101 100011 000100001 100100 000100101 100101 010000001 100110 010000101 100111 010010001 101000 010010101 101001 010100001 101010 010100101 10101100 000000010001 10101101 000000010101 10101110 000000100001 10101111 000000100101 10110000 000010000001 10110001 000010000101 10110010 000010010001 10110011 000010010101 10110100 000010100001 10110101 000010100101 10110110 000100000001 10110111 000100000101 10111000 000100010001 10111001 000100010101 10111010 000100100001 10111011 000100100101 1011110000 000000010000001 1011110001 000000010000101 1011110010 000000010010001 1011110011 000000010010101 1011110100 000000010100001 1011110101 000000010100101 1011110110 000000100000001 1011110111 000000100000101 1011111000 000000100010001 1011111001 000000100010101 1011111010 000000100100001 1011111011 000000100100101 1011111100 000010000000101 1011111101 000010000010001 1011111110 000010000010101 1011111111 000010000100001 1100000000 000010000100101 1100000001 000010010000001 1100000010 000010010000101 1100000011 000010010010001 1100000100 000010010010101
and it will not be clear if we are getting anywhere. The reason for this is that if we could compose a short and simple code in which every combination ended in a 1, that code would contain a large amount of self-clocking information. Only a code that had many long and complex combinations would dilute the self-clocking information produced by ending every combination with a 1 enough to leave room for the data.
Thus, we have to choose a different method, one more clever and subtle, of enforcing the constraint that there must be at least one, but no more than seven, zeroes between each pair of ones.
Let us only allow up to five zeroes at the beginning of our codes, requiring one zero, and let us allow only up to two zeroes at the end.
Then, the code starts out like this:
00 001 01 010 1000 000001 1001 000010 1010 000100 1011 000101
We seem to have run out of codes.
But if we code the sequence 01, and get 010, it can be legitimately followed by 100; this can't begin any code, however, because some codes end in a 1. So there are some codes we can safely add:
1100 010100 1101 010101 111000 000010100 111001 000010101 111010 000100100 111011 000100101
Since some of these codes end in a zero, we can repeat the process:
111100 010100100 111101 010100101 11111000 000010100100 11111001 000010100101 11111010 000100100100 11111011 000100100101
and repeat it again:
11111100 010100100100 11111101 010100100101 1111111000 000010100100100 1111111001 000010100100101 1111111010 000100100100100 1111111011 000100100100101
It looks like things are getting no worse, and no better. This implies we will be able to express arbitrary bit strings within our length constraint, but we need a better way to express the code we're using, so that we don't have codewords of infinite length.
We need to have a code that is stateful, it seems.
An initial attempt at one seems to run into the same problem of infinite regress:
A B
00 000 B 001 A
01 001 A 010 A
10 010 A 100 A
11 101 A
1100 010100 A
1101 010101 A
111000 000010100 A
111001 000010101 A
111010 000100100 A
111011 000100101 A
But if we change how we look at things a bit, the code can become simple:
A B
00* 001 B 001 B
01 010 A 000 A
10 100 A 010 A
11* 101 B --
*0011 010000 A 010000 A
*1111 100000 A
Oh, wait, we can do better than that...
A B
00* 001 B 001 B
01 010 A 010 A
10 100 A 000 A
11* 101 B --
*0011 010000 A 010000 A
*1111 100000 A
No equivalent for 11 is given in state B, because the codes (in either state) that lead to state B are footnoted; instead of their normal three-bit outputs being followed by any three-bit code, the three-bit equivalent of the two-bit input is replaced by a three-bit value that can be followed by one of five possible values, only four of which are actually possible in state A.
This code is very similar one well-known RLL(1,7) code, the one discussed in a 1984 paper by Jacoby and Kost. The fact that there are only two states involved, however, is more closely reminiscent of U.S. Patent 4,413,251, to Adler, Hassner, and Moussouris of IBM.
Since two polarity transitions are always separated by one period without a transition, the encoded bits are output at twice the baud rate of the outgoing signal, but three encoded bits represent two data bits. Thus, one data bit equals one and one-half encoded bits, and three-quarters of a baud. For comparision, the elaborate and complicated GCR-based scheme I devised above is an RLL(1,6) code which encodes 11 bits in 10 bauds, and MFM can be viewed as an RLL(1,3) code which encodes one bit per baud; this is still a considerable improvement over phase encoding, which encodes one bit in two bauds, since, as noted, like PE, but unlike NRZI, MFM is also self-clocking. In fact, the GCR code itself can be viewed as an RLL(0,2) code as well.
Currently, most hard drives do use an RLL(1,7) code. If the minimum span between flux changes was divided into three parts, and an RLL(2,7) code were used, as was used on the first hard disk drives to increase density beyond what MFM provided, we don't need to get so complicated.
In that case, we can have a coding scheme such as:
00 0001 01 0010 100 000001 101 000010 110 001001 1110 00000010 1111 00001001
Since this RLL(2,7) code encodes two data bits as four encoded bits, but three encoded bits make a baud, each data bit requires two-thirds of a baud in this scheme.
A code of this type was described in U. S. Patent 3,689,899, to P. A. Franaszek, also of IBM, which described a scheme of RLL(1,8) encoding with the same data density as the later RLL(1,7) codes; he later improved that to RLL(1,7) which preceded slightly the one devised by Cohn, Jacoby, and Bates, and described in the paper by Jacoby and Kost.
This code was itself preceded by an RLL(2,11) code which had the same data rate, which was known as 3PM, also devised by Jacoby.
Other desirable properties that a coding for magnetic tape may require include limiting or eliminating the DC component of the code; that is, having an equal number of zeroes and ones on the tape (that is, after NRZI encoding has been applied). Two ways of recording data on tape which had this desirable property were ZM (Zero Modulation), invented by Arvind Patel at IBM, and used in the IBM 3850 data storage system, and the code known as Miller Squared, used in the Ampex D2 digital videotape recording format. Both of these coding methods use Modified Frequency Modulation, also known as Miller Code, as their starting point, and operate by modifying some transitions.
The following diagram illustrates how the Miller II code works:
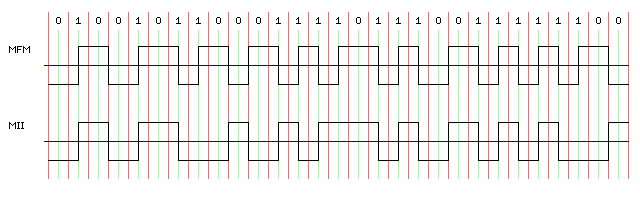
The transition in the middle of the bit time, for the last bit in a sequence of an even number of one bits, is omitted. The bit can be distinguished from a zero by the fact that there is no transition between it and the zero bit that follows; in MFM, two zero bits in succession always have a polarity transition between them.
Zero Modulation, which was designed earlier, is considerably more complicated.
Since RLL(1,7) encoding requires only 3/4 of a baud for a bit, this means each baud contains 1 1/3 data bits. Thus, 6 bauds contain 8 data bits. One could, therefore, imagine a 7-track tape drive set up to record the parity bit using MFM in one track, with the other six tracks containing data in RLL(1,7) code. (Since MFM is an RLL(1,3) code, using it in one track would provide additional timing signals.) Or one could use the central seven tracks of a 9-track tape in this way, putting timing tracks on the two outer tracks, for a tape that provided random access features like those of DECtape:
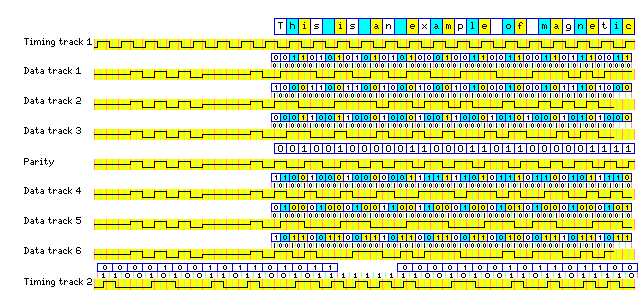
Timing track 1 simply consists of a steady stream of pulses, the transitions of which always occur in the middle of the first half of a bit time. One possible pattern that might be considered for timing track 2 would be a steady stream of pulses which always make transitions in the middle of the second half of a bit time. Another possibility is a short mark and a short space, with transitions in the middle of the second half, followed by a long mark and a long space, with the transition between them in the middle of the first half; this allows occasional measurements of the offset between the two timing tracks, and marks off the tape into somewhat longer divisions of time.
If the tape is intended for random access use, however, it would be useful to be able to determine one's absolute position across the entire length of the tape. The opportunity to throw in GCR for good measure, so that all transitions would occur in the middle of the second half of the bit time, in addition to MFM and RLL(1,7), was also too much for me to pass up. The 16 bit binary numbers are recorded one after another, each separated by the unallocated 11111 synchronization symbol, so each 16 bit number takes up 25 baud on the tape.
One immediate question, however, about this format would be that, since parity is meant to deal with errors likely to occur on the tape in actual practice, irrespective of the meaning of the data recorded on the tape, it seems that the parity track should be in MFM and not RLL(1,7), so as to detect errors in each column on the tape. However, since the data will be used in eight-bit form, it does make sense to know which eight-bit characters are to be rejected.
Note that the diagram uses the "old" version of the RLL(1,7) code. Also note that it can be readily seen from the diagram that MFM produces a higher number of polarity transitions than RLL(1,7), with GCR producing a number of transitions intermediate between those other two codes. Since the timing tracks and the parity track provide a considerable amount of clocking information, the data tracks could make use of 3PM, an RLL(1,11) code with even longer possible times between transitions, instead of an RLL(1,7) code if desired.
Also note that the lead-in from the gap between blocks is shown as having the same polarity for all seven inner tracks. This will be true if the block was recorded while the tape was moving forwards, but then a similar lead-out in reverse at the end may have different polarities in different tracks. If the block had been recorded in reverse, all seven lead-out sequences would have the same polarity, and the lead-in sequences would have random polarities. (I also have not dealt with any complexities that may arise as a result of trying to record data in RLL(1,7) while writing backwards. Perhaps all that would be needed is a polarity transition at the beginning of the block to indicate starting in state B, or the first/second half of a six-bit backwards code...)
For the example, no overhead data is shown, only text; in practice, while it would only be necessary to have the CRC at one end of the block, unlike DECtape, presumably data such as text would be preceded by things such as a file header, a two byte record length field preceding each record, directory entries, and so on, since this is a tape format intended for random access.
There are other ways to combine the various principles we have seen. Here, a denser form of recording was used for data than for parity, because parity was applied to eight-bit characters on six data tracks. If one has a full eight data tracks, one might do the reverse; record data using GCR, but use MFM for the parity, so that the parity applies to the bits actually on the tape, after GCR encoding, for example. Longitudinal parity could be applied to the data prior to GCR encoding on the basis of a four-way interleave, thereby avoiding interactions between encoding and parity; and, if being able to tolerate a high error rate more than doubles the possible recording density, then encoding 48 bits of data on each track at a time, using the Golay code, might even make sense.
As for the timing tracks, an obvious and simple way to get by with only one timing track would be to use phase encoding for the timing track. This would lead to a regular succession of transitions; the fact that the block numbers, also encoded on the track, would be recorded at only half the bandwidth would hardly be an issue.
For the sake of completeness, some important facts about analog magnetic tape recording are noted here as well.
One important property of the materials used in magnetic tapes that helps protect them from being damaged by stray magnetic fields is that those materials do not respond linearly to an applied magnetic field. Small magnetic fields will have very little effect on them, compared to the effect that a stronger field would have.
This would cause severe third-harmonic distortion if an audio signal were directly applied to the record head of a magnetic tape recorder.
An early method used to surmount this was to apply a DC bias to the audio signal. This placed the signal in the nearly linear region of the magnetic material's response. However, that region might not be perfectly linear, and so for louder sounds, its gradual change to a smaller response to an applied signal might be noticeable as second-harmonic distortion.
The method currently used on audio tape recorders is AC bias. The audio signal is added to a signal of a much higher frequency before being applied to the tape. In this way, if, even in the linear region of the material's response, there is still a gradual decline in response at lower levels, it will tend to cancel out.
For even better results, analog data recorders used in instrumentation use FM recording, since the distortion involved in magnetic tape recording does not affect the location of the zero crossings of the applied signal. Video tape recorders combine FM recording, for the black-and-white portion of the video signal, with the use of the FM signal as an AC bias for the color portion of the video signal. Modern videocassette recorders also arrange for the phase of the color signal to be such as to cause crosstalk from the two tracks adjacent to a given diagonal stripe across the tape to largely cancel out.