[Next] [Up]
[Previous] [Index]
Quadibloc 2002C
Quadibloc 2002C is a block cipher with a block size of 80 bits. This
unusual block size makes it simple to devise a cipher illustrating the
particular type of unbalanced Feistel round which serves as the underlying
principle of this cipher.
There are two types of round in Quadibloc 2002C. The first type of round,
which shall be referred to as the Type A round,
uses an f-function of 16 bits of the block to control two Feistel rounds
using the standard Quadibloc f-function which modify the other 64 bits of
the block, and is as illustrated below:
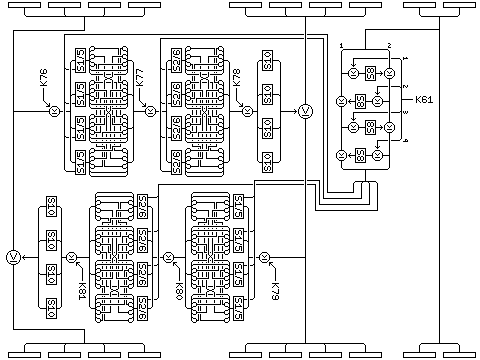
The second type of round uses two Feistel rounds with the standard
Quadibloc f-function as an f-function in itself, by means of which 64 bits
of the block produce a 64 bit value used to modify the other 16 bits of
the block. This round, the type B round, is illustrated here:
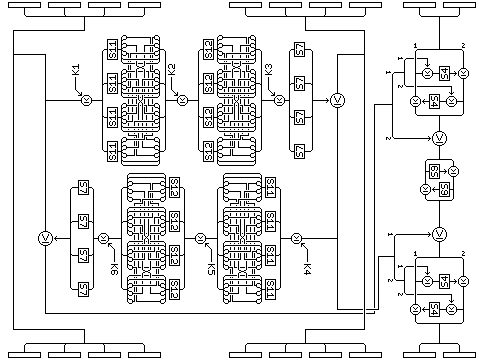
The type B round is felt to contribute to the strength of the cipher
because it shares with some of the better stream ciphers the characteristic
that the modification of the block which it produces, while it contains
only 16 bits of information, depends on 64 bits of input, and on 192 bits
of subkey, thus making it difficult to work backwards to make deductions
concerning the subkeys. However, the fact that the effects of the subkeys
are confined to 16 bits of the block means that this round produces slow
diffusion by itself, and thus it is complemented by the type A round.
The Cipher in Detail
The encipherment of an 80-bit block of plaintext by means of Quadibloc
2002C shall consist of the following steps:
- Five type A rounds, each one followed by a plain byte permutation.
- Five sequences of one type A round, followed by one type B round,
followed by a twisted byte permutation.
- Five type A rounds, with a plain byte permutation between each pair
of them, for a total of four byte permutations.
- Five sequences of a twisted byte permutation, followed by a type B
round, followed by a type A round.
- Five type A rounds, each one preceded by a plain byte permutation.
A plain byte permutation takes the ten bytes in a block from the
order:
1 2 3 4 5 6 7 8 9 10
to the order:
3 4 9 1 8 10 5 6 2 7
and a twisted byte permutation takes the ten bytes in a block from
the order:
1 2 3 4 5 6 7 8 9 10
to the order:
10 1 2 3 9 5 6 7 4 8
thus, the plain byte permutations are used between type A rounds so as to
preserve alternation between the left and right halves of the Feistel round,
while the twisted byte permutation is used when type B rounds are also
present, since in that case, the two additional bytes are modified together,
and thus they can be swapped between streams. Also note that the plain byte
permutation rotates the two groups of five bytes by either two or three
bytes per step, while the twisted byte permutation rotates a loop including
all ten bytes by only one byte per step. Thus, the plain byte permutation
brings different bytes of each half of the block into corresponding
positions in succeeding rounds.
The type A round proceeds as follows:
The block is divided into ten bytes, numbered 0 through 9 from left
to right.
- A copy of bytes 8 and 9 are enciphered by means of four miniature
Feistel rounds as follows:
- A copy of byte 8 is XORed with the leftmost byte of the current
subkey for this purpose (K61 for the first type A round, K62 for the
next, and so on), the element of the key-dependent S-box S8 to which
it is the index is taken, and that result is XORed with the copy of
byte 9, modifying it.
- A copy of byte 9 is then XORed with the second leftmost byte
of K61 or the successor thereof, it is used as an index into S8,
and the result is XORed with the copy of byte 8, modifying it.
- Using the third and fourth bytes of K61 or its successor,
two additional Feistel rounds following the pattern of those preceding
are performed.
- The 16-bit result of these Feistel rounds is used, a bit at a time,
to select S boxes for standard Quadibloc f-functions.
- A copy of bytes 0 to 3 is used as input into a standard Quadibloc
f-function, the output of which is XORed with bytes 4 to 7, modifying
them. The f-function proceeds as follows:
- Subkey K76 is XORed with the copy of bytes 0 to 3 in the first
Type A round, subkey K82 used in the next, increasing by six with
each round.
- The first four bits of the 16-bit result above select between
S-boxes 1 and 5 as derived from Euler's Constant in the first
subsitution/permutation layer of the f-function. The permutation
layer is as described previously for other ciphers of the Quadibloc
series.
- Subkey K77 or the successor thereof is XORed with the
result.
- The next four bits
of that result select between S-boxes 2 and 6 in the second
substitution/permutation layer.
- Subkey K78 or the successor thereof is XORed with the result.
- The bytes of the result are replaced by their substitutes
from key-dependent S-box S10.
- A copy of bytes 4 through 7 as modified is then used as
input to a similar f-function, using the latter eight bits
of the result of the small Feistel rounds applied to a copy
of bytes 8 and 9, and subkeys K79, K80, and K81 in the first
type A round or the successors thereof, and the result is
XORed with bytes 0 through 3, modifying them.
The type B round proceeds as follows:
- A copy of bytes 0 through 7 is used as input to two
Feistel rounds using the Quadibloc f-function. In the
first round, bytes 0 through 3 are the input, bytes 4
through 7 are modified, the subkeys are K1, K2, and K3
in the first type B round, incremented by 6 between rounds,
and the S-boxes are S11 and S12 as derived from Euler's
constant in the two S/P layers, and the key-dependent
S-box S7 at the end. In the second Feistel round within the
first Type B round, subkeys K4, K5, and K6 are used,
and the modified bytes 4 through 7 are used as input to
produce a result modifying the copy of bytes 0 to 3.
- The 64-bit result is used to modify bytes 8 and 9,
the only bytes of the block actually changed by a Type B
round, as follows:
- A copy of byte 8 is XORed with the first byte of
the eight-byte result, used as an index into S-box S4
as derived from Euler's constant, and the result is
XORed with byte 9.
- A copy of byte 9 is XORed with the second byte of
the eight-byte result, used as an index into S-box S4,
and the result is XORed with byte 8.
- The third and fourth bytes are XORed with bytes
8 and 9 in a 16-bit XOR operation.
- A copy of byte 8 is used as an index into key-dependent
S-box S9, and the result is XORed with byte 9.
- A copy of byte 9 is used as an index into key-dependent
S-box S9, and the result is XORed with byte 8.
- The fifth and sixth bytes are XORed with bytes
8 and 9 in a 16-bit XOR operation.
- A copy of byte 8 is XORed with the seventh byte of
the eight-byte result, used as an index into S-box S4,
and the result is XORed with byte 9.
- A copy of byte 9 is XORed with the eighth byte of
the eight-byte result, used as an index into S-box S4,
and the result is XORed with byte 8.
The Key Schedule
The subkey material used by Quadibloc 2002C is as follows:
- Sixty 32-bit subkeys, K1 through K60, used in the ten type B rounds,
six to a round, for the two Feistel rounds which serve as the f-function
by which 64 bits of the block modify the other 16 bits;
- Fifteen 32-bit subkeys, K61 through K75, used in the small Feistel
rounds within the type A rounds, which serve as the f-function by which
16 bits of the block control the large Feistel rounds through which the
other 64 bits of the block are modified;
- Ninety 32-bit subkeys, K76 through K165, used in the main Feistel rounds
of the type A rounds, six to a round;
- Four bijective S-boxes containing a permutation of the values from 0
to 255, S7, S8, S9, and S10.
Subkey generation proceeds in the following order:
- K1 through K60 are generated.
- S7 is generated.
- A noninvertibility operation is performed.
- K61 through K75 are generated.
- S8 is generated.
- A noninvertibility operation is performed.
- S9 is generated.
- A noninvertibility operation is performed.
- K76 through K165 are generated.
- S10 is generated.
The purpose of the noninvertibility operation is to serve as a one-way
function, like a hash function, so that even if information about K76
through K165, the subkeys used in the most conventional manner in
Feistel rounds whose result is directly manifest in the relation between
plaintext and ciphertext, can be obtained through methods such as
differential cryptanalysis, this information will not lead to information
about subkeys K1 through K60, which are in the portion of
the cipher which is hidden away from analysis because it affects only
16 bits of the block at a time.
The key will be a multiple of four bytes in length, and must be at least
eight bytes in length.
Once again, the methods used to generate subkey bytes and key-dependent
permutations are as follows:
Initialization
Three strings of bytes of different length are produced from
the key.
The first string consists of the key, followed by one byte containing the
one's complement of the XOR of all the bytes of the key.
The second string consists of the one's complements of the bytes of the
key in reverse order, with three bytes appended containing the following three
quantities:
- The sum, modulo 255, of the bytes of the key, incremented by one by normal
addition. (Thus, this produces a number from 1 to 255.)
- The XOR of all the bytes at odd numbered positions in the key, where the
first byte in the key is considered to be byte 1, and odd.
- The one's complement of the XOR of all the bytes at even numbered positions
in the key.
The third string consists of alternating bytes, taken from the bytes of the
key in reverse order, and then from the bytes of the one's complement of the
key, and then that string is followed by the one's complements of the
first four bytes of the key.
Thus, if the key is:
128 64 32 16 8 4 2 1 1 2 3 4 5 6 7 8
then the strings generated from it are as follows:
First string:
128 64 32 16 8 4 2 1
1 2 3 4 5 6 7 8
8
Second string:
247 248 249 250 251 252 253 254
254 253 251 247 239 223 191 127
37 170 93
Third string:
8 127 7 191 6 223 5 239
4 247 3 251 2 253 1 254
1 254 2 253 4 252 8 251
16 250 32 249 64 248 128 247
127 191 223 239
Given that the length of the key is 4n, the lengths of the three strings
are 4n+1, 4n+3, and 8n+4, and hence all three are relatively prime, since
both 4n+1 and 4n+3 are odd, and 8n+4 is two times 4n+2.
Two buffers, each containing room for 256 bytes,
are filled by generating bytes from the first and second
strings by placing them in a nonlinear shift register.
The form of that shift register is shown in the following illustration,
showing its precise form for the first string.
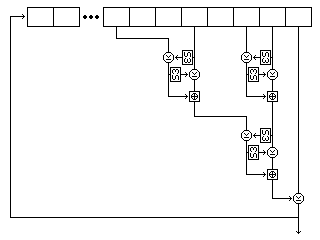
Five bytes are read from the string at each step. For the first string,
they are, as shown in the diagram, the eighth-last, fifth-last, third-last,
and second-last
bytes and the last byte.
For the second string, they are the eighth-last,
seventh-last, fourth-last, and second-last bytes, and the last byte.
For the third string, they are the twelfth-last, tenth-last,
seventh-last, and fourth-last bytes, and the last byte.
Each time the shift register produces a byte, it does so as follows:
- The second byte read is used to select an entry in S-box S3, and the
value of this entry is XORed to the first byte. Then the first byte
is used to select an entry in S-box S3, and the value of this entry is
XORed to the second byte.
- The fourth byte read is used to select an entry in S-box S3, and the
value of this entry is XORed to the third byte. Then the third byte
is used to select an entry in S-box S3, and the value of this entry is
XORed to the fourth byte.
- The first and second bytes, as modified, are added together
using modulo-256 addition to form a first result.
- The third and fourth bytes, as modified, are added together
using modulo 256 addition to form a second result.
- The second result is used to select an entry in S-box S3, and the
value of this entry is XORed to the first result. Then the first result
is used to select an entry in S-box S3, and the value of this entry is
XORed to the second result.
- The two results as modified are added together using modulo 256
addition to form a third result.
- The fifth byte read, which is always the last byte in the shift
register, is XORed with the third result. The resulting value is
output as the byte produced by operating the shift register.
- The values in the shift register are modified by removing the last
byte, advancing the bytes in the shift register to the next later
position, and appending the output result as the new first byte of
the shift register contents.
Both buffers contain 256 bytes. The first buffer, called buffer A, is filled
with 256 successive bytes generated from the second string by means of
a nonlinear shift register filled with the second string.
The second buffer, called buffer B, is filled with 256 successive bytes
generated from the first string by means of the nonlinear shift
register filled with the first string.
Subkey Byte Generation
Once the setup is complete, subkey material is generated one byte at
a time, the first byte generated being the leftmost byte of subkey K1, and
so on.
A subkey byte is generated as follows:
- A byte is generated from the first string by the nonlinear shift register
operation.
- The byte at the position in buffer A indicated by this value is taken, and
is called P.
- A byte is generated from the third string by the nonlinear shift register
operation. In the case of the third string, the shift register operation
involves the following five bytes: the twelfth, tenth, seventh, and fourth last
bytes, and t
byte. The value of the byte thus produced is placed in buffer A, replacing the
- A byte is generated from the second string by the nonlinear shift register
operation.
- The byte at the position in buffer B indicated by this value is taken, and
Q.
- A byte is generated from the third string by the nonlinear shift register
operation. Its value is placed in buffer B, replacing the value taken.
- The subkey byte generated is the XOR of P and Q and an additional byte
generated from the third string by the nonlinear shift register operation. (The
use of an additional byte from the third string ensures that all the bytes of
the key participate directly in the key schedule; otherwise, some could be
skipped over in a sense as a result of
the selection of bytes to use from the buffers.)
The following diagram attempts to illustrate the complete process of
subkey byte generation:
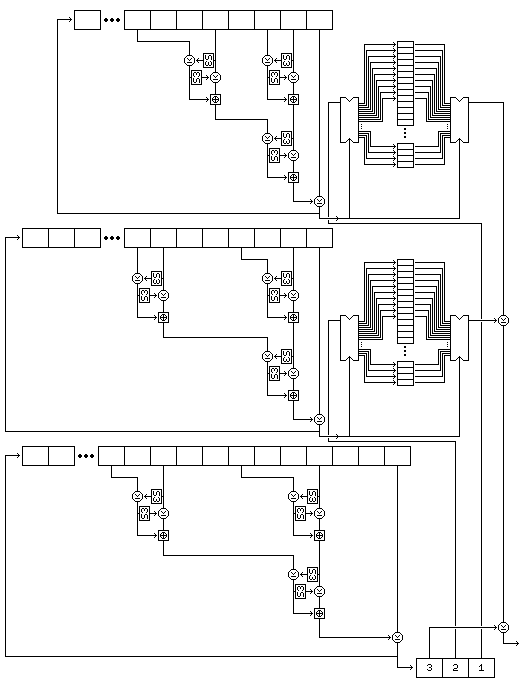
Note that this procedure, since it exercises the two strings used to select
bytes, rather than the string used to generate values, results in a small
change in the key bringing about large changes in the subkeys from the very
beginning, although it is still true, since the bytes used to select buffer
contents could be the same by coincidence, that subkeys generated from very
similar keys have a slightly enhanced probability of having bytes in
common.
Permutation Generation
During subkey generation, the key-dependent
S-boxes S7, S8, S9 and S10 must be generated.
To generate each bijective S-box, the following procedure is used:
- 256 bytes are generated following the same procedure as for subkey byte
generation, and these bytes are placed in a 256-byte buffer called buffer C.
- A 256-byte buffer called buffer D is filled with the numbers from 0 to 255
in order.
- For every i from 0 to 255, if element i of buffer C (hereinafter called
C(i)) is not equal to i, swap elements i and C(i) of buffer D.
- For every i from 0 to 255, if B(i) is not equal to i, swap elements
i and B(i) of buffer D.
- For every i from 0 to 255, if A(i) is not equal to i, swap elements
i and A(i) of buffer D.
The resulting contents of buffer D are used as the key-dependent
bijective S-box intended to be produced. Note that this is a
procedure, introduced for Quadibloc X, is more straightforwards than
the other two basic procedures used previously to produce S8 in other
ciphers in this series.
This procedure, although it uses buffers A and B, leaves them undisturbed;
thus, byte generation may continue after one S-box is produced.
The Noninvertibility Operation
The noninvertibility operation, a step in this plan of subkey generation
introduced especially for Quadibloc 2002C, consists of generating as many
bytes of subkey material as there are bytes in the three shift registers used
the initial contents of which were derived from the keys, as well as an
additional 512 bytes of subkey material, and then XORing this subkey material,
in order, with the bytes of those three shift registers, the bytes of buffer A,
and the bytes of buffer B.
Long Keys
The subkey generation procedure given above works well for keys from 64 bits
to 1,024 bits in length. When the length of the key approaches 2,048 bits in
length, however, the first two shift registers are no longer thoroughly mixed
by filling buffers initially.
Thus, the following modified subkey generation procedure is given for keys
which are more than 1,024 bits long. A key must still be a multiple of 32 bits
in length:
- (1) Divide the key into blocks of 512 bits until the remaining part of the
key is from 512 to 992 bits in length.
- (2) Use the first block of the key as the key for the normal Quadibloc
2002C key schedule.
- (3) Continue to generate enough additional subkey bytes to XOR these with
the block into which the key was divided.
- (4) Use the next block, after the XOR, to carry out the Quadibloc 2002C
key schedule, except:
- The subkey material generated is XORed with the previously generated values
of the subkeys;
- (This is different for Quadibloc 2002C) For the second, and
all subsequent even-numbered, blocks, generate the values used to modify the
existing keys in the reverse sequence
of groups between noninvertibility operations, but in the normal order within
each one (for odd-numbered blocks, use the initial order); that is:
- K76 through K165 are generated.
- S10 is generated.
- A noninvertibility operation is performed.
- S9 is generated.
- A noninvertibility operation is performed.
- K61 through K75 are generated.
- S8 is generated.
- A noninvertibility operation is performed.
- K1 through K60 are generated.
- S7 is generated.
- Generate permutations for key-dependent S-boxes S7 through S10 in the
normal sequence of generation, and then modify the S8 and S9 to be used in the
cipher as follows: go through the newly-generated S-box and the previously
calculated corresponding S-box from positions 0 to 255; in a new
array, place the value in the new permutation in the position indicated by the
value in the original permutation. Once this is finished, the new array is the
replacement permutation.
- (5) If there are any additional blocks remaining in the key, go back to ste
This method ensures that the key schedule is a function of the entire
key. It also is expected to ensure that there is no usable relationship between
the groups of keys separated by noninvertibility operations.
[Next] [Up]
[Previous] [Index]
Next
Start of Section
Skip to Next Section
Skip to Next Chapter
Table of Contents
Main Page




