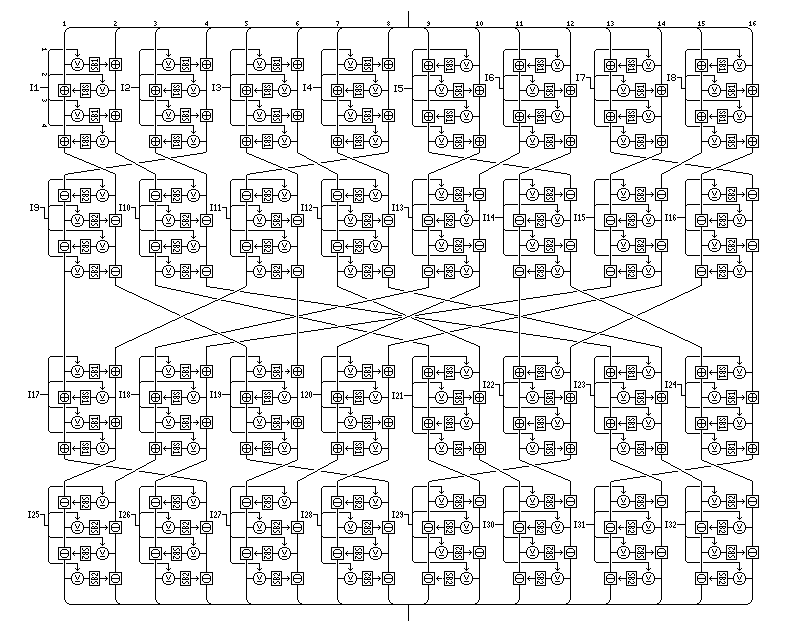
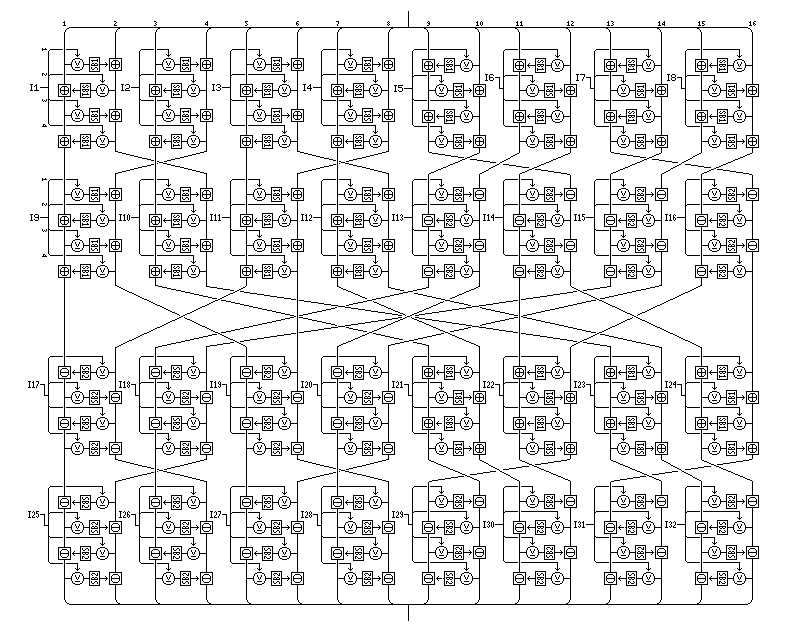
The standard rounds of this cipher, which do perform genuine encryption, and thus cannot be described as merely being a mixing and whitening phase, are a modified form of the Quadibloc 2002A round.
An enlarged form of the diffusion phase, where the pseudo-Hadamard transform with a key-dependent S-box added is replaced by a keyed mini-Feistel cipher with four rounds, as illustrated below:

is an element of this cipher. Note that the in-place Feistel rounds have their left and right halves reversed in the right half of the block. Note also that the byte interchange between the layers has been changed.
The byte interchange between the first and second layers has been changed to move the bytes as shown below:
from: 1 2 3 4 to: 4 1 2 3
in the left half, and
from: 1 2 3 4 to: 2 3 4 1
in the right half.
This is reversed between the third and fourth layers, so that the arrangement can be its own inverse if the subkeys are suitably shifted, and if the key-dependent bijective S-boxes SB1 and SB2 are switched. (Because of the number of different elements in the cipher, the key-dependent S-boxes, instead of being numbered starting with S8, are given their own number series.)
The reason for this change is so that for the eight Feistel rounds that make up the first two layers, and the eight Feistel rounds that make up the last two layers, left and right halves of the Feistel rounds will strictly alternate. No attempt, however, has been made to retain the alternation across the gap between the second and third layers, since the diagonal transpose used there is needed to retain the self-inverse property.
Because of the self-inverse property, this enhanced diffusion phase alternates with a diffusion phase which, although more similar to that used in Quadibloc 2002A, also is changed in terms of the byte interchange and the orientation of the rounds in the same way:
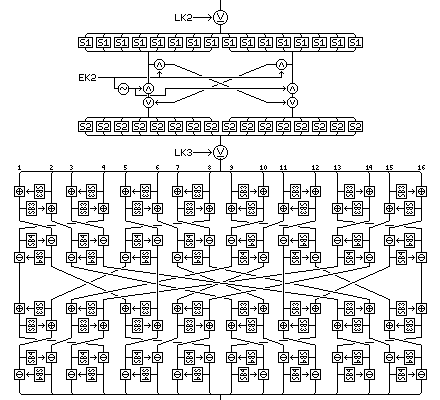
and which becomes its own inverse if the roles of key-dependent S-boxes SB3 and SB4 are interchanged.
In this diagram, the operations that take place between the rounds are also illustrated.
Incidentally, note that the operation interchanges the bytes from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
8 10 14 4 5 11 15 1 16 2 6 12 13 3 7 9
This arrangement is, of course, self-inverse. Since it is a rearrangement, however, what are its implications for the effects of subsequent swap halves operations on diffusion? Unfortunately, they are very poor; the same bytes correspond on opposite halves of the block after this rearrangement as before.
This can be improved by changing how bytes are rearranged after the first set of small Feistel rounds from 4 1 2 3 8 5 6 7 10 11 12 9 14 15 16 13 to 4 1 2 3 6 7 8 5 12 9 10 11 14 15 16 13 and similarly making the rearrangement between the third and fourth layers the inverse of that. This retains the property that left and right sides of Feistel rounds alternate, and it still ensures each byte interacts indirectly with each other byte, but it avoids this excessive symmetry, causing the overall interchange of the four layers to become: 6 12 14 4 15 1 7 9 8 10 16 2 13 3 5 11 which ensures that all corresponding bytes in opposite halves were originally in the same half before, thus maximizing the additional diffusion provided by successive swap halves steps. However, since all the bytes are thoroughly mixed by the operation, this improvement may not seem necessary, since in a sense, the same thing, a function of all the previous bytes, is always being diffused. The diagram below shows how the previous diagram appears after having been modified to reflect this change: |
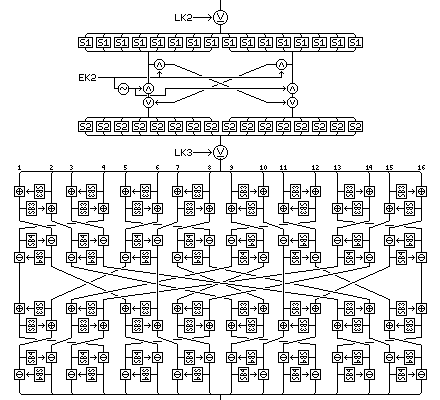
When this modification is made both to the lesser diffusion rounds, as shown above, and to the greater diffusion rounds as well, the resulting cipher becomes Quadibloc 2002EC (corrected). However, it is possible to do even better than this. Since the greater diffusion phases are different from the lesser diffusion phases, if they are modified in a different manner, then it could take four rounds, rather than two rounds, for the bytes to return to their original positions, thus allowing the bit swap operations to provide additional diffusion. One way of doing this is illustrated below: |
Here, the layer structure has been changed for half the block, so that instead of alternating between the use of the two S-boxes, and between addition and subtraction, in layers, the same operation is used for two layers at a time. This makes the kind of byte interchange needed between the layers of the first and second pairs to preserve the alternation between left and right halves of the Feistel rounds completely different. Thus, between the first and second layers, the interchange is from 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 to 1 4 3 2 5 8 7 6 10 11 12 9 14 15 16 13 and between the third and fourth layers, the interchange is from 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 to 1 4 3 2 5 8 7 6 12 9 10 11 16 13 14 15 resulting in the overall interchange of the four layers becoming: 1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9 Here, although corresponding bytes in opposite halves are still from opposite halves, they are not the original partners of the bytes on opposite halves before the interchange, so diffusion is still increased, but in a different way. The net result of this reform of the greater diffusion phase combined with the previous change applied to the lesser diffusion phase is that the bytes interact as follows: They begin as independent bytes: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 After the first bit swap phase, they are mixed as follows: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 10 11 12 13 14 15 16 1 2 3 4 5 6 7 8 where, under the number of each byte, is the number, in the original ordering, of the other byte with which it has swapped bits. After a greater diffusion phase, the ordering of the bytes is changed to this: 1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9 9 6 2 13 12 7 3 16 8 11 15 4 5 10 14 1 Then, the second bit swap phase causes further mixing, so that the bytes now include bits from other bytes as shown here: 1 14 10 5 4 15 11 8 16 3 7 12 13 2 6 9 9 6 2 13 12 7 3 16 8 11 15 4 5 10 14 1 16 3 7 12 13 2 6 9 1 14 10 5 4 15 11 8 8 11 15 4 5 10 14 1 9 6 2 13 12 7 3 16 The different rearrangement of the lesser diffusion phase, when applied to this, changes the ordering of the mixed bytes to: 15 12 2 5 6 1 11 16 8 3 9 14 13 10 4 7 7 4 10 13 14 9 3 8 16 11 1 6 5 2 12 15 2 5 15 12 11 16 6 1 9 14 8 3 4 7 13 10 10 13 7 4 3 8 14 9 1 6 16 11 12 15 5 2 and the following bit swap phase mixes bits which now, potentially, come from the original bytes: 15 12 2 5 6 1 11 16 8 3 9 14 13 10 4 7 7 4 10 13 14 9 3 8 16 11 1 6 5 2 12 15 2 5 15 12 11 16 6 1 9 14 8 3 4 7 13 10 10 13 7 4 3 8 14 9 1 6 16 11 12 15 5 2 8 3 9 14 13 10 4 7 15 12 2 5 6 1 11 16 16 11 1 6 5 2 12 15 7 4 10 13 14 9 3 8 9 14 8 3 4 7 13 10 2 5 15 12 11 16 6 1 1 6 16 11 12 15 5 2 10 13 7 4 3 8 14 9 which does indeed avoid duplication. |
Quadibloc 2002E, where the lesser diffusion phase is modified as in Quadibloc 2002EC, and the greater diffusion phase is modified as shown above, becomes Quadibloc 2002EM (maximum).
The S-box S1 is the same one as used in Quadibloc 2002A:
232 116 188 183 118 218 184 40 137 185 157 230 200 130 31 100 140 178 126 206 237 222 220 147 70 36 53 254 111 210 204 14 78 255 71 76 25 84 64 239 7 180 60 75 169 217 225 82 203 73 141 94 109 26 182 63 181 103 158 145 42 142 97 55 38 159 201 186 80 151 24 34 173 49 129 43 35 252 32 150 68 171 47 248 37 221 238 101 127 153 155 162 134 253 51 120 107 62 131 233 15 87 161 57 174 170 240 96 243 52 196 28 235 216 231 122 1 195 4 128 95 245 115 152 125 124 18 88 119 74 13 98 191 242 92 229 138 8 136 172 16 50 61 241 214 59 198 23 228 164 79 69 123 89 175 90 234 10 58 65 227 102 91 211 149 179 213 246 197 44 105 81 139 72 104 154 207 189 17 165 41 56 54 3 6 9 67 215 2 177 193 132 223 190 199 117 110 168 146 194 12 66 209 48 30 251 19 176 224 202 29 163 244 166 144 187 113 45 5 247 22 85 21 192 208 46 250 160 148 135 11 114 0 99 156 112 249 20 86 39 106 143 133 108 212 121 167 219 83 236 226 205 77 93 27 33
and the second self-inverse S-box, derived from the original S2 defined in the page on Euler's Constant and the Quadibloc S-boxes in the same fashion, is the following:
68 196 12 96 92 226 20 180 242 48 153 237 2 121 125 232 253 154 249 28 6 214 73 109 58 116 100 136 19 255 31 30 219 163 167 57 140 119 53 228 210 89 224 122 62 202 93 151 9 171 191 190 175 38 104 201 95 35 24 208 129 250 44 229 127 148 74 131 0 215 245 88 90 22 66 221 85 184 238 179 110 165 173 139 126 76 115 132 71 41 72 169 4 46 113 56 3 143 235 117 26 243 177 246 54 223 118 195 135 23 80 199 182 94 176 86 25 99 106 37 188 13 43 241 225 14 84 64 145 60 194 67 87 152 193 108 27 144 212 83 36 142 141 97 137 128 239 220 65 218 157 47 133 10 17 156 155 150 211 187 185 172 174 33 240 81 203 34 251 91 209 49 161 82 162 52 114 102 233 79 7 230 112 244 77 160 252 159 120 248 51 50 234 134 130 107 1 198 197 111 213 55 45 166 247 217 231 254 59 170 40 158 138 200 21 69 227 205 149 32 147 75 236 105 42 124 5 216 39 63 181 206 15 178 192 98 222 11 78 146 164 123 8 101 183 70 103 204 189 18 61 168 186 16 207 29
The diagram shows that an ICE-style bit swap has been added, between two nonlinearity phases. This bit swap is the reason that the Feistel rounds in the right half have been reversed, so that a simple bit swap between the right and left halves of the cipher moves a bit from entering the half first to be modified to entering the half first to be an f-function input.
Thus, the block cipher consists of the following steps in order at the beginning:
The exchange keys used to control the bit swap phases are processed through a 4 of 8 code, so that each bit swap phase always exchanges exactly four bits between corresponding bytes.
Note that only interchanging S-boxes S6 and S7 is required to make the lesser diffusion phase its own inverse, exactly as an S-box interchange did so for the Quadibloc 2002A diffusion phase.
Because the cipher begins with a bit swap phase, which is keyed, the cipher, on the one hand, can be combined with either an S-box or XOR whitening without waste, and on the other, it creates uncertainty about which portion of the algorithm any bit will enter; each bit may be directed towards either of the two halves of the initial Feistel rounds in the first greater diffusion phase.
This cipher includes eleven rounds of this type. In the middle of the cipher, there are three rounds, with the structure:
and at the end of the cipher there are four rounds, such that the sequence of phases is the exact reverse of that at the beginning of the cipher, and thus the subkeys used in the last four rounds are LK15 through LK22, EK9 through EK12, and K129 through K192.
Note that in the reversed rounds, the order in which S1 and S2 are used is also reversed, again in order to retain the self-inverse property of the cipher. This means that S2 is used twice in a row in the symmetric augmented sixth round; however, as there is a diffusion phase between the two occurrences, this does not seem like a serious problem.
The operations in the rounds, and their precise definitions, are as follows:
In the bit swap phase, the 128-bit block is considered as being composed of a 64-bit left half and a 64-bit right half. A 64-bit exchange key is applied to the block in this phase. Where a bit of the exchange key is a zero, the corresponding bits of the left and right halves of the block are unaffected. Where a bit of the exchange key is a one, the corresponding bits of the left and right halves of the block are exchanged.
In this phase, the 128-bit block is considered as being composed of sixteen 8-bit bytes. Each byte is replaced by its substitute in the self-inverse S-box S1 given above.
In this phase, the 128-bit block is considered as being composed of sixteen 8-bit bytes. Each byte is replaced by its substitute in the self-inverse S-box S2 given above.
In this phase, the 128-bit block is modified by being XORed with the 128-bit long subkey for the phase.
In this phase, the 128-bit block is considered as being composed of sixteen 8-bit bytes, and these bytes are also taken in pairs for some operations.
First, the first (or leftmost) four pairs of bytes are subjected to a modified Pseudo-Hadamard transform, as follows: the byte on the left is modified by having added to it, by means of modulo-256 addition, the substitute in key-dependent S-box SB3 of the byte on the right, and then the byte on the right is modified by having added to it, by means of modulo-256 addition, the substitute in key-dependent S-box SB3 of the byte on the left.
At the same time, the last (or rightmost) four pairs of bytes are subjected to a reversed modified Pseudo-Hadamard transform, as follows: the byte on the right is modified by having added to it, by means of modulo-256 addition, the substitute in key-dependent S-box SB3 of the byte on the left, and then the byte on the left is modified by having added to it, by means of modulo-256 addition, the substitute in key-dependent S-box SB3 of the byte on the right.
Then the sixteen bytes of the block are interchanged, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
4 1 2 3 8 5 6 7 10 11 12 9 14 15 16 13
Then, the first four pairs of bytes are subjected to a modified Inverse Pseudo-Hadamard transform, as follows: the byte on the right is modified by having subtracted from it the substitute in key-dependent S-box SB4 of the byte on the left, and then the byte on the left is modified by having subtracted from it the substitute in key-dependent S-box SB4 of the byte on the right.
At the same time, the last four pairs of bytes are subjected to a reversed modified Inverse Pseudo-Hadamard transform, wherein the byte on the left is the first to be modified, having the substitute of the byte on the right in key-dependent S-box SB4 subtracted from it, and then the byte on the right is modified by having the substitute in key-dependent S-box SB4 of the byte on the left subtracted from it.
Then the sixteen bytes of the block are subjected to a matrix transpose, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
so that they shall lie in the order
1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16
Then the eight pairs of bytes are again subjected to modified and reversed modified Pseudo-Hadamard transforms, as previously.
Then the sixteen bytes of the block are interchanged, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
2 3 4 1 6 7 8 5 12 9 10 11 16 13 14 15
Finally, the eight pairs of bytes are again subjected to modified and reversed modified Inverse Pseudo-Hadamard transforms, as above.
The structure of the Greater Diffusion Phase is identical to that of the Lesser Diffusion Phase, except that the Pseudo-Hadamard transforms are replaced by operations which consist of four Feistel rounds.
Also, each greater diffusion phase makes use of 32 subkeys, each one 32 bits long.
The first operation uses the first eight of the subkeys required for the phase. The subkeys are applied to the eight pairs of bytes in order from left to right, one to each pair.
The first four pairs of bytes are enciphered as follows:
The byte on the right is modified by having added to it, by modulo-256 addition, the substitute in key-dependent S-box SB1 of the XOR of the first (leftmost) byte of the subkey and the byte on the left.
Then, the byte on the left is modified by having added to it, by modulo-256 addition, the substitute in key-dependent S-box SB1 of the XOR of the second byte of the subkey and the byte on the right.
Then, the byte on the right is modified by having added to it, by modulo-256 addition, the substitute in key-dependent S-box SB1 of the XOR of the third byte of the subkey and the byte on the left.
Then, the byte on the left is modified by having added to it, by modulo-256 addition, the substitute in key-dependent S-box SB1 of the XOR of the fourth (rightmost) byte of the subkey and the byte on the right.
The remaining four pairs of bytes are modified in the same fashion, except that the roles of the left and right bytes in each pair are reversed.
Then the sixteen bytes of the block are interchanged, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
4 1 2 3 8 5 6 7 10 11 12 9 14 15 16 13
Then another eight subkeys are used, and the eight pairs of bytes are modified in a slightly different manner. The first four pairs of bytes are enciphered in this step as follows:
The byte on the left is modified by having subtracted from it, by modulo-256 subtraction, the substitute in key-dependent S-box SB2 of the XOR of the first (leftmost) byte of the subkey and the byte on the right.
Then, the byte on the right is modified by having subtracted from it, by modulo-256 subtraction, the substitute in key-dependent S-box SB2 of the XOR of the second byte of the subkey and the byte on the left.
Then, the byte on the left is modified by having subtracted from it, by modulo-256 subtraction, the substitute in key-dependent S-box SB2 of the XOR of the third byte of the subkey and the byte on the right.
Then, the byte on the right is modified by having subtracted from it, by modulo-256 subtraction, the substitute in key-dependent S-box SB2 of the XOR of the fourth (rightmost) byte of the subkey and the byte on the left.
The remaining four pairs of bytes are modified in the same fashion, except that the roles of the left and right bytes in each pair are reversed.
Then the sixteen bytes of the block are subjected to a matrix transpose, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
so that they shall lie in the order
1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16
The eight pairs of bytes are again modified with the use of eight more subkeys, following the pattern of the first layer above which involved four rounds using modulo-256 addition and S-box SB1.
Then the sixteen bytes of the block are interchanged, being moved from the order
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
to the order
2 3 4 1 6 7 8 5 12 9 10 11 16 13 14 15
Finally, the eight pairs of bytes are again modified with the use of the last of the eight subkeys for the phase, following the pattern of the layer above which involved four rounds using modulo-256 subtraction and S-box SB2.
Incidentally, note that interchanging XOR with the other operation, either modulo-256 addition or subtraction, in the rounds might be reasonable, since it is no longer a question of imitating the Pseudo-Hadamard Transform when a subkey and four rounds are present; this might diversify the algebraic operations in the cipher in such a way as to strengthen it.
Next
Start of Section
Skip to Next Chapter
Skip to Next Section
Table of Contents
Main Page