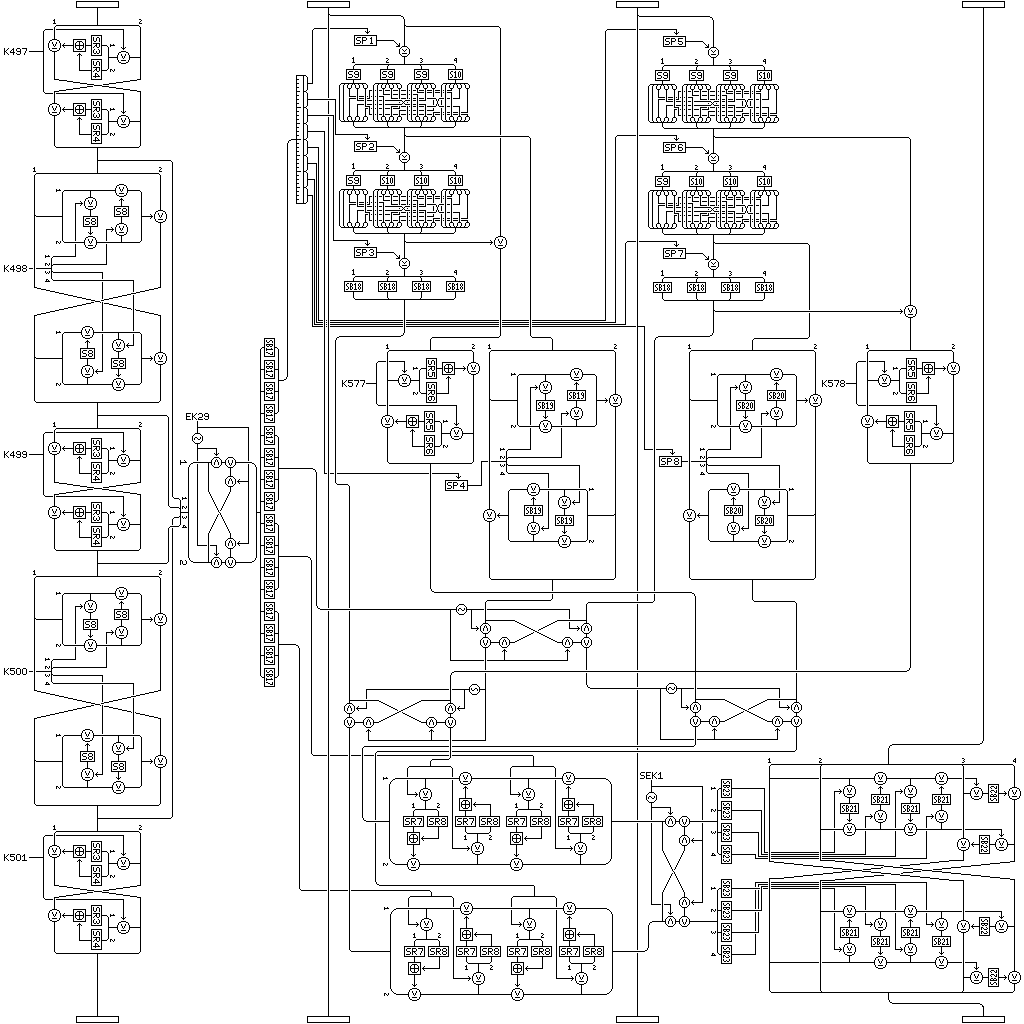
This section deals with two variants which introduce a modified form of the round used in Quadibloc 2002 to Quadibloc 2002E, since that round represented the previous attempt at a cipher of ultimate security and complexity.
Since the Quadibloc 2002E design, in its size and complexity, represents an attempt to achieve the ultimate in security in a block cipher, the fact that the design is more regular than that of Quadibloc 2002 makes it seem as if I am still, to some extent, holding back from producing the ultimate design.
Thus, the following modified version of the Quadibloc 2002 round has been designed:

so that the goal of inverting the cipher by rearranging the key schedule can still be achieved after its incorporation into a modified form of Quadibloc 2002E.
Note carefully how the inputs to the swap phase controlled by EK29 and the outputs from the swap phase controlled by SEK1 are ordered, in order to ensure that the bit swap correctly swaps between corresponding operations earlier and later in the round. Note also that S-boxes S8 through S10 are used in the cipher; these are the fixed S-boxes with those numbers generated from Euler's constant. Also, SB19 and SB20 are used in two parts of the round corresponding to parts of the Quadibloc 2002 round which both used the same key-dependent S-box instead of each using a different one. Note as well that, to preserve alternation of the direction in which f-functions operate, the small Feistel rounds using key-dependent S-boxes SR2 and SR3 operate from right to left. Also note the use of six unrestricted S-boxes with 16-bit entries, S-boxes SR3 through SR8, so as to follow the same principle as is used in the Quadibloc 2002E core rounds of using different S-boxes for each stage of the round.
It is intended that sixteen such rounds, in two groups of eight, will be added to Quadibloc 2002E to form the variant Quadibloc 2002E U (Ultimate), causing it to have the following overall structure:
Four standard rounds Eight new type rounds Four core rounds Three standard rounds Four core rounds Eight new type rounds Four standard rounds
After the first seven new type rounds in the first group of eight new type rounds, the 32-bit subblocks of the 128-bit block are to be rearranged as follows:
From the order: 1 2 3 4 to the order: 3 1 4 2
and, after the first seven new type rounds in the second group of eight new type rounds, the 32-bit subblocks of the 128-bit block are to be rearranged in the inverse order:
From the order: 1 2 3 4 to the order: 2 4 1 3
to preserve the symmetry of the cipher.
Is it possible to achieve symmetry without resorting to two different rearrangements of the block between rounds? Rearranging the block, considered as being composed of eight 16-bit parts, from the order: 1 2 3 4 5 6 7 8 to the order 6 3 2 7 8 1 4 5 would be symmetric, and at first it might seem to provide all the rearrangement required. However, in the absence of a swap of 16-bit halves of the 32-bit subblocks within the round, parts of the block, instead of going between all four subblocks, would be brought back to the subblock they came from in the next round. As it happens, for symmetry reasons, the first and fourth 32-bit subblocks do have their halves swapped by the round, but the second and third subblocks are unchanged, and thus the round would have to be significantly modified to work with this type of arrangement. However, such a modification is indeed possible, and a means of achieving it is illustrated below (and a diagram to the right illustrates the implications of this rearrangement of blocks, and demonstrates its symmetry): |
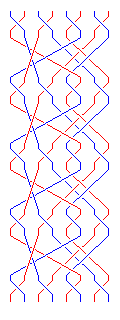 |
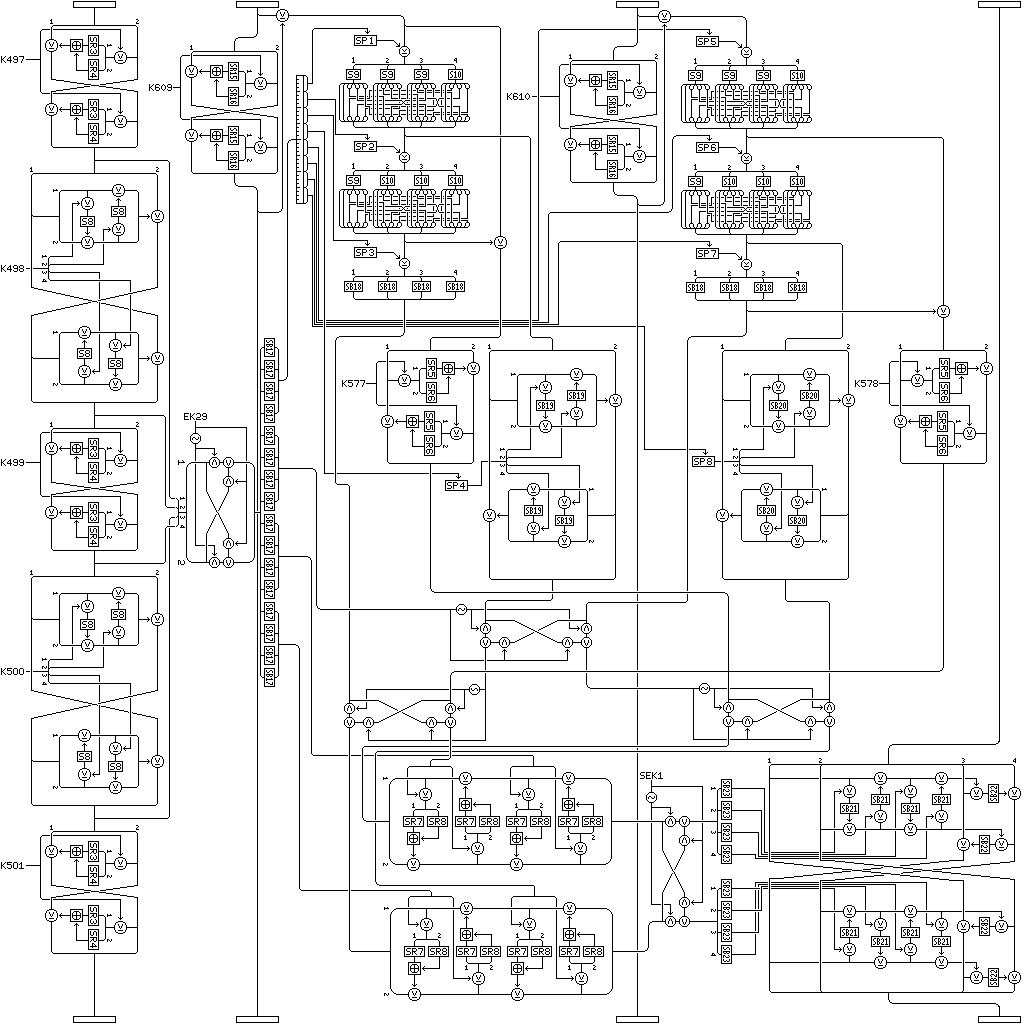
Since the new type rounds are simply added to the existing rounds of Quadibloc 2002E, the additional subkey material they require is also simply added to the Quadibloc 2002E key schedule.
The additional key material required is as follows:
This key material is generated after the key material in the Quadibloc 2002E key schedule, making the order of subkey generation the following:
For deciphering, the additional portion of the key schedule is modified as follows:
The order of subkeys K497 through K576 is reversed, and in addition the two 16-bit halves of each subkey are exchanged.
The order of groups of two subkeys within subkeys K577 through K608 is reversed, with the order of the subkeys within each group of two remaining constant.
The order of the sixteen exchange keys EK29 through EK44 is reversed, and in addition the bits of each subkey are inverted.
The order of the sixteen short exchange keys SEK1 through SEK16 is reversed, and in addition the bits of each subkey are inverted.
The order of groups of eight subkey pools within subkey pools SP1 through SP128 is reversed, with the order of the subkey pools within each group of eight remaining constant.
Modifying the round as shown above to permit a single symmetric interchange of 16-bit portions of the block between rounds results in the addition of further key material, as follows:
This key material, in that order, is added to the end of the key schedule. For decipherment, the order of groups of two subkeys within K609 through K640 is reversed. The variation shall be indicated by adding the suffix S (for symmetric) to the variation portion of the cipher name, thus leading to Quadibloc 2002E US, Quadibloc 2002EC US, and Quadibloc 2002EM US. |
Of course, given that we have previously looked at a design with a 256-bit block, how can we have an 'ultimate' cipher with a shorter block?
One way to incorporate the new type rounds into the larger block size is to take Quadibloc 2002E WS, and replace the two key phases and the greater diffusion phase in the symmetric augmented third round of each of the four parts containing five standard rounds with four new type rounds. The first two such groups of four would have the regular rearrangement of 32-bit subblocks after each of the first three rounds, and the last two would use the inverse rearrangement. The additional keys needed for the new type rounds would come at the end of the key schedule, in the same order as for Quadibloc 2002E U, giving Quadibloc 2002E WU (Wide Ultimate).
In Quadibloc 2002E WUS, since the number of new type rounds added is also sixteen, the same quantity of key material is added at the end of the key schedule; in this case, the new 32-bit subkeys would have the designations K465 through K496.
Next
Start of Section
Skip to Next Chapter
Table of Contents
Main Page