Not everyone who uses encryption is a computer programmer. People using computer programs (such as PGP) or cryptographic hardware to perform their encryption are, to a certain extent, trusting their supplier. There are possibilities for malicious alteration of an encryption system so that it seems to be functioning normally, but will reveal all your messages to the attacker who provided you with a program or device that was tampered with (while still keeping them secret from other parties).
As an example, let us take a program like PGP. How could a malicious programmer use the available source to produce a modified version of the program that would appear to operate normally in every way?
When performing conventional encryption, opportunities for mischief are few; but a modified program could hide an encrypted version of the key used, and the name of the file it was used on, somewhere on the user's hard disk.
When used for communications with both RSA and IDEA, however, there are many opportunities for mischief. (Of course, the current version of PGP uses Diffie-Hellman and Triple-DES instead, but I will avoid confusing complications.)
An encrypted E-mail message, being encrypted in CBC mode, includes an initialization vector, chosen at random by the program. This IV could be chosen to include information about the session key.
For example, the session key could be generated from the IV. Having only 2^64 possibilities for the 128-bit session key, out of 2^128, would be hard to detect.
Of course, that only lets the adversary read messages from the person who has the modified program. What about the messages to him?
Well, it is possible to do even worse. A tampered-with version of PGP could generate only 32 random bits, and combine them with 32 bits that contain both a part of one of the user's private keys, and an indication of which part of which key it is; encipher that for use as the IV, and then use the IV to generate the session key.
The method used to protect users of PGP against this is simple enough: the official version of the PGP executable was itself signed using PGP.
As a Canadian, able to distribute source code under more favorable restrictions than U.S. citizens, at least prior to a recent liberalization of the regulations, but still limited by U.S. law for executables I produce on compilers that come from the U.S., I have considered the question of whether I could make a program similar to PGP but which would have inherent resistance to tampering, by changing the protocol used, so that people using such a program, despite my having no control over the executables, would have some chance of safety.
I have recently learned that the technique which the following paragraphs describe may be covered under one or more U.S. patents, including patent number 5,673,319, owned by IBM, covering inventions by Mihir Bellare.
If one uses RSA as the public-key component of such a cipher (at the rate I'm going, the patent [on RSA, that is. The Bellare patent dates from 1997.] will expire before I write any code) one can save bandwith as well as improve security by the following expedient: instead of padding the session key with "random" bits to create a block for encipherment under RSA, encipher the following under RSA: the session key, the IV, and as much of the message as will fit. Then, the remainder of the message is enciphered using a conventional cipher system outside the RSA block.
A malicious programmer could still have the program choose several different values for the IV and session key, encrypt each one under RSA, and choose to use the one that had the desired value for a small number of bits to be leaked in the RSA block. This would be very slow; but one could instead choose different values so as to leak information in the conventionally-encrypted portion of the message, and the trials for this would be much faster. Also, even if no information is leaked, if the number of possible session keys were limited to some small value, say 2^40 or less, then (the conventionally-encrypted portion of) messages could be read without any leaked information.
So, I've taken this idea, which seems to help matters, and advanced another step with it. I propose to allow a program which, like RIPEM or PGP, encrypts messages with a combination of public and private key methods, to function without generating any random numbers whatever.
Of course, random numbers are still used to set up an initial choice of RSA keys, and so a modified program could be designed to choose primes from a set with only 2^40 members. So, 100% security is still not obtained.
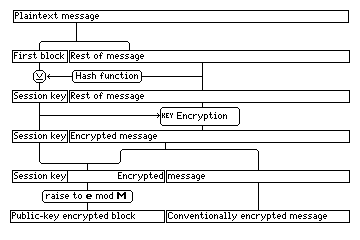
What I would do is this: Given the message to be transmitted, I would divide it into two parts: the first 160 bits, and all the rest. Then, I would obtain a 160-bit hash of the rest of the message, using SHA. This hash would then be XORed to the first 160 bits of the message. The result would be used as the session key and IV. (If 160 bits aren't enough, I would simply take the remainder of the message, and repeat the process, dividing it into a first 160 bits and all the rest.) Then, the rest of the message (whether or not it will be later part of the RSA block; this will make chosen-plaintext attacks more difficult) is encrypted conventionally. Finally, as much of the message as possible, including of course the entire session key and IV, are encrypted in a block using RSA.
The following diagram illustrates the process:

If the user needs to encrypt multiple copies of the same message, the user can manually add some random text to the message to prevent the multiple copies from enciphering identically.
If one is using hardware for encryption, other possibilities present themselves. A simple DES chip can have its operation validated; the only bad thing it can do is disclose keys when sent some secret combination of signals.
But one unusual possibility bears noting.
Suppose one is supplied with a chip (or a program) that merely carries out an unknown encryption algorithm. Obviously, there is the hazard that this algorithm might be poorly designed, and therefore weak. But there is a way to maliciously design an algorithm that would appear and be strong, except against attacks by those who set it up.
Let us suppose the following "super-duper algorithm" is provided: encryption using DES under a constant key, XOR with the key provided by the customer, encryption using DES under another constant key.
This algorithm would behave like a secure block cipher with a 64-bit key. However, to those who designed it, knowing the constant keys used for the DES steps, it would fall trivially to a known-plaintext attack.
Computer operating systems are, of course, susceptible to many kinds of attacks, such as from computer viruses, or, in the case of multi-user systems, other users exploiting weaknesses in programs that have operating system privileges. So the idea of having encryption performed by a self-contained module, which generates its own random keys without disclosing them, is attractive.
However, if one doesn't trust a hardware box not to choose keys badly, it seems one can't take advantage of this.
I've worked out a scheme by which this sort of problem can be avoided.
In addition to carrying out the steps in a secret-key algorithm such as Rijndael, let us suppose our all-in-one chip can generate random numbers in hardware, perform the multiprecision arithmetic for the RSA and Diffie-Hellman public-key ciphers, and even search for large primes. Let the chip have its own public/private RSA key pair for communicating with the outside world.
Then, I propose to have the chip function in the following way: when requesting it to encipher data using its secret-key algorithm, send it a block of random data from which to produce the key to use. How the key is derived from the data is known. The data is encrypted using the chip's public RSA key.
Thus, one can generate one's own data block, calculate the hash, and encrypt the block, and then one can check that the chip, like any other chip for simply performing a secret-key cipher, is encrypting the data correctly with that key.
But the chip can also generate blocks of random numbers from internal hardware. Instead of using them directly as keys, it encrypts them using its own public RSA key, and provides the user with the result.
The computer in which that chip is installed can then use that random data as a starting point, applying a randomly chosen transformation to it. The result is a block of data, still encrypted in the chip's public RSA key, whose decrypted value is not known to the computer, but which is effectively random from the point of view of the chip, which can no longer recognize it as a key it produced.
In this way, as long as the software carrying out encryption, and the chip, were not produced by groups that could collude, one is not required to fully trust either the chip or the computer software. Of course, the computer software still handles plaintext, but that would be true using an ordinary encryption chip as well; this simply allows the benefits of an all-in-one encryption chip to be obtained from a chip that doesn't need to be trusted.
Further steps are needed to complete this, at least in many applications. The encrypted random blocks from the chip need to come with signed certificates, so that the user can, after an altered block was used for encryption, reveal the original block used and the transformation applied to it, and get a signature from the chip that a particular stream of data was encrypted with a chip-generated key. This ensures other parties to a communication that rogue software on one computer wasn't bypassing the random key generation feature of its chip.
Searching for primes to produce a public/private key pair would also use a random seed block of the same form as used for a secret key; here, once the key pair was produced, one can reveal the source of a seed block to obtain a similar certificate.
The transformation I propose is raising the random block to a randomly chosen power, modulo the RSA modulus in use.
Multiplying the block by a number, as is typically used in blinding schemes, can't be used, though.
What is required of the key is that neither the chip, nor the operating system, can control its value. Because discrete logarithm is hard, the operating system, when given a random value by the chip, can't find an exponent that will produce a desired value (in this case, the desired key, encrypted using the chip's public RSA key) as a result.
In the case of multiplication as a blinding method, the blinding factor required to produce a desired value can be determined through modular division, so no assurance would be obtained that the operating system does not know, and did not directly choose, the key, from the fact that it is a blinded version of a chip-generated key.
But more general transformations, like a one-way hash of the key, subject to rules that kept the result in the required range, are also possible.
Also, it's been noted that this scheme can be improved by having the user choose a blinding exponent in advance, and supply a hash of it when requesting a random block, thereby preventing searches by the software for a blinding exponent with special characteristics. This may well be important for some applications.
The one-time pad is well-known as the one perfect cipher. If one uses a genuinely random method, such as rolling dice, to generate a key as long as the message you will encipher, and you use it only once, you can have perfect secrecy.
There are detailed conditions that must be met. You can't use a ten-digit key to encipher ten letters in the Gronsfeld cipher, nor can you use ten digits to encipher ten digits by addition, and then transmit a twenty-digit ciphertext that includes the carry digits, and still have perfect secrecy.
If there are N possible plain messages, there must be at least N possible keys, and exactly the same N (or more) possible cipher messages must be possible for each plaintext message. The "or more" notes that it isn't necessary, for example, to compress a text message perfectly before encrypting it with a one-time pad.
Supposing, though, that one were using one-time pads to encipher plain-language text in Vigenere. And you randomly generated a one-time pad with a long stretch like AAAAAAAAAAAAAAAAAAAAAAAAAAA in it. Applying that pad to the plaintext results in a stretch of plaintext appearing in the enciphered message. But throwing all such pads away means that we have *fewer* than N possible keys, so messages DO contain information about the underlying plaintext, whereas before they didn't, but they only appeared to.
What are you going to do?
One can be practical. In the real world, pads with stretches of more than, say, five A's in a row, or six of any other letter in a row, are such an infinitesimal fraction of the possible one-time pads, that throwing them away would not necessarily compromise security seriously. Emotionally, sending a message enciphered by the occasional pad with a long stretch of As seems like sacrificing one message to preserve the security of other messages: and if lives depend on the messages, to sacrifice a specific person's life to protect the general security of a system is not in accordance with our society's moral values.
And, of course, physical random-number generators can experience mechanical failure. A long stretch of As may be a symptom of it, but it is not always possible to verify whether or not a failure has taken place, to determine if a long stretch of As is a systematic error or a legitimate random event.
But let us suppose that our plaintext was enciphered securely using a conventional method prior to applying the one-time pad. Then a pad of all zeroes would not be as big a problem; the text would still be protected.
Also, if the encryption was done in the domain of digits from 0 to 9, we would not even have the problem that a securely-enciphered message might be enciphered by a one-time pad that, by an incredible coincidence, produced a ciphertext which expressed the information in the plaintext. Digits are just digits; a sequence of them (generally) has no (predefined) semantic content. It's just a bunch of numbers, it doesn't mean anything! So one has no problem with a one-time pad accidentally putting a naughty word in the ciphertext, which is more likely than accidentally revealing your secret message.
One way to deal with the problem of undetected mechanical failures in random-number generation would be the following: use a randomizer with 27 positions to generate values, and always discard any value which matches the preceding value. This leads to 26 possible values not being discarded, and so a one-time pad of letters can be formed whose repetitions are guaranteed not to be due to a mechanical failure.
There is the technique of Peres unbiasing which is related, but which deals with bias in the proportions of individual values, while this technique assumes no bias, but instead deals with the correlations between values.
It isn't immediately obvious how to combine the two techniques, since applying one technique seems to destroy the identity of the different values needed to apply the other technique. But the techniques can be combined; one crude way would simply be to generate twice as much random material as is required, and then combine together two sequences, one of which had undergone the one process, and the other which had undergone the other process. This, however, is indeed crude and does not really result in a sequence provably free of bias and correlation.
To get rid, however inefficiently, of both bias and correlation, one could do the following:
Given an initial sequence of physically random bits, take them in pairs, and use 01 to generate 0 in the second level, and use 10 to generate 1 in the second level.
Then split these bits into the bits which followed a zero and the bits which followed a 1. Subject each group of bits to unbiasing separately; here, full Peres unbiasing can be used for more efficiency.
One could improve the efficiency by using Peres unbiasing in the first step, but then taking the output bits from each possible portion of the unbiasing tree separately when it comes to splitting the bits into those preceded by a 0 or by a 1. Doubtless, there have been published papers on this sort of thing in the literature.
Finally, we are coming to the reason why this topic is being discussed here instead of on some other page.
As noted above, if one securely enciphers one's text before applying a one-time pad, then one might feel more serene in using a pad that contained all zeroes.
One could do this by using a stream cipher. But then the one-time pad might invert the stream cipher by coincidence.
One could do this by using a block cipher. Perhaps one round key in Rijndael, or a consecutive pair of subkeys in DES, could be supplied from the one-time pad. But then a one-time pad of repeated blocks would degrade the encipherment somewhat, since it would no longer change with each block.
To avoid these dangers, and to make malicious creation of a one-time pad impossible even in principle, in a USENET post I suggested enciphering each message block with a block cipher, and supplying two round keys in that cipher from a secure stream cipher method, as well as supplying one from the one-time pad.
If you use a stream cipher, though, you need an initialization vector. That is generated locally from a random source, not from a prearranged source of one-time pads, since it is included with messages in the clear.
An elaborate method was noted above for using all-in-one encryption chips to generate physical random values without trusting them. In the post under discussion, I assumed the random source was reasonably trustworthy, and so I came up with something less elaborate. The random source generates a random value, which can be viewed by the encipherer. The encipherer then types some random characters on a keypad, and the random value and the keypad characters are then combined using a secure one-way hash function, in a deterministic fashion which can be checked and validated externally, to produce the initialization vector.
This is not perfect, since "random" characters punched on a keypad have patterns, and so one could still leak keys by exploiting this nonrandomness, but as long as the hash function used is secure it would work.