A rotor is a small disk of insulating material, with perhaps 26 equally-spaced electrical contacts in a circle on each side. The contacts on one side are connected to the contacts on the other side in a scrambled order.
In Hebern machines, the contacts on the rotors were simply flat circles of metal; the machine had ball contacts on springs to make contact with them. This allowed the rotors to be put in upside down, for more possible keys. The Enigma, on the other hand, was built more cheaply; the rotors had plain metal contacts on one side, and spring contacts on the other. This almost halved the number of contacts needed, provided you didn't decide to use a new set of rotors.
A rotor provided a changing scrambled alphabet, by (you guessed it!) rotating. A rotor with 26 contacts on each side, each corresponding to a letter of the alphabet, that changed E to M before rotating would now change D to L (or F to N, depending on the direction in which it rotated), while E could become any other letter, depending on the way the different wire went that was now brought into position to encipher it.
Thus, while one might use a slide like this to perform mixed-alphabet Vigenère encipherment:
----------------------------
| plhzctyqjufebsiwmvnkadxrog |
------------------------------------------------------
NDXFPZATLCRVGQOBKMYJIHUESWNDXFPZATLCRVGQOBKMYJIHUESW
------------------------------------------------------
where a plaintext letter in the top row is taken directly to a ciphertext letter below it, a rotor machine behaves like this kind of slide:
------------------------------------------------------------------------------
| a b c d e f g h i j k l m n o p q r s t u v w x y z |
---------------------------------------------------------------------------------------------------------------------
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 1 2 3 4 5 6 7 8 9 10 11 12
22 17 9 26 12 21 8 15 3 25 10 19 14 2 16 6 1 18 24 11 7 23 4 20 5 13 22 17 9 26 12 21 8 15 3 25 10 19
---------------------------------------------------------------------------------------------------------------------
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
------------------------------------------------------------------------------
or (particularly for Mac users, for whom fonts of the same size have fewer dots):
----------------------------
| abcdefghijklmnopqrstuvwxyz |
------------------------------------------------------
11111111112222222 11111111112222222
1234567890123456789012345612345678901234567890123456
21 212 1 2111 1 121 2 2 121 212 1 2111 1 121 2 2 1
2796218535094266184173405327962185350942661841734053
------------------------------------------------------
| ABCDEFGHIJKLMNOPQRSTUVWXYZ |
----------------------------
where a plaintext letter first becomes the number below it, and then that same number, in the second row of numbers, becomes the letter below it. Thus, when the central slide is moved, the random scrambling of the alphabet is applied to different plaintext letters as well as producing different output letters, with both displacements the same (or, in another sense, equal and opposite).
Note that the example given had the rotor moving "backwards" by default. If the rotors are labelled with letters going in the same direction as the use of the input contacts, and they advance so that the next letter in the alphabet becomes visible at a fixed position, the result will be to move the contacts on the rotor to the input contacts corresponding to the previous letter from the ones to which they were previously connected.
The five rotors on a Hebern machine came close to moving like the wheels of an odometer. However, they did not move precisely in this way. There were fast rotors, which moved once for every letter enciphered, medium rotors, which moved once for every 26 letters, after a carry from the fast rotors, and there were slow rotors, which moved once after 650 (rather than 676) letters were enciphered. And there could also be rotors that didn't move at all, except that they could be set by hand before encipherment began. Some versions of the five-rotor Hebern machine had control levers, which determined which rotors moved each way.
The 'carries' between rotors were handled by ratchet gears that were at the two ends of the shaft carrying the rotors. The reason for the slow rotors moving after every 650 letters was because the machine was designed to avoid having the slow rotor moving at exactly the same time as the medium rotor, since having all the rotors move together seemed like a weakness.
A good picture of a Hebern rotor machine appears in the July, 1966 issue of Scientific American, which has an article on cryptology by David Kahn.
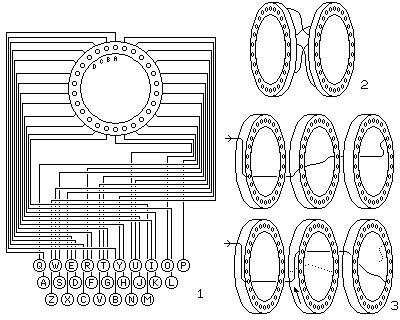
The following diagram may illustrate a little about how a rotor machine works:

In the first section, we see the keyboard connected to a set of contacts, arranged in a circle, forming the input to the first rotor. Often, the contacts are arranged so that the contacts on the circle are in alphabetical order; the early commercial Enigmas were wired so that the contacts matched the keyboard arrangement instead.
In the second section, I attempt to illustrate that the contacts on both sides of a rotor are connected so that each contact on one side is connected to one contact on the other side, but in a scrambled way.
In the third section, I follow the fate of the letter E through three rotors, before and after the one in the middle advances one step. The path of electricity through the first rotor stays the same; but the movement of the second rotor has brought a second wire into contact with the electricity; the wire formerly used is shown as a dotted line in its new position. The third rotor has not moved, but since the electrical current has left the second rotor from a different contact, a different wire in that rotor is used also, the old one also shown as a dotted line, but this time in the same position.
One late rotor machine design that has become known to the public is that of the Hagelin HX-63, which was offered for sale in the early 1960s, but was quickly phased out by electronic cipher devices.
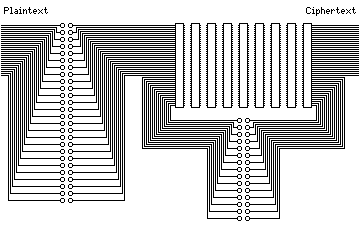
It had nine rotors, each with 41 contacts. As it enciphered a 26-letter alphabet, wires looped 15 of the rotor bank's output contacts back to its input.
There were two plugboards with the machine; one scrambled the 26 plaintext letters on input, and another scrambled the 15 loopback connections. (It is somewhat surprising that a plugboard scrambling the plaintext on input was chosen over one scrambling the ciphertext on output: it would seem the latter would provide better protection against cryptanalysis, for the same reason that a Type II slide is to be preferred over a Type I slide.)
The following diagram illustrates the wiring of an HX-63, showing the wires that are looped back and the plugboards:
It is described as having a "very irregular" motion of the rotors, and each rotor had a set of 41 switches the setting of which would vary the effective wiring of that rotor.
Although I do not know what wiring scheme was chosen for those switches, one possibility might be something like this:

The alphabets produced by a single rotor in its various positions can be shown in a tableau similar to those used for Vigenere; such a table would look like this:
Rotor
position Plaintext
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
-----------|-----------------------------------------------------
A | L N K Y U W Z J X H E I A O G S P V C T D R B Q F M
B | M J X T V Y I W G D H Z N F R O U B S C Q A P E L K
C | I W S U X H V F C G Y M E Q N T A R B P Z O D K J L
D | V R T W G U E B F X L D P M S Z Q A O Y N C J I K H
E | Q S V F T D A E W K C O L R Y P Z N X M B I H J G U
F | R U E S C Z D V J B N K Q X O Y M W L A H G I F T P
G | T D R B Y C U I A M J P W N X L V K Z G F H E S O Q
H | C Q A X B T H Z L I O V M W K U J Y F E G D R N P S
I | P Z W A S G Y K H N U L V J T I X E D F C Q M O R B
J | Y V Z R F X J G M T K U I S H W D C E B P L N Q A O
K | U Y Q E W I F L S J T H R G V C B D A O K M P Z N X
L | X P D V H E K R I S G Q F U B A C Z N J L O Y M W T
M | O C U G D J Q H R F P E T A Z B Y M I K N X L V S W
N | B T F C I P G Q E O D S Z Y A X L H J M W K U R V N
O | S E B H O F P D N C R Y X Z W K G I L V J T Q U M A
P | D A G N E O C M B Q X W Y V J F H K U I S P T L Z R
Q | Z F M D N B L A P W V X U I E G J T H R O S K Y Q C
R | E L C M A K Z O V U W T H D F I S G Q N R J X P B Y
S | K B L Z J Y N U T V S G C E H R F P M Q I W O A X D
T | A K Y I X M T S U R F B D G Q E O L P H V N Z W C J
U | J X H W L S R T Q E A C F P D N K O G U M Y V B I Z
V | W G V K R Q S P D Z B E O C M J N F T L X U A H Y I
W | F U J Q P R O C Y A D N B L I M E S K W T Z G X H V
X | T I P O Q N B X Z C M A K H L D R J V S Y F W G U E
Y | H O N P M A W Y B L Z J G K C Q I U R X E V F T D S
Z | N M O L Z V X A K Y I F J B P H T Q W D U E S C R G
This kind of table, for a rotor, is called a Friedman square.
Just as a Vigenere table has a regularity, in that it shows the same alphabet in its rows (and columns) repeatedly, only shifted, here a regularity is visible as well, but it is subtler: the diagonals of this square are shifted regular alphabets.
A powerful technique, symmetry of position, is used with polyalphabetic ciphers produced by mixed-alphabet slides. Since this table also has regularities, the same technique can be adapted to its structure.
In a mixed-alphabet Vigenere, if the letters A and B become Q and V in one alphabet, and T and R in another, then Q and V are separated by the same distance as T and R in the cipher alphabet.
In a rotor machine where the entry rotor is the fast rotor, the principle is the same, except now if the fast rotor has moved one position between the two alphabets, the comparison would be between A and B becoming Q and V in one position, and Z and A becoming T and R in the other position.
So in this case, the two mixed alphabets being considered are the one provided by the fast rotor, and the one provided by the other rotors. The shifts of the fast rotor need to be compensated for in the input. Similarly, if the output rotor were the fast rotor, the shifts would be adjusted for in the ciphertext letters.
What about the case when the input and output permutations to a rotor are both unknown? For example, when the fast rotor is in the middle of a stack of five rotors. At first, it might seem hopeless to apply symmetry of position to that case, because there seems no way to tell when an input or output in one case involves the same wire in the moving rotor or not as in another case.
But there is a way to apply symmetry of position in this case, given enough text with overlapping key settings. Incidentally, if the entry and exit alphabets of the rotor machine as a whole are known, in the case we are considering, where rotor 3 is the fast rotor, positions where rotors 1, 2, 4, and 5 are all displaced by the same amount, the known plaintext, known ciphertext, and fast rotor position can all be translated to permit including known plaintext from such a key setting for comparison.
One thing is assumed to be known, the position of the rotor being examined, which advances one step each time while the other rotors do not move.
With nearly complete alphabets, some progress can definitely be made in this case.
Another possibility does not produce certain results, only probable relationships.
Suppose that in position 1 of the rotor under study, plaintext A becomes ciphertext B; in position 7 of the rotor under study, plaintext C becomes ciphertext B; in position 11 of the rotor under study, plaintext C becomes ciphertext D; and in position 14 of the rotor under study, plaintext A becomes ciphertext D.
This creates a closed cycle of equivalents, separated by a given pattern of rotor displacements.
If we also knew that in position 2 of the rotor under study, plaintext W became ciphertext X; in position 8 of the rotor under study, plaintext Y became ciphertext X; in position 12 of the rotor under study, plaintext Y became ciphertext Z; and in position 15 of the rotor under study, plaintext W became ciphertext Z, then we might think it likely that the two structures correspond, and the same rotor wires are involved in corresponding steps of the two cases.
If so, then W precedes A, and Y precedes C, on the input side of the rotor, and X precedes B, and Z precedes D, on the output side of the rotor, by exactly one position in each case.
Since all our elementary facts about the rotors are of the form perm(e-7)=R-7, that is, a relationship between one plaintext letter and its equivalent for one particular rotor position, there is no way to directly amass equations that can be used to solve for any direct facts about the structure of the rotor as an unknown; instead, differences and patterns have to be relied upon.
Symmetry of Position is a technique that is used to reconstruct rotor wirings when a large amount of information is available about the alphabets produced by a rotor. But how does one get started attacking ciphertext produced by a rotor machine?
Let us assume the simplest case, where one knows the initial positions of the rotors for each message, and where the fast rotor is the exit rotor. However, we can allow an unknown assignment of the exit contacts from the rotor bank to the display or printer of the rotor machine, and we will assume that only ciphertext is available.
With the exit rotor the fast rotor, one has stretches, 26 letters long, where the fast rotor, in its different positions, is the only thing enciphering monalphabetically enciphered text. But each stretch deals with text enciphered in a different monalphabetic cipher, so how can that help us?
The chance that two texts, enciphered independently, will have the same letter at any given position, is 1/26. Two plain-language texts, or two texts enciphered in an identical manner by means of a polyalphabetic cipher, will have a greater number of coincidences; aligning messages on the basis of single letter coincidences is called the kappa test. But let us assume we do not have any overlapping rotor settings to help us. How can the principle of the kappa test help us?
Monalphabetically enciphered texts, even if they are not enciphered by the same monalphabetic cipher, still have one thing in common: they have an uneven frequency distribution. In English, the letter E makes up 12% of an average text, and the letter T makes up 9%. Twelve percent of 26 is just over three.
Thus, one can take our stretches of 26 enciphered letters, and compare them with each other. When we find coincidences, it is likely that the monalphabetic substitutions which provided the inputs to the fast rotor in both cases used the same letter or letters as substitutes for one or more high-frequency plaintext letters.
Thus, in the ideal case, by coincidences we might find a number of stretches with many coincidences with each other, and in each of the 26 positions in a stretch, the letter involved in the most coincidences would be the substitute provided by the fast rotor for the particular letter that, for most of those stretches, was the substitute for plaintext E produced by the rest of the rotor machine.
Since there are several high-frequency letters in English, the result is not likely to be that easily obtained; instead, there will be many possibilities, and the technique of symmetry of position, above, will be one of the things used to narrow down the possibilities.
Next
Chapter Start
Skip to Next Section
Table of Contents
Main Page