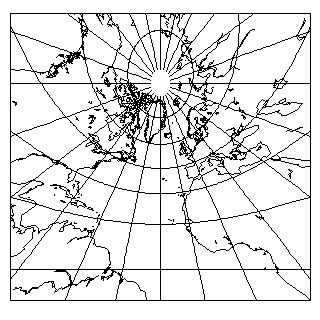
The Gnomonic projection is one which has a greater expansion, away from the origin, than a conformal projection. It gives quite a distorted apperance, therefore:

However, it has one very useful special property.
It is constructed by projecting every point on the globe appearing in the map onto the plane of the map from an imagined light source in the center of the globe. Great circles on the globe are all bands like the Equator, which are defined by planes cutting the globe that intersect the center of the globe.
Any plane intersecting a plane produces a straight line.
Hence, on the gnomonic projection, all great circles are represented by straight lines, making it very useful in plotting great circle routes between arbitrary destinations. As has doubtless often been said, it is the navigational chart for the air age much as the Mercator was the navigational chart for the age of sail.
It can also be employed fairly simply for projecting the world onto the surface of various polyhedra.
Above is a simple example, the world projected onto a cube using the Gnomonic projection.
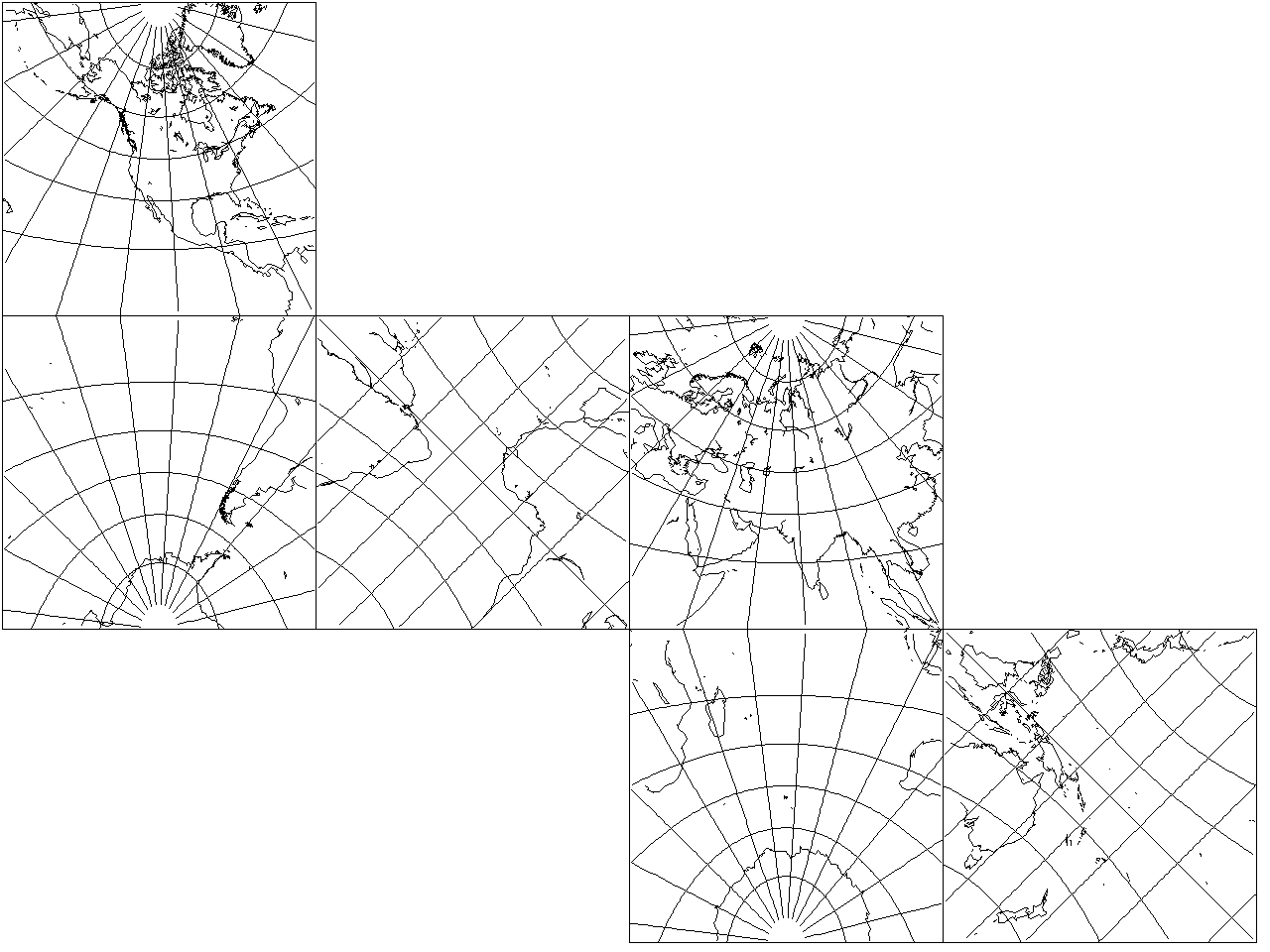
Thanks to G.Projector, I can, without too much trouble, show a more complicated example, the world projected, using the Gnomonic projection, onto an icosahedron, following the proposal of Dr. Irving Fisher from 1943 in the Geographical Journal:
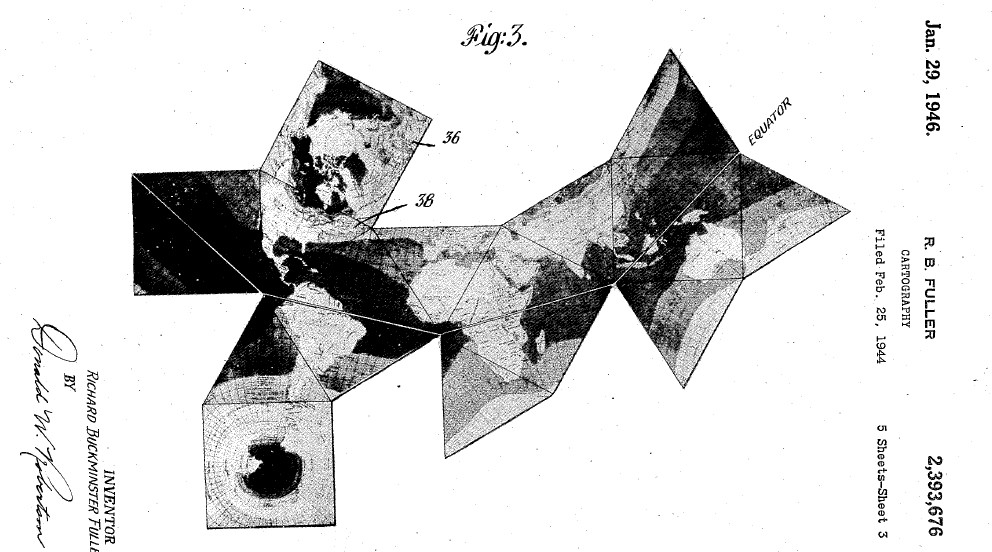
Buckminster Fuller proposed a number of inventions making use of the cuboctahedron, which shape he referred to as the "Dymaxion". This included a map projection on the surface of a cuboctahedron, which appeard in the March 1, 1943 issue of Life magazine.
I can show what it looked like from the patent for this projection:
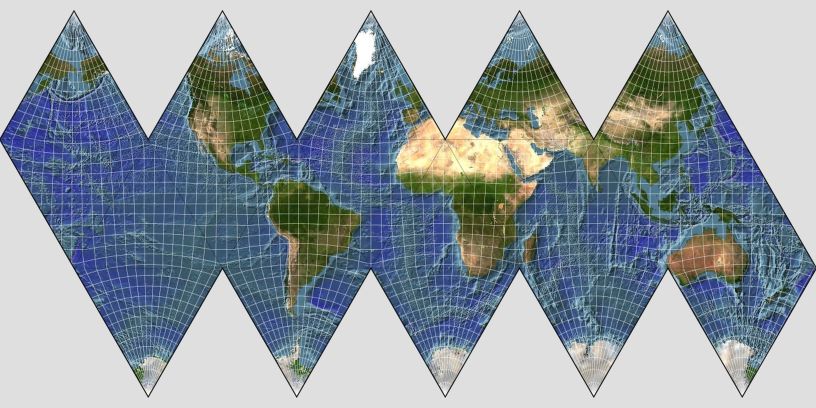
Later, in 1954, in collaboration with Shoji Sadao, he came up with a second gnomonic polyhedral projection, this one on the surface of an icosahedron. It was called the Dymaxion Airocean World.
That one looked like this, as I can show you thanks to Map Designer:
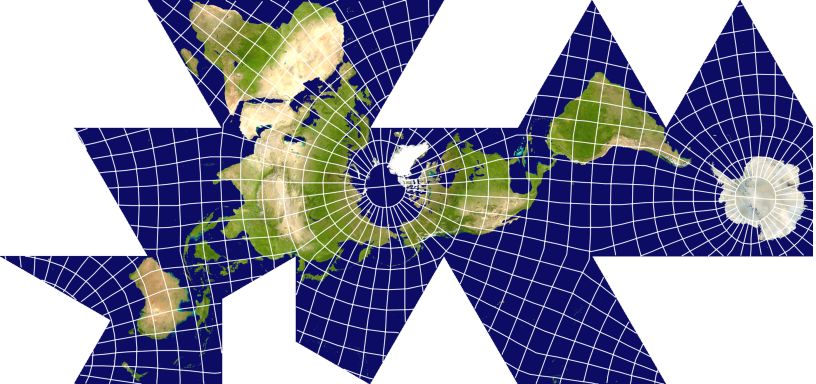
Here, it is laid out so as to avoid dividing any continents.
So one of the triangles is cut in half, and another one has a third removed from it. How this works is shown in the diagram below:
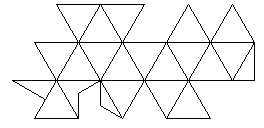
This particular arrangement of the triangles of the projection is termed the "One World Island" arrangement, as it shows the major land areas on the globe as essentially a single unit, based on the areas where the various continents approach each other the most closely.
The National Geographical Society, inspired by the game Trivial Pursuit created their own game designed to teach geography, Global Pursuit.
This game included three sets of twelve pentagonal tiles, each containing a map of the world as projected using the Gnomonic projection on the surface of a regular dodecahedron.
Using the Gnomonic projection to project the sphere onto the surface of a regular dodecahedron was one of the first such schemes to be patented, by James Addison Smith in 1939, in U.S. Patent 2,153,053.
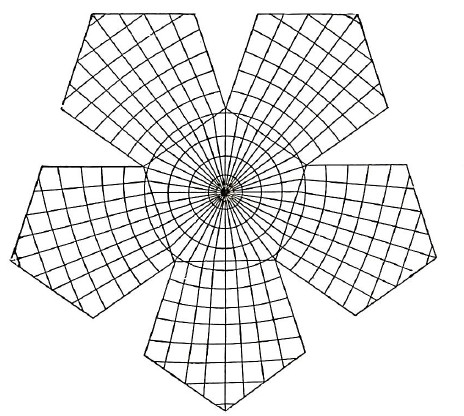
Above, from the 1928 book "A Little Book on Map Projection", by William Garnett, is what the graticule of this projection looks like.
Note that the 360 degrees of the circle are divided into forty zones of longitude, so the meridians are spaced by nine degrees in order to make the graticule symmetrical.
Since the Gnomonic has the property that all great circles are straight lines on it, and also from symmetry which means that the Equator will need to cross the outermost sides of the outer pentagons in the middle, I can unambiguously identify the Equator, and therefore see that there are also ten zones of latitude from the pole to the Equator, so the parallels are also spaced by nine degrees in this illustration.
I have now found an image of the dodecahedral use of the Gnomonic projection with the continental outlines filled in, from the April 1929 Monthly Weather Review.
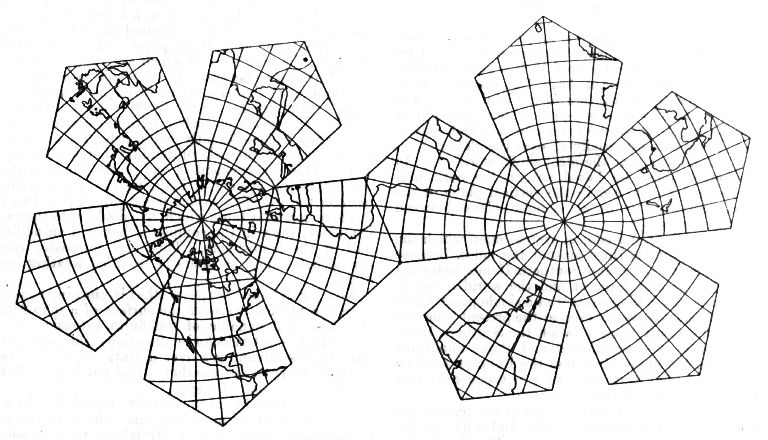
What I could access was a microfilmed version, but after retouching to correct the poor color of my source, the result doesn't seem to look too bad.
Here, the parallels of latidude are at 10 degree intervals, while the meridians of longitude are at 12 degree intervals.