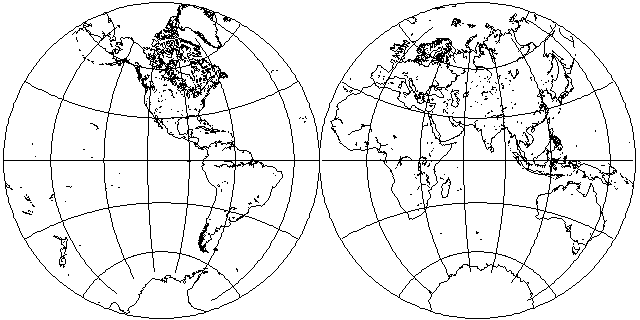
The Stereographic projection, particularly on hemispheres as shown here:

was very common on antique maps of the world, and here is an example of its use in an old atlas:
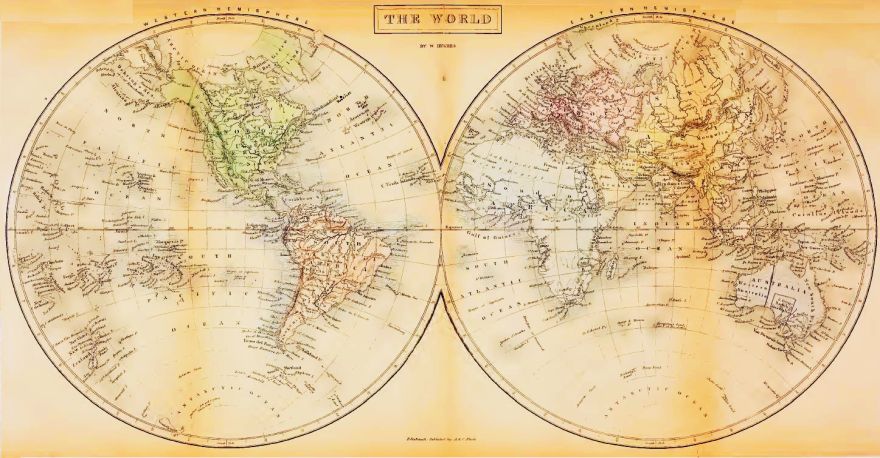
Here is another example, from the pages of the Atlas Maritimus, granted its copyright on March 22nd 1671 (1670 if you reckon the New Year from March 25th, I suppose):

This is the sort of beautiful old richly-decorated map reproductions of which are made to put on one's wall even today.
In three of the four corners of the map, there are diagrams of the Solar System, this map being agnostic with respect to one of the controversies of its time: in the upper right corner is the Solar System according to the hypothesis of Tycho Brahe, in the lower right corner is the Solar System according to the hypothesis of Copernicus... and in the lower left corner is the Solar System as Ptolemy described it.
Oh, yes: I wasn't kidding about that March 25th stuff.

It took me a moment to figure out what
70 16 -- 71
was supposed to mean, but I quickly remembered that in the past, March 25th, rather than January 1st, was considered to be the beginning of the year, and so this must have been during the transition period.
And indeed it was. March 25th was adopted as the start of a new year in England back in the 12th Century, but went back to the ancient Roman practice of starting the year on January 1st in 1752... which is also when they switched from the Julian calendar to the Gregorian calendar.
But both of these possible dates on which to begin the year were in use in England starting in 1582, and thus, March 22, 1671 does fall within that 170-year period of potential confusion.
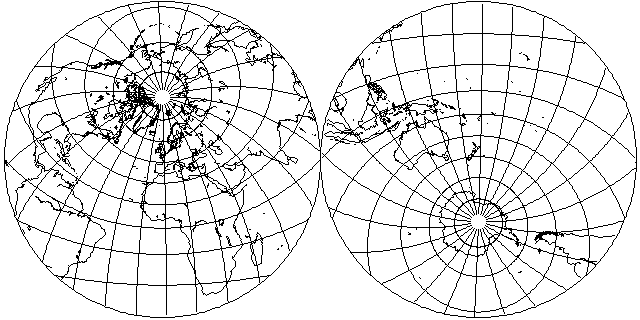
Another common use for the Stereographic projection was to present the world as "Land" and "Water" hemispheres, which here I approximate in whole degrees, centering the land hemisphere on 2 degrees West longitude and 47 degrees North latitude:
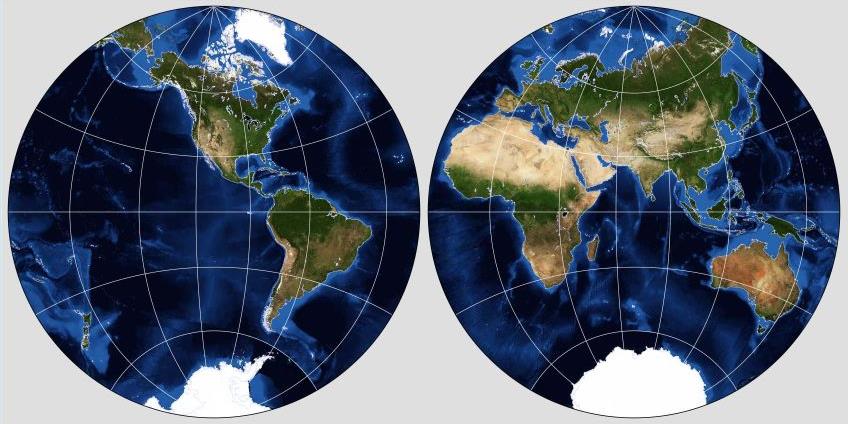
It is sufficiently important that I feel it deserves to also be depicted in a more pictorial version, as produced by the program G-Projector:
This is a map projection that was known to the ancient Greeks. Like the Mercator projection, it is conformal. In addition to being used for maps, it is also sometimes used in crystallography.
It has the interesting and unusual property that all circles on the globe, small or great, appear as circles on the projection. This simplifies drawing it.
The Stereographic is constructed by projecting the globe onto a tangent plane from a "light source" located at the point on the globe antipodal to the plane's point of tangency - the spot where the plane on which one is drawing the map touches the globe.
The following diagram:
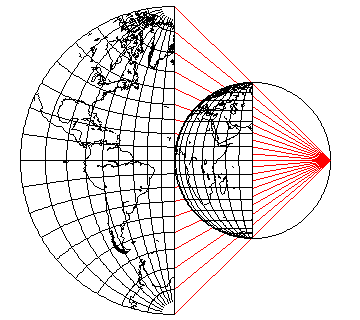
illustrates this principle.
Why is the Stereographic projection conformal?
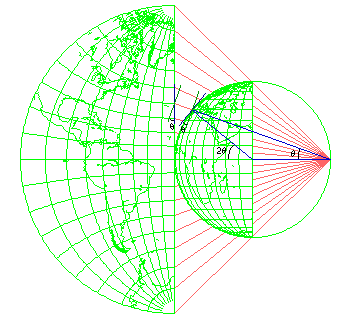
This diagram reveals the reason.
The line going from the center of the globe to a point on its surface makes twice the angle that the line of projection does from the normal to the center of the projection. This is because an isosceles triangle is formed, having two equal arms, one from the center of the globe to the projection point, and one from the center of the globe to the location on the globe being placed on the map.
Because of that, the angle the surface of the globe makes to the line of projection, and the angle the surface of the map makes to the projection, are the same, although in opposite directions, and so the foreshortening of both from the viewpoint of the projection ray is the same.