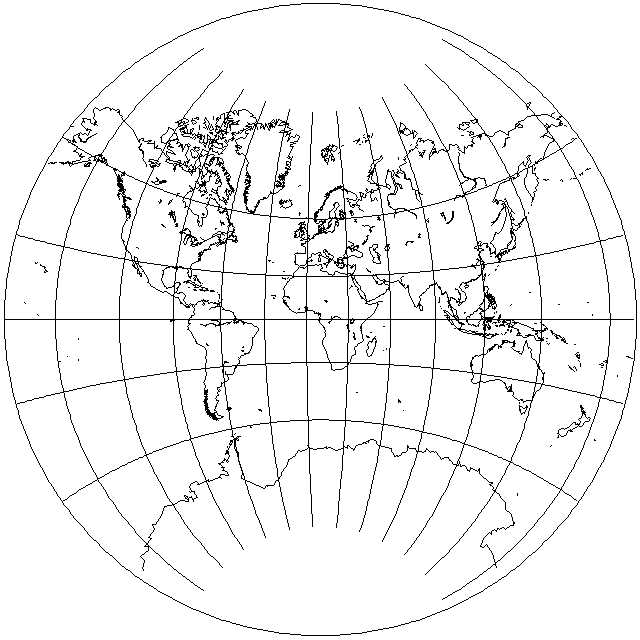
This is a conformal projection of the Earth on a circle, except that angles are halved at the poles instead of being faithful there.

It might easily be mistaken for the Van der Grinten projection, but this projection is actually conformal, and is not merely a conventional projection as the Van der Grinten is:
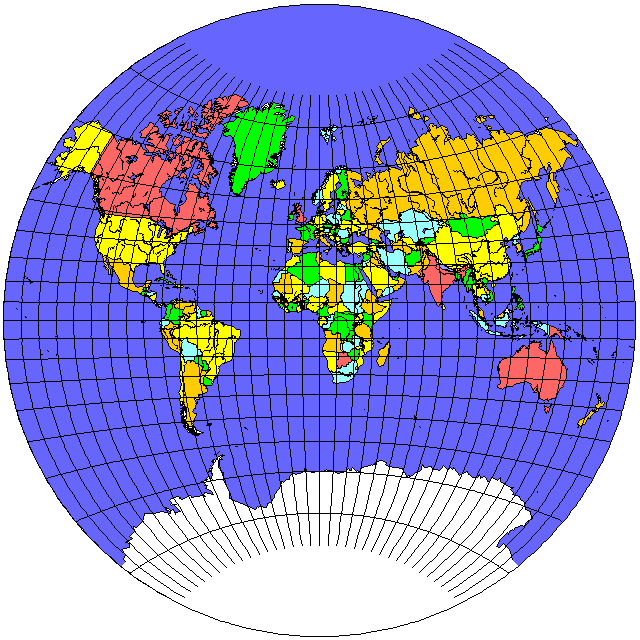
One way to tell them apart is to note that the spacing between the meridians increases towards the sides of the map. Given that change in spacing, perhaps a map based on this projection might be more useful if it placed the Pacific Ocean in the middle of the map, so that the parts likely to be of the most interest were drawn on a larger scale:
The way in which this projection was derived can be explained in a simple way without too much mathematics.
The trick behind it is this:
Take two Mercator maps, one at exactly half the scale of the other. Copy the smaller one onto the larger one, with them aligned so that their equators coincide.
Now, using the larger map to guide the relationship between each point and the globe, copy the traced version of the smaller map to the globe. It will only fill one hemisphere of the globe, since the smaller map is half as wide as the larger map.
Make a stereographic projection of the image of the smaller map on the globe.
This diagram may help to illustrate the procedure:
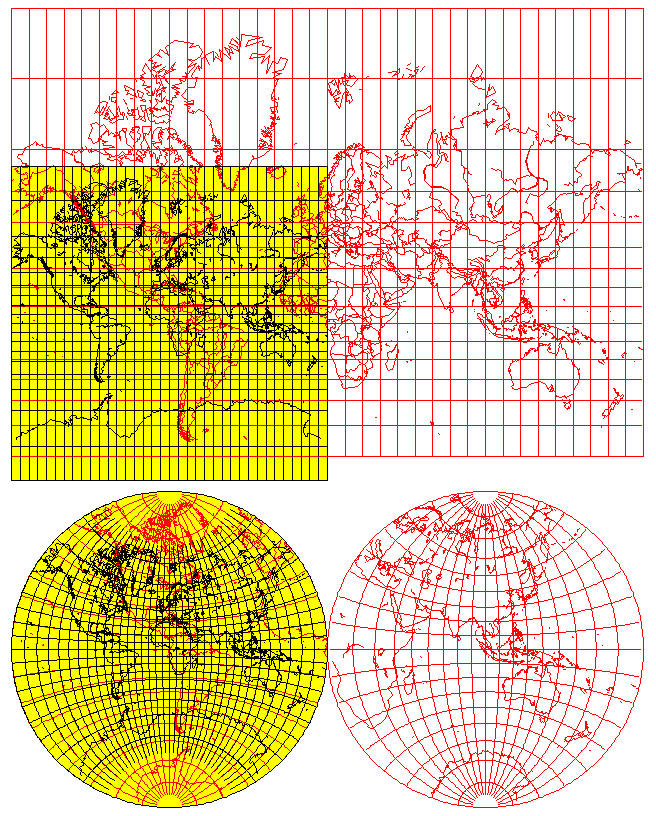
Since each of the mappings performed along the way was conformal, the sum total of all of them is conformal as well, because angles were preserved every step of the way.
Instead of having the smaller map one-half the size of the larger, one can make other choices. So if the smaller map is two-thirds the size of the larger map, one can produce this attractive conformal projection:
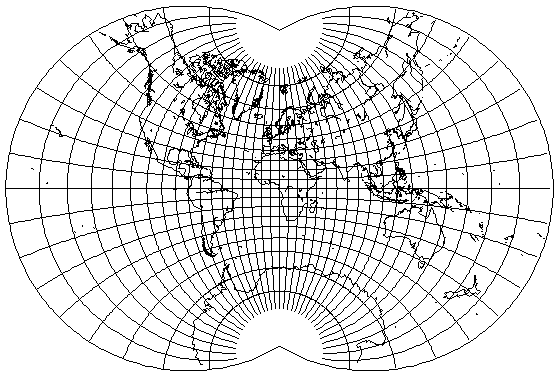
Note that the point at the poles is not conformal; unlike the August conformal on the next page, the poles are not cusps with a full 360 degrees immediately around them; instead, only 240 degrees are available to the poles, so just as in the Lagrange projection to a circle, the poles are points where the projection is not conformal.
What appears to be a somewhat similar projection, but based on reducing the starting Mercator map to a size slightly larger than half the size of the one on which it is placed, is noted on the web site of the famed musician Wendy Carlos, who is well remembered for the popular album "Switched-On Bach".
The idea of conformally mapping the globe to half of itself, the basic step which allows this projection to be produced, was referred to in a Mathematical Games column by Martin Gardner in Scientific American magazine on unusual map projections, where the final step of copying from the globe to the Stereographic projection was not taken, but instead an actual globe with the world on it with that transformation was made. It was noted that many people found it difficult to notice there was anything unusual about that globe. This is what such a globe would look like:
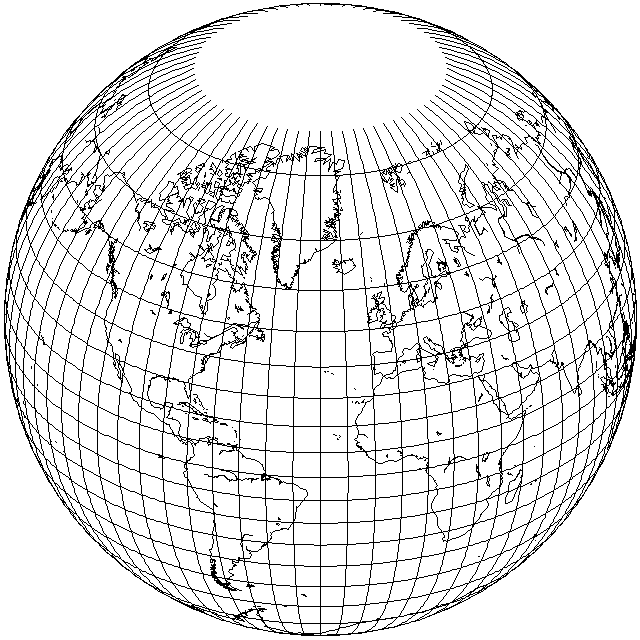
(Incidentally, this image is also a map, and its projection is known as the Gilbert two-world perspective projection.)
That many people did not notice anything wrong could be simply because conformality eliminates the most visually obvious type of error, or perhaps because of the baneful influence of the Mercator projection, which has led many to suppose that areas near the poles are larger than their actual size.
In an azimuthal projection, errors increase equally in every direction from the center of the projection. With a cylindrical projection, or a conic projection, having one standard parallel, along the standard parallel, however far it is prolonged, there is no error, but errors increase in the direction perpendicular to the standard parallel, and they do so more quickly than in an azimuthal projection.
An azimuthal projection, therefore, is well suited to a map of a country such as France, which extends about as far North and South as it does East and West. A suitable oblique cylindrical projection would be well suited to a map of Chile, or even Argentina, since these countries extend many times as far in one direction as they do in the direction perpendicular to that.
Although the Lagrange Conformal projection was devised for a world map, it may be noted that in it, errors increase, when moving north or south of the center of the map, less rapidly than in the Mercator, because some error is also admitted when going east and west, and, in addition, because the north and south error is greater than that of the Stereographic, the errors going east and west increase less rapidly than in that projection.
The 48 contiguous states of the United States of America occupy an area that is about twice as wide from east to west as it is high from north to south. A shape like this for a country or other area of interest would seem to be a sufficiently common occurrence as to be of interest.
Thus, the map below
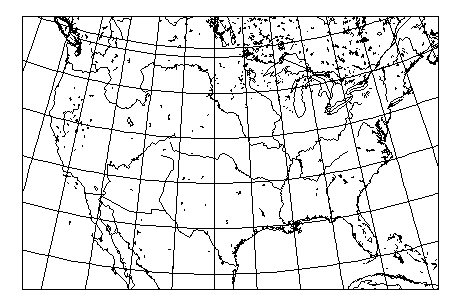
is a map of the "lower 48" as drawn in the central part of an oblique Lagrange Conformal projection centered on 40 degrees North latitude and 100 degrees West longitude.
One could, of course, do even better than this: since the mean of two conformal projections is conformal, one could search for a mathematically optimum combination of, say, a Stereographic and a Lambert Conformal Conic. (Then there is, of course, the GS50 projection, where an optimum polynomial function was searched for by computer that minimized error for all 50 states, including Alaska and Hawaii, so one can be even more ambitious than that.)
In the case of an equal-area projection, no mathematical scheme of equal directness immediately suggests itself, but again, one could use the central part of an Aitoff-Hammer projection for an equal-area map of either the continental United States (exclusive of Alaska, which, unlike Hawaii, is also on the North American continent) or any other country somewhat, but not extremely, longer in one direction than another.