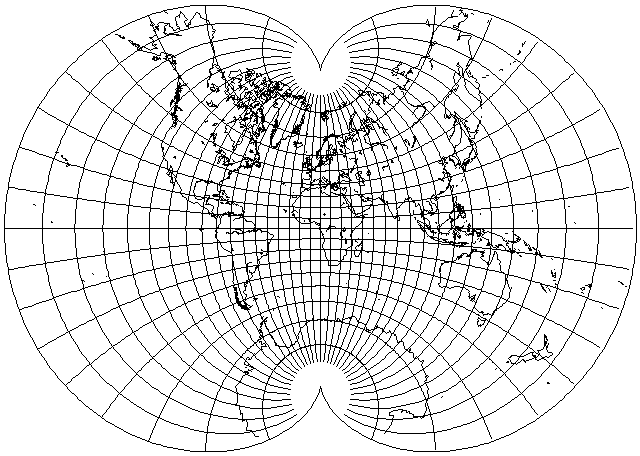
This projection is not one that you are likely to see often.

But it is a very nice projection. It is conformal, but unlike the Stereographic projection or Mercator's projection, it is possible to fit all the world in it, without any parts going to infinity.
Lagrange's projection, on the previous page, does do that, but the poles, although present, are the two points at which the projection ceases to be conformal. This projection does not even have that problem, since it has two cusps where the poles are, so that the meridians can radiate out from the poles accurately in all directions over the full 360 degrees.
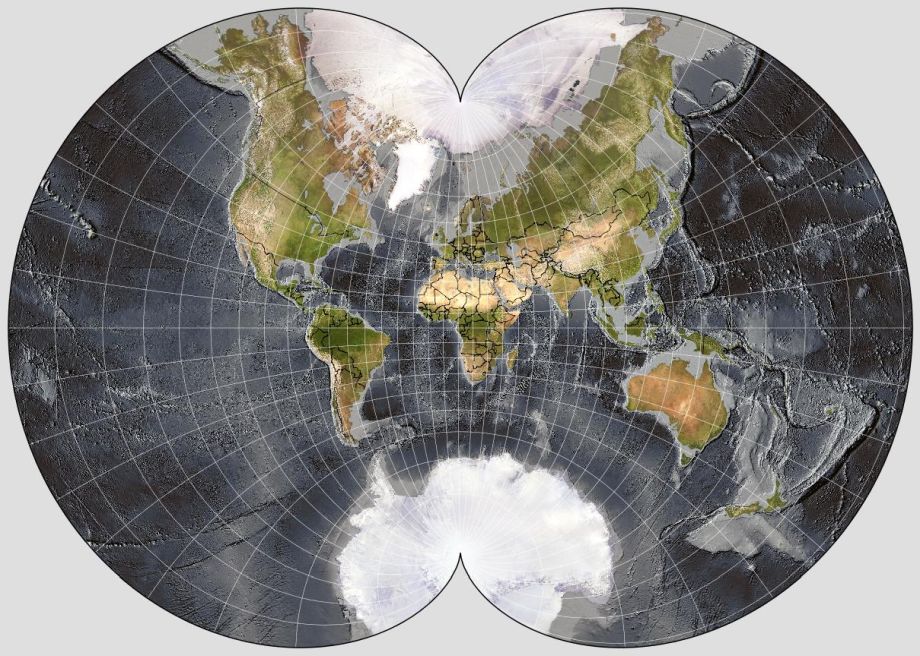
This pictorial version of the August Conformal Projection of the World on a Two-Cusped Epicycloid, created with G.Projector, and using a dataset from NOAA that provides shaded relief for bathymetry as well as topography, as it includes national borders, shows why this projection can't really be used for an ordinary map of the world for mainstream purposes: the exaggeration of scale is such at the edges that the areas in the center of the map must be at quite a small scale relative to the size of the map, compared to almost any other projection.
On the left is the version I drew with my own map drawing program, and on the right is a version I was able to create using G_Projector, using another version of Etopo as the source.
I have finally found another equirectangular basemap that I could use which had a somewhat more dramatic presentation of ocean relief, and so here is another one produced with G_Projector:
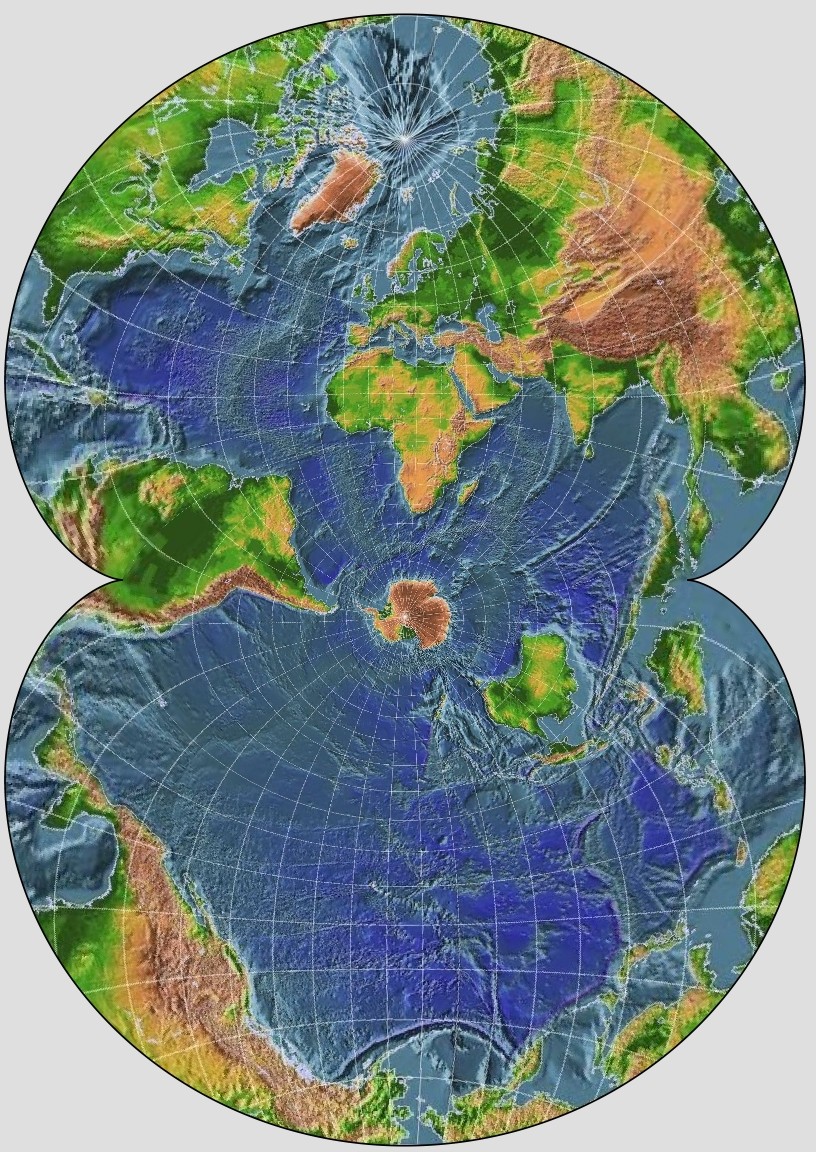
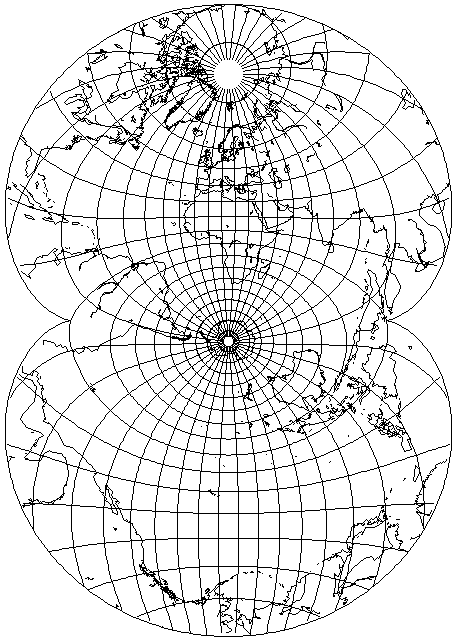
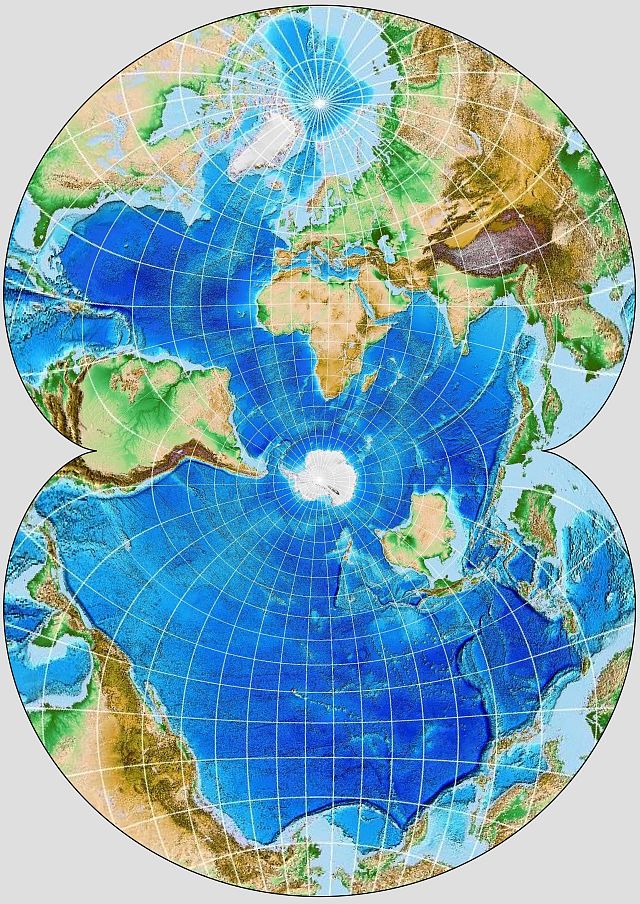
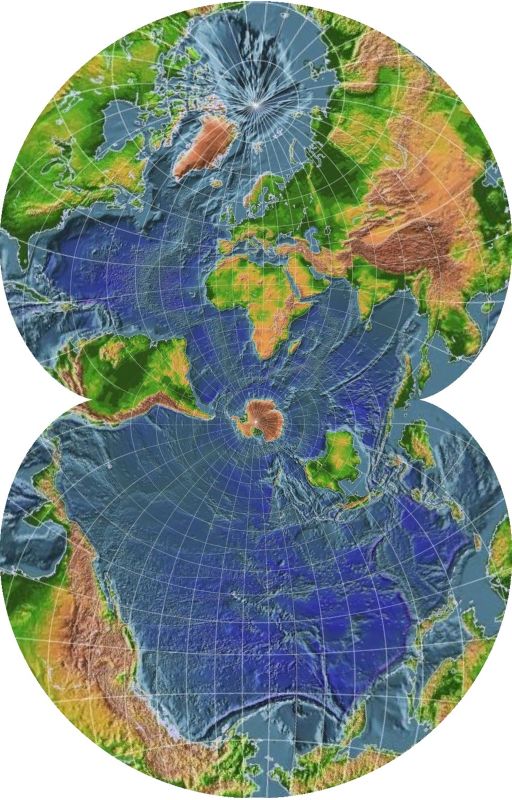
But because it has the property of being a conformal projection of the entire globe that is both conformal everywhere and which takes up a finite amount of space, this projection was used as the basis for a famous map of ocean currents that you may have run across, and which is perhaps the only place many people have seen this projection. The illustration above shows, at least approximately, the particular transverse form of this projection used for that map. It first appeared in a paper, "Maps of the Whole World Ocean", by Athelstan Spilhaus, in the July, 1942 issue of the Geographical Review.
(Dr. Spilhaus continued working on mapping the oceans of the world continuously on a single map after that; another projection he designed for the purpose of showing the world ocean in 1979 or 1980 was displayed on a web page which, unfortunately, is no longer available. He passed away at age 86 on March 29, 1998.)
His 1942 map was a line drawing, filled with arrows showing the directions of the ocean currents. I've tried to make maps in the same aspect and projection using sources showing the relief of the ocean floor as vividly as possible.
Because I was thinking of an even more famous map concerned with all the oceans of the world. One that was on another conformal projection, but just the plain old Mercator, and which came out in 1977.
Of course, I am referring to the famous map of the ocean floor which was due to the work of Bruce Heezen and Marie Tharp, and which was painted by Heinrich Berann.
Several years previously, there were published maps that Marie Tharp had drawn of the floor of the Atlantic ocean; the first, of the North Atlantic, was published in 1957 in the Bell System Technical Journal, and the second, of the South Atlantic, was published in a monograph in the Special Paper series of the Geological Society of America.
The Mid-Atlantic Ridge was first clearly and conspicuously visible in these maps; as it was strongly suggestive of the truth of Wegener's theory of continental drift, as well as the theory of plate tectonics as the mechanism for that drift, and this was not generally accepted at that time, while Marie Tharp was strongly in favor of letting the facts speak for themselves, she met with resistance from her collaborators, both Heezen and Maurice C. Ewing. After 1957, however, several geologists, particularly Henry Hammond Hess, published papers with research that made continental drift more plausible by laying the foundations of plate tectonics, and so continental drift soon became at least a respectable idea, and then eventually became the new orthodoxy.
Heinrich Berann worked for the National Geographic Magazine, and also painted the maps of the ocean floor which were included in several issues of that magazine.
I had, indeed, seen this version of August's Conformal before first seeing it in its conventional orientation in Elements of Map Projection with Applications to Map and Chart Construction by Charles H. Deetz and Oscar S. Adams. Here is the map I saw there:
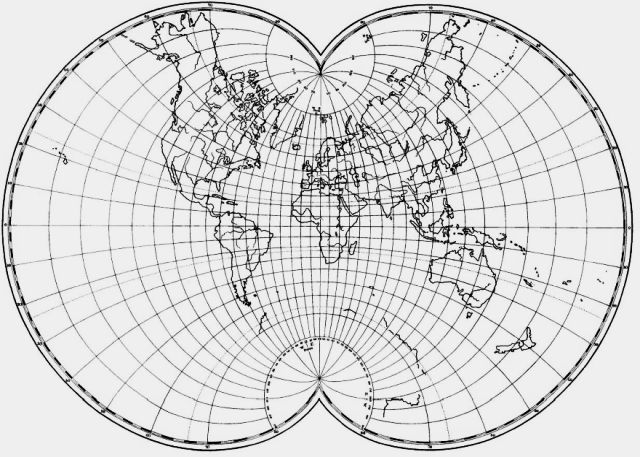
At this scale, one unusual thing about this map is not visible. The map is drawn on the Paris meridian instead of the Greenwich meridian, with longitudes west and east of Paris marked on the top, and west and east of Ferro, with the Ferro meridian as 20 degrees East by the Paris meridian, on the bottom.
While an international agreement to accept the Greenwich meridian was reached in 1884, France did not adopt it until 1914, although earlier, in 1911, they switched to setting their clocks according to the Greenwich-based Standard Time system.
The Paris meridian is about 2° 20' East longitude. Another notable meridian used for some purposes is the Washington meridian, particularly the one based on the Old Naval Observatory; this was at about 77° 2' West longitude, and the borders of some American states are based on this meridian. The Azores yield a meridian at 25° 40' West longitude (this specific value is from a relatively late proposal for the use of this as a standard meridian), as this is to the West of the entire Old World, it avoids the use of negative numbers, and thus this was the earliest standard meridian, corresponding approximately to what is given in Ptolemy's Geographia.
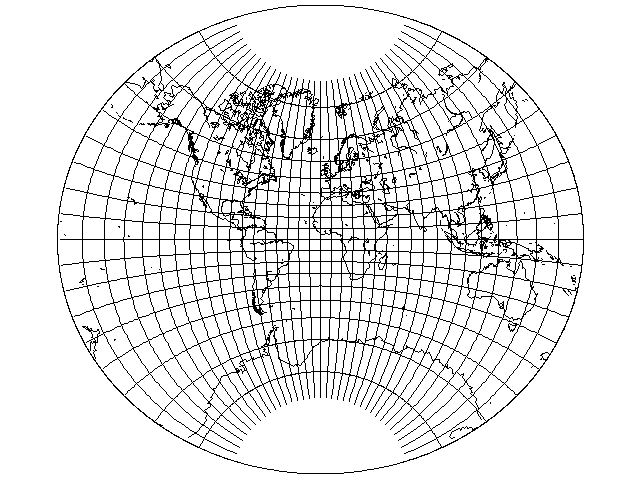
Of course, one can place the world on this projection in many orientations.
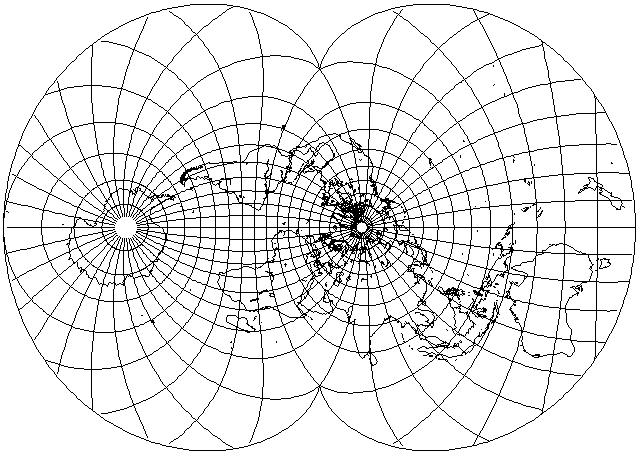
This map is one attempt to place the world in a useful orientation on this projection. Note, though, that while Australia is placed in a part of the map where it is very much enlarged, its general shape is less distorted than that of parts of Asia, where the scale is smaller, but changes more rapidly.
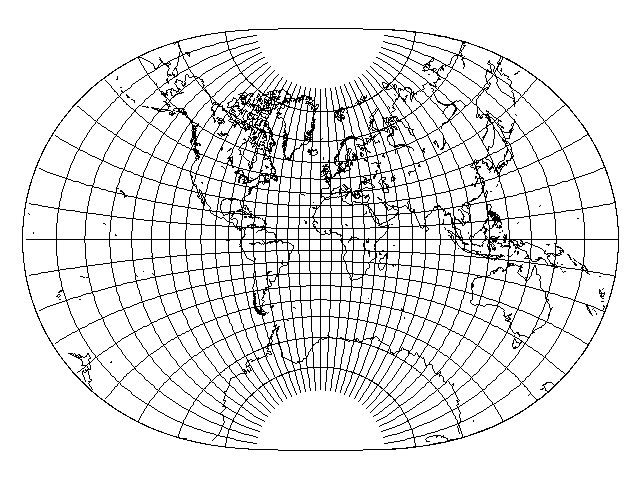
Here is another version of this projection, this time in an oblique case rather than a transverse case:
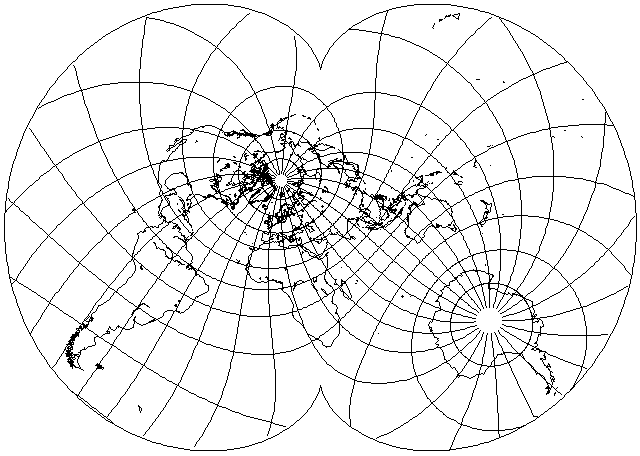
this is in fact the same orientation that I used for maps in the Mollweide projection and the Hammer-Aitoff projection.
How is this projection made? The first step is to take the world, and project it using Lagrange's projection, so that the world is conformally mapped to a circle.
Then, the circle is conformally mapped to the inside of the epicycloid that forms the boundary of the map using complex numbers. Functions over the complex numbers are an inexhaustible source of conformal mappings, since functions are extended to complex numbers in the fashion that permits them to be differentiable over the complex plane, and the condition for differentiability and for forming a conformal mapping are one and the same. Of course, one can form many useless conformal mappings into weird shapes that way, but many very useful conformal maps have been found using complex numbers.
The Lagrange projection of the globe is placed on the complex plane so that the north pole is at z=1, and the south pole is at z=-1. Then, the function 3z-z^3, which has inflection points at z=-1 and z=1 along the real line (places where it changes from increasing to decreasing or back again, like the sine function at 90 degrees and 270 degrees) is used to map the Lagrange projection to August's projection. It is because of the inflection points that one gets the cusps in the bounding curve; one could use the sine function instead to make a projection that looked somewhat like August's projection.
This can be illustrated by the following image, in which a map of the world on Lagrange's conformal projection is superimposed on a gradient diagram of the function 3z-z^3. The three zeroes of this cubic polynomial are clearly visible on the real line as areas bounded by approximate circles, and the fact that angles are doubled at the inflection points can also be seen.
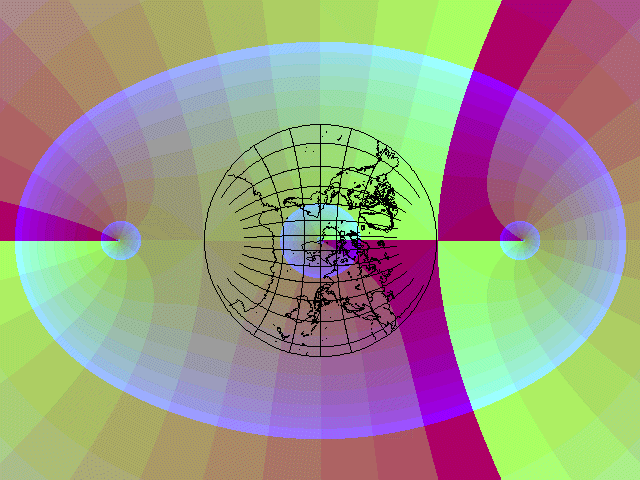
The conformal transformation involved can be seen in action by means of the following diagram, containing a gradient diagram of the identity function (with the axes on a larger scale) on which a map in August's conformal projection is superimposed:
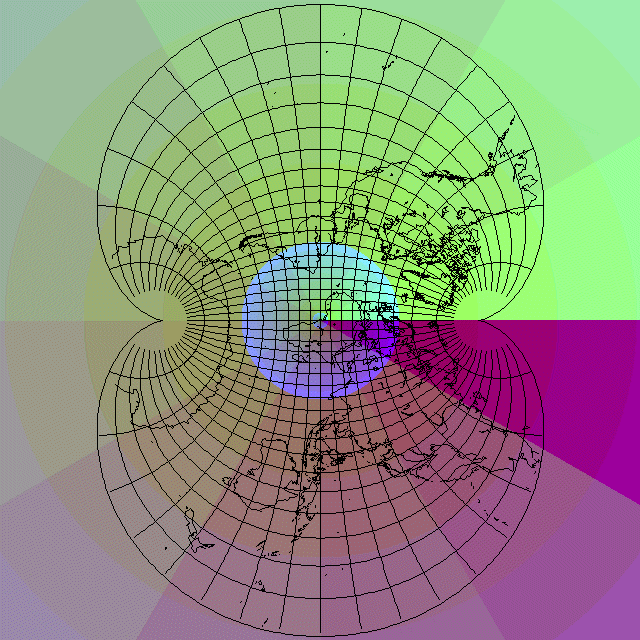
corresponding areas on the maps in the two images are the same color within the gradient diagram. The North Pole of the Lagrange projection is on the point 1+0i in the first diagram, where 3z-z^3 evaluates to 2; in the second diagram, the North Pole of August's Conformal Projection is on the point 2+0i, where the identity function, z itself, also evaluates to 2, and hence both points are on the corner between the same four colors (which are in two groups of two colors which do not contrast very well; that there are four colors and not two is perhaps a bit easier to see around the South Pole) in the gradient diagram, which bound the areas with amplitude from 1 to 2 and 2 to 3, and phase from 330° to 360° and from 0° to 30°.
The behavior of the inflection points for complex arguments is also important, because the cusps could easily wrap around for other functions. Note, of course, that for the sine function, the circle with radius pi/2 is used instead of the unit circle.
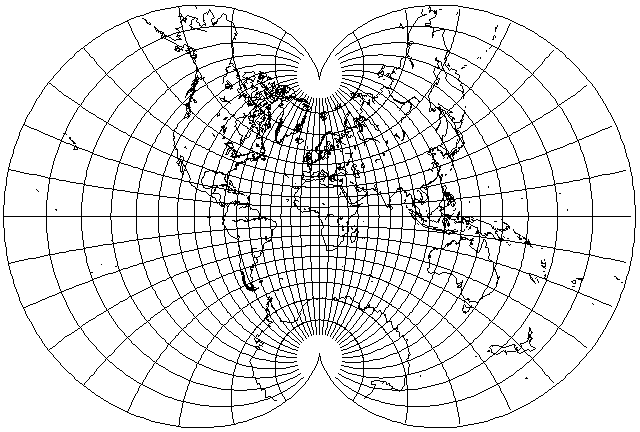
And the above is the projection I first produced on my Commodore 64 computer before I was able to determine the actual formula for August's Conformal projection. This projection has a close resemblance to the Eisenlohr, but it is not the same as that projection.
This projection appears to have greater size distortion than August's conformal, and the Eisenlohr would appear to be even slightly worse, but in fact the Eisenlohr, because it has a uniform scale everywhere along its boundary, has the minimal overall distortion of size.
Here is the actual Eisenlohr projection itself:
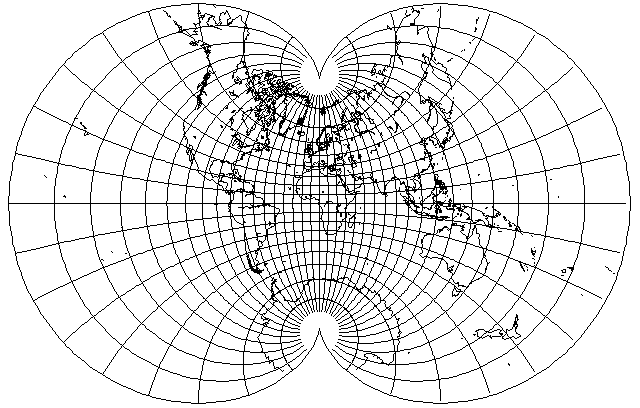
Why are appearances decieving? Although August's conformal projection has greater size distortion near the poles, it has less distortion for areas on the Equator far from the central meridian. For world maps in conventional aspect, this will appear to be more important, but for applications where every part of the globe is equally important, the Eisenlohr would be advantageous, despite being somewhat more complicated to calculate.
As I had some difficulty in implementing the Eisenlohr, despite having located equations for it, and as information about the projection is difficult to locate on-line, it may be helpful to provide the equations for this projection, essentially as they appeared in "An Album of Map Projections" by Snyder and Voxland (USGS Professional Paper 1453), but also confirmed by my having finally successfully coded the projection:
long
S1 = sin ( ---- )
2
long
C1 = cos ( ---- )
2
lat
sin ( --- )
2
T = ----------------------------------------------
______________
lat / cos( lat )
cos ( --- ) + 2 * C1 * / ------------
2 \/ 2
_______________
/ 2
C = / ------------
/ 2
\/ ( 1 + T )
__________________________________________________
/ _______________
/ lat / cos( lat )
/ cos ( --- ) + ( C1 + S1 ) * / ------------
/ 2 \/ 2
V = / -------------------------------------------------
/ _______________
/ lat / cos( lat )
/ cos ( --- ) + ( C1 - S1 ) * / ------------
\/ 2 \/ 2
1
x = C * ( V - --- ) - 2 ln( V )
V
1
y = C * T * ( V + --- ) - 2 atan( T )
V
X and Y are scaled up by a factor of 3 plus the square root of 8 in the equations as given, omitted above for simplicity; but this causes X to range between plus and minus 2 times pi; so, for my program, where I scale everything to being from -180 to +180, I multiply by 90/pi, and use 166.9721 as my scale factor.
Incidentally, the two terms in the expansions of x and y are each conformal projections in themselves; x = ln(V), y = atan(T) produces a conformal projection in a shape resembling an ellipse with a limited elongation. (However, the shape is unlikely to actually be an ellipse; elliptic integrals, as used for Guyou's projection, to be seen next, are required for that.)
Here is the part that looks like an ellipse; this part is called the beta component of the Eisenlohr:
And here is the part, called the alpha component, from which it is subtracted; as it has flattened tops at the poles, the difference has the required cusps:
The reason the Eisenlohr projection is optimal is because the scale is uniform on its boundary; a conformal projection from one region to another is optimal when the condition of uniform boundary scale is met. But there is no reason why the world has to be conformally projected on any particular shape. Thus, shortening the extent of the link between the two hemispheres might improve the projection, since two Stereographic hemispheres have a lower distortion than a conformal map of the whole world.
The Eisenlohr projection was devised by Friedrich Eisenlohr in 1870. A mathematician by that name lived from 1831 to 1904, and the German-language page about him does include the 1870 publication in which this projection was first described, Über Flächtenabbildung among his publications, so, indeed, he is its inventor. There was also an architect by that name, who lived from 1805 to 1854, and thus who could not have been responsible for the map projection, but who is instead famous for designing the modern form of the cuckoo clock.
Friedrich August invented his projection in 1874. As noted, while theoretically it is inferior to the Eisenlohr, which has the absolute minimum of total overall size distortion possible for a projection of the sphere with that particular epicycloid as, its boundary, it appears to have less distortion because for a world map in a conventional aspect, there is less distortion in the areas that are considered to be of importance.
However, Friedrich August was not content with making that distinction, and in the initial paper describing his projection, he claimed his projection to be simply superior to the Eisenlohr, resulting in a paper by Eisenlohr in reply.
Given that August's conformal projection only looks better than the Eisenlohr for a world map in the conventional aspect, but the Eisenlohr is the optimal projection for the case where every part of the globe is equally important, it would have been the better choice for Athelstan Spilhaus' map of the world ocean, or at least so I would think.
While I could have drawn an outline map in the Eisenlohr projection in that aspect with my own map drawing program, I didn't think that would be all that illuminating. But G.Projector does not support the Eisenlohr projection; which isn't surprising, as it is difficult to invert, being the sum of two component projections.
However, imagine my joy at discovering the latest updated version of Justin Kunimune's Map Designer program does allow raster maps in the Eisenlohr projection to be plotted! So feast your eyes...
Another case where all parts of the map are equally important, so that the Eisenlohr would be preferred to the August conformal, is for maps of other celestial bodies, such as the Moon or Mars. So here is a map of the Moon on the Eisenlohr projection:
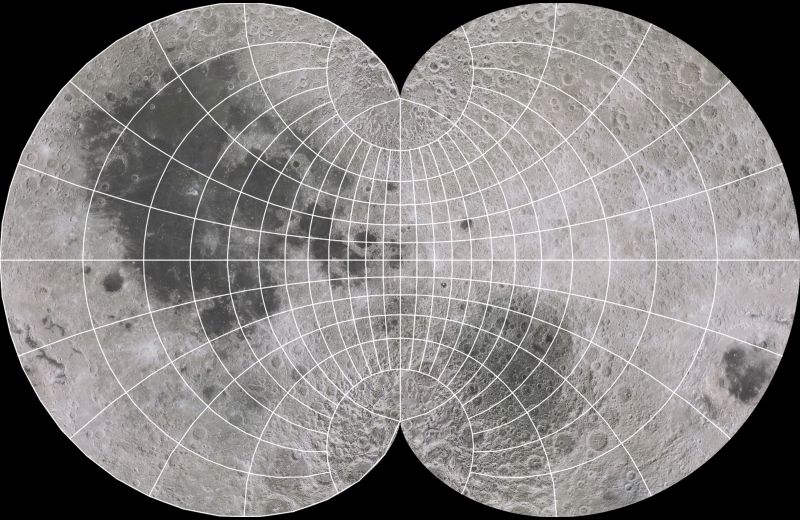
Of course, though, this is not really a particularly good example. While one can achieve a small improvement by going from August's conformal projection to the more mathematically complex Eisenlohr, one can get an even bigger reduction of the distortion of sizes in the map by going to the mathematically simpler Stereographic in the form of two hemispheres:
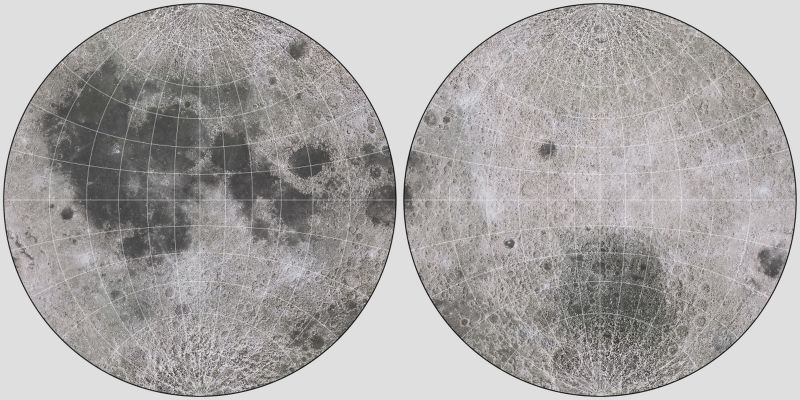
and, as well, since we see the Moon as round in the night sky, such a map accords well with our conventional thinking about this celestial body.
One might map a polar Stereographic projection onto one with a smaller scale, such that its equator coincides with 45 degrees north latitude, and then place the pole of the result in the center of a map using the cosine-based projection above to attempt to move towards the lower distortion of two Stereographic hemispheres by reducing the connection between the two halves of the projection. The following
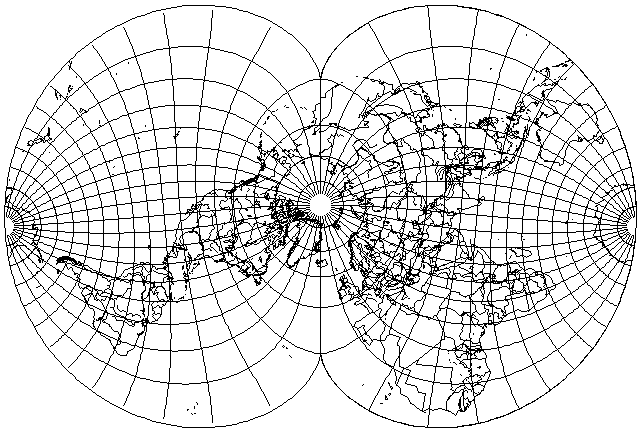
is an oblique case of this projection, tilted five degrees backwards along the prime meridian. Instead of the center being at a smaller scale, it is now at a larger scale than the rest of the map; a further transformation to improve the map by making the scale more closely constant should be possible, and this would provide an interesting conformal projection.
If we use August's projection, and reduce the amount of central expansion by stretching 130 degrees instead of 90 degrees to fill the 180 degree-long prime meridian, we obtain:
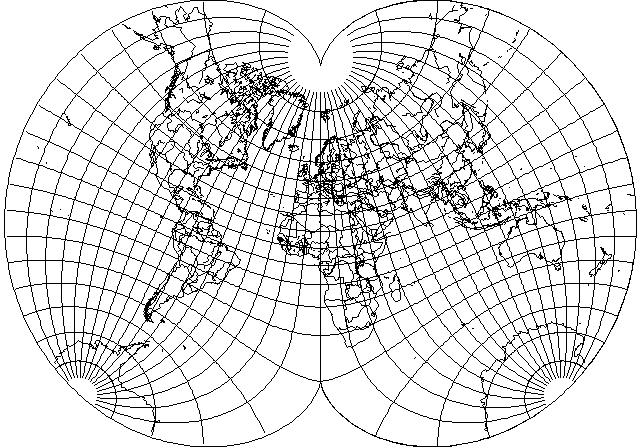
which, although it is still not perfect, is very nice for a conformal projection.
This projection suggests, however, that if one wishes to be completely unabashed about showing Europe on a larger scale than the rest of the map, one could construct a map like the following:
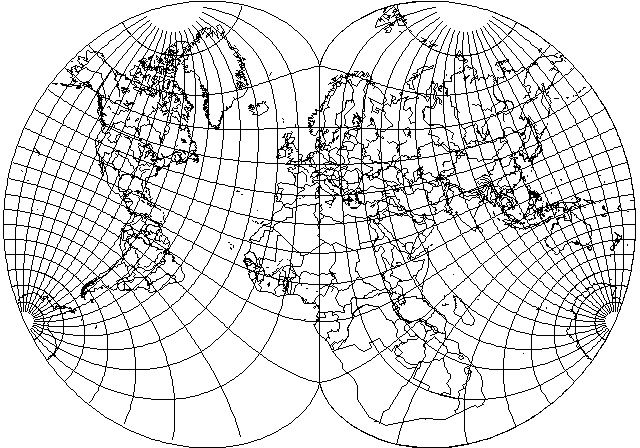
but Europe is not enlarged by all that much even on this map.
To compare stretched versions of August's conformal and the Eisenlohr directly, here is how they compare when used to produce what might be considered a compromise between a Mercator projection and two Stereographic hemispheres side by side:
Here is August's conformal, with 140 degrees stretched to fill the central meridian:
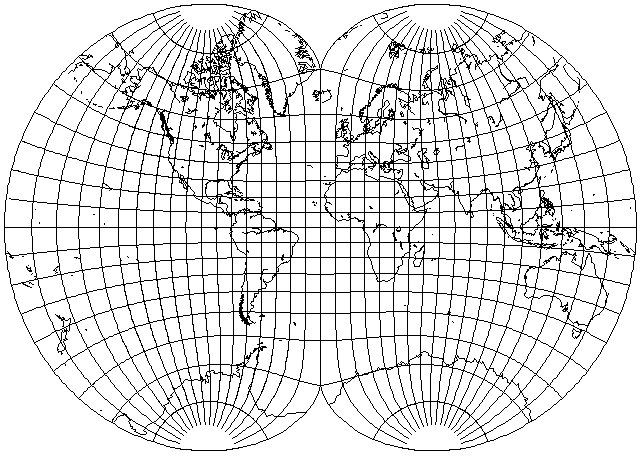
And here is the Eisenlohr, with only 120 degrees stretched to fill the central meridian:
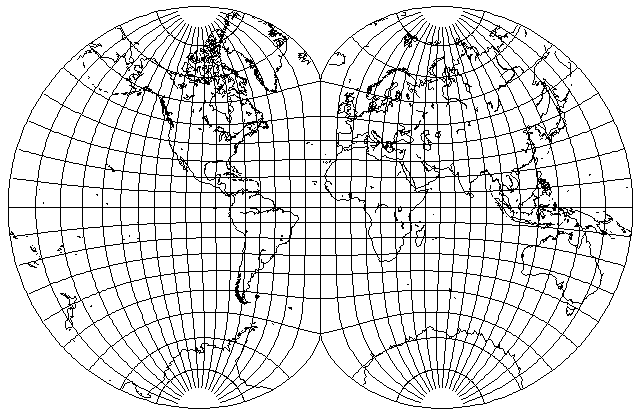
In both cases, they resemble the Mercator sufficiently as not to seem to be any great improvement on it.
Also, the availability of a little extra space on the transverse aspect of August's projection shown above suggests the benefit of using only a very modest amount of central expansion (expanding 150 degrees to cover the central meridian) as shown here:
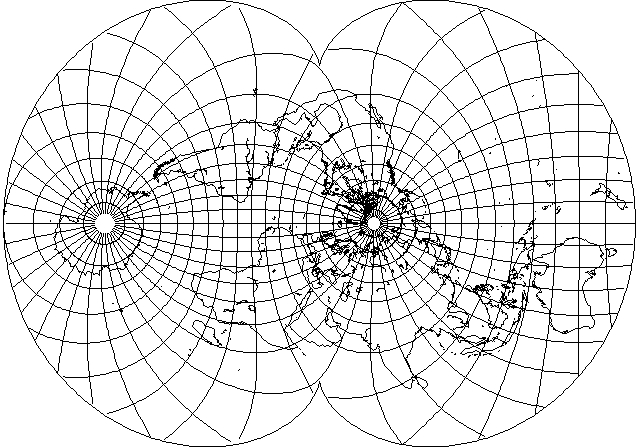
Here's an example of using another transformation, the compression used to produce the Lagrange conformal or the conformal conic, to attempt to reduce distortion, but it doesn't seem to have been successful:
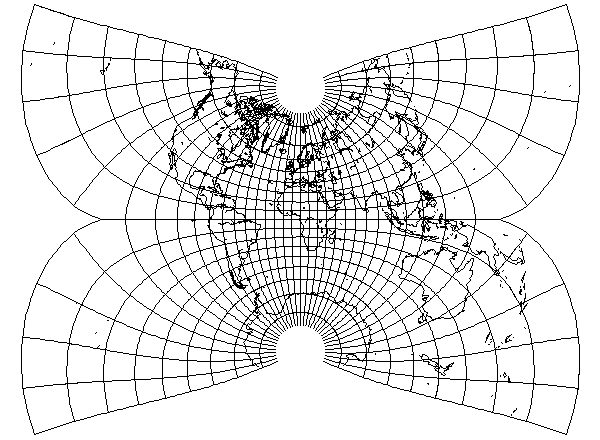
As an example of the possible pitfalls one might encounter when working with complex numbers,
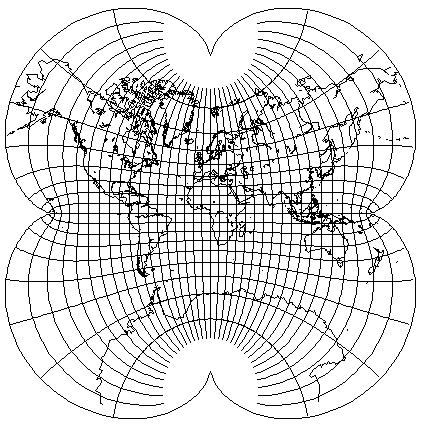
basing a projection on the equation 5z-z^5 instead of on 3z-z^3 does produce cusps of the right shape at the poles, but unfortunately it also produces two extra cusps on the Equator.
Since complex-valued differentiable functions produce conformal mappings, their sums remain such functions. If one takes two August's projections rotated by 90 degrees - with the world within them rotated as well - it should be possible to position the cusps so as to obtain a conformal projection with fourfold symmetry:
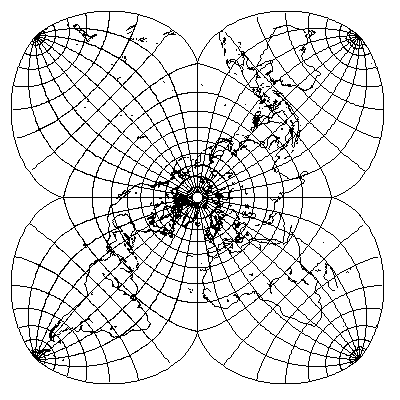
however, it is surprisingly not conformal at the South Pole, despite the fact that both component projections have sharp corners at that point.
Doing the same with two Lagrange's projections obtains the following:
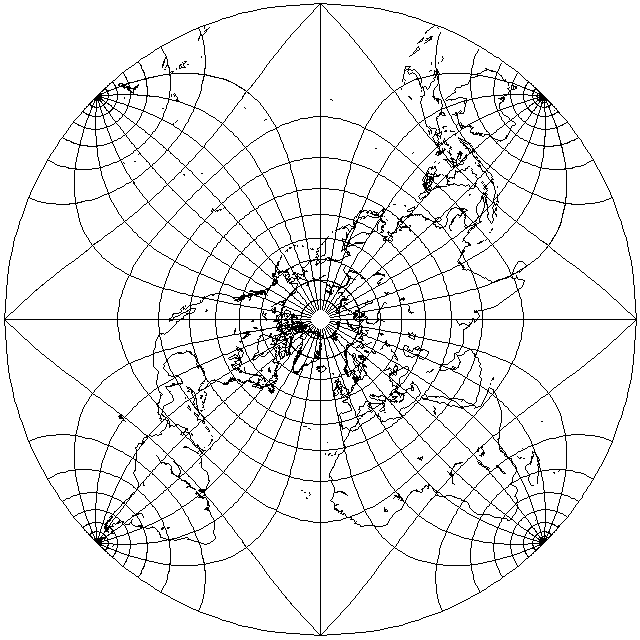
which is interesting because the Northern hemisphere is given sharp corners; this allows one to avoid use of elliptic integrals to obtain the opposite distortion of the one provided by 5z-z^5, halving angles at four points instead of doubling them.
Also, note that the scale distortion is surprisingly moderate over most of the map for a conformal projection. However, Antarctica is shrunk almost to invisibility on this map. The fact that the extremes of scale distortion are manifest as shrinkage instead of enlargement also makes this an unusual conformal projection.
Attempting to sum together two August's projections, but with the world tilted forwards by 90 degrees in one, to get a projection with the two halves joined along a line 90 degrees in length instead of 180 degrees in length, to get less distortion by being closer to the case of two independent stereographic hemispheres, instead of doing so by the technique shown above of mapping Stereographic projections of different sizes on each other, obtains the following:
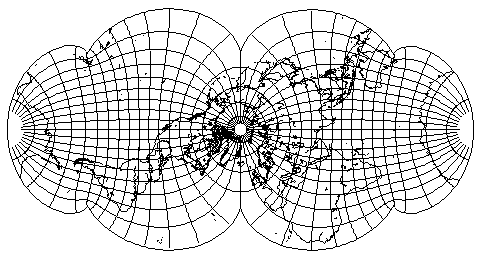
which is marred by the emergence of some unexpected cusps.
Incidentally, since most normal mathematical functions, when applied to complex numbers, produce conformal mappings, a projection called the GS50 projection was devised which started from a Stereographic projection, and then transformed it using a high-order polynomial the terms of which were determined by a computer optimization process, to produce a projection which had very low scale error for the continental United States, and for Alaska, and for Hawaii, while having higher error elsewhere, on one single continuous map.
Why should I torment your curiosity, only mentioning it here? Ah, but it's not as if anyone who was curious, and who has access to the Internet (how else could you be reading my web site, after all?) could not just easily satisfy that curiosity with Google. Still:
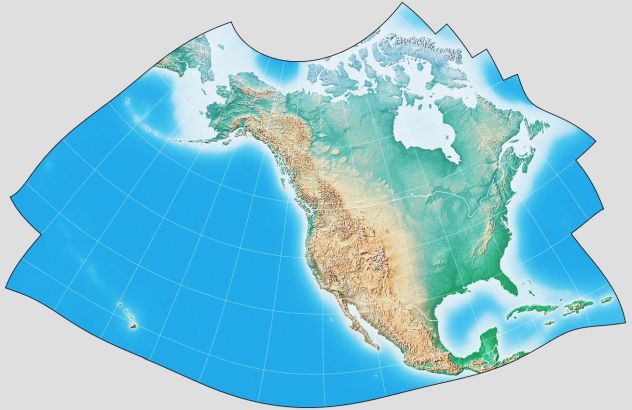
since G.Projector will draw a map on that projection for me, why shouldn't I make one and share it with you? And then, to see what is going on here,
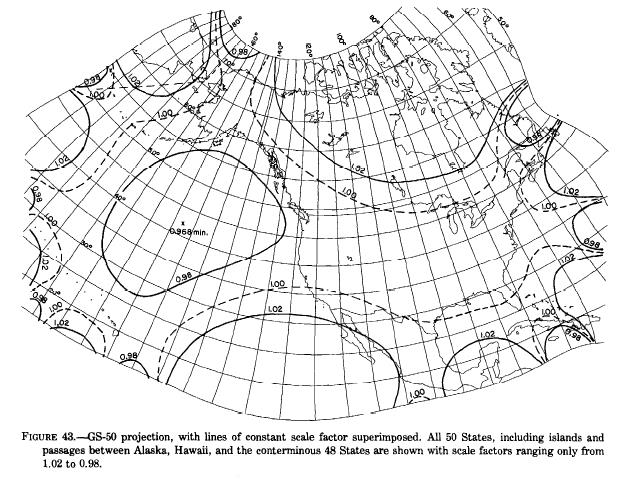
from Map Projections: A Working Manual, U.S. Geological Survey Professional Paper 1395 - by John P. Snyder, who developed this projection, as it happens - a diagram showing the distribution of errors of scale (there is no angular distortion, it is conformal) on the projection.
This projection is an amazing tour de force to illustrate what the mathematics of conformal projections is capable of. Why has it not also achieved wide popular adoption in the United States?
For one thing, if the purpose of a map of the United States is to show what is present, or what is happening, within the United States, showing all the space between the lower 48 states and Hawaii and Alaska in the Pacific Ocean is an inefficient use of space, which is often at a premium.
In order to be optimal for those parts of the area which it depicts that are part of the United States of America, it allows the scale to behave in a less-than-uniform manner everywhere else.
To depict the relationship between Alaska, Hawaii, and the "lower 48" states of the United States of America, if that is the goal of a map, nothing beats an Orthographic:
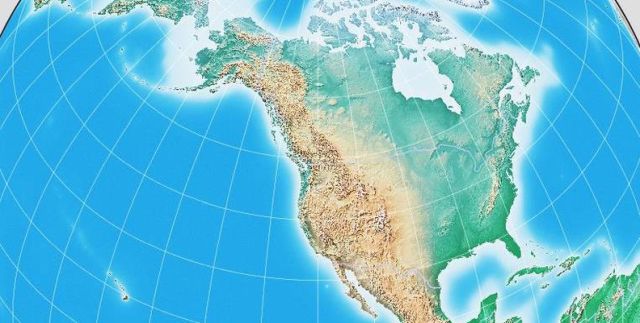
For almost any other purpose, depicting Alaska and Hawaii with inset maps and more ordinary projections is virtually mandatory.
As a tour de force to demonstrate the mathematics of conformal projections, it is a great accomplisment. As a projection of practical utility, I am afraid that the neglect in which it languishes is fully justified. But I don't see that as a reason for sadness. Instead, it can be an opportunity to gain insight into what is actually demanded of map projections.