The graticule of this projection just might look familiar

if you've ever looked through Jahnke, Emde, and Lösch, and looked at the gradient diagram for the Jacobian amplitude in it, which appears somewhat similar to the following:
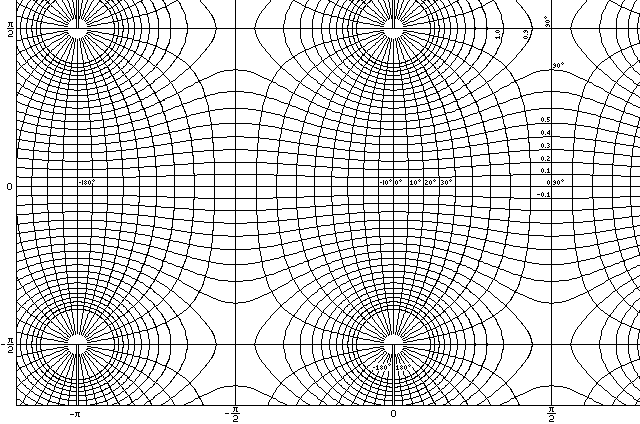
although this chart is made for k=pi/2, the complete elliptic integral, not k=0.8 as in the example there.
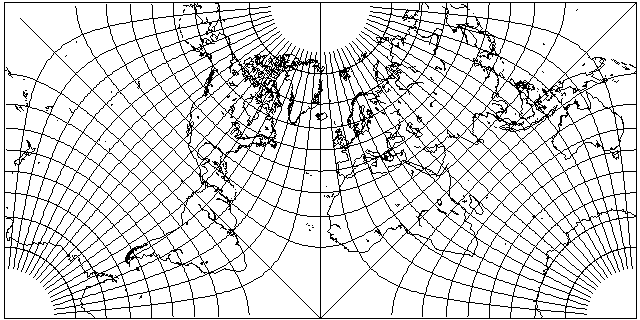
Yes, this map projection is plotted with the aid of elliptic integrals. And the main thing about it that makes it of interest, in addition to the fact that it is conformal, is the rather banal fact that the hemispheres on this projection can be made into tiles, as illustrated below:
If we tilt the world forwards by 45 degrees, we see that this projection is symmetrical, and we obtain another pleasing arrangement.
More advanced uses of elliptic integrals are also possible, allowing the world to be conformally projected to a number of useful shapes. Thus, for example, instead of using the Gnomonic projection to project the globe to the faces of a regular polyhedron, elliptic integrals can be used to make each face conformal instead.
Using the same method that Lagrange's projection used to place the world on a hemisphere, the two cases of the projection above can easily lead to conformal projections of the world on a square, both orthogonally, as shown by this map:
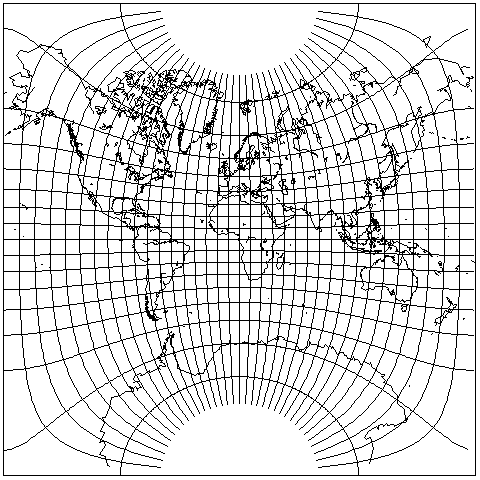
or on this prettier version, drawn by the NASA program G.Projector:
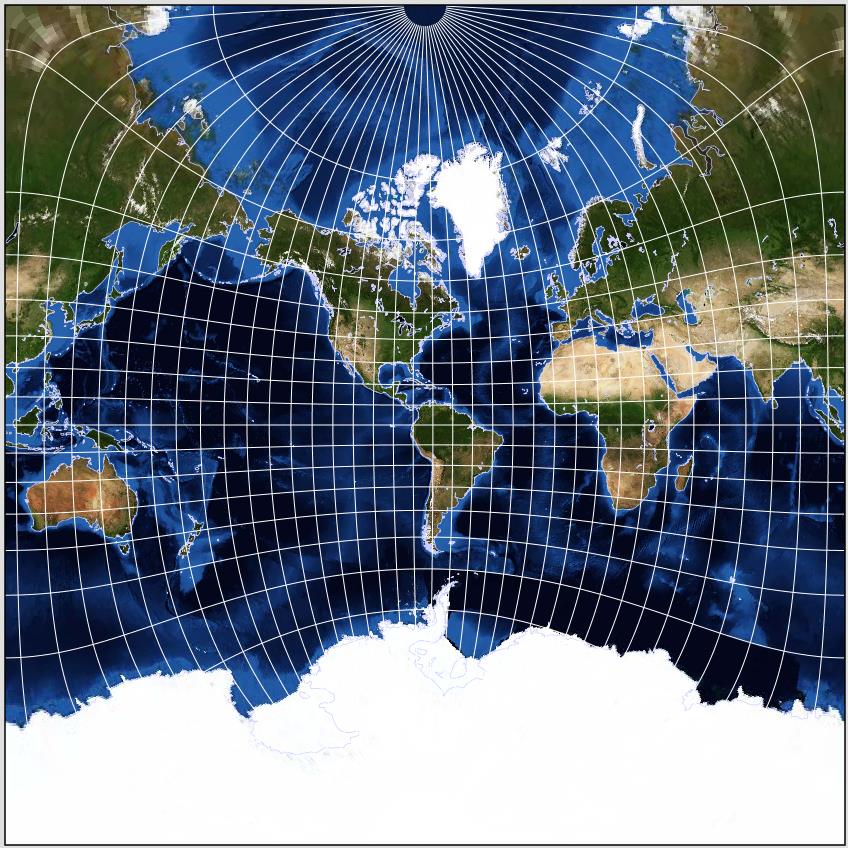
and diagonally, as this one illustrates:
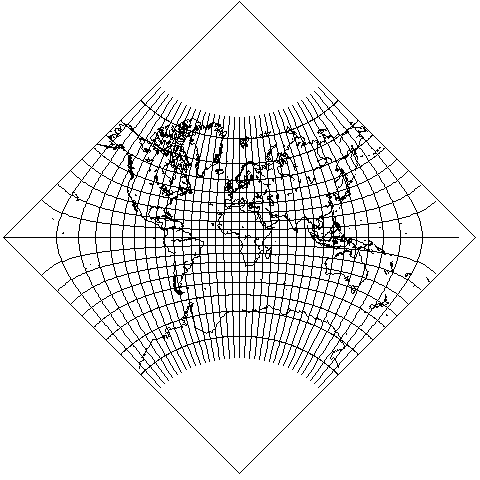
Also, by varying the parameter (or the modulus, or the modular angle) of the elliptic integral, a rectangle instead of a square can be obtained:
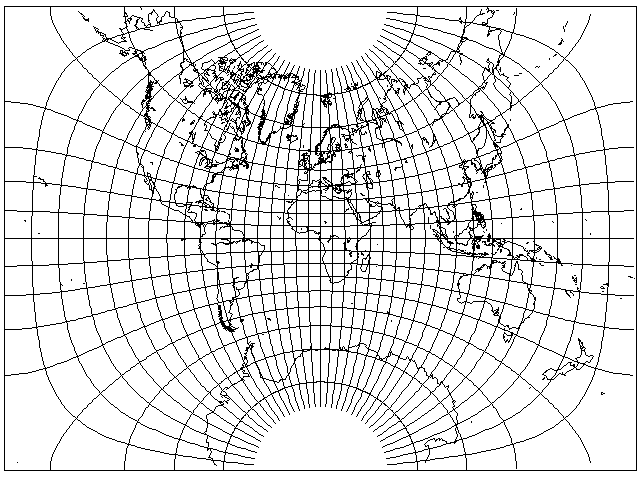
The above map was created with m=0.8 (k=0.89443, alpha=63.435 degrees) for an aspect ratio of 1.36007.
This map was created with m=.970565 (k=.9851726, alpha=80.121 degrees) for an aspect ratio of 2.000025:
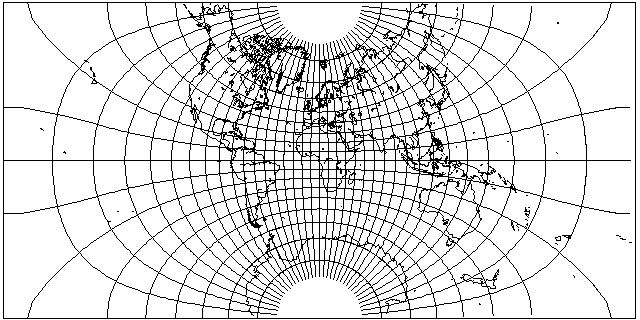
This map was created with m=.998705 (k=.9993523, alpha=87.938 degrees) for an aspect ratio of 2.9886:
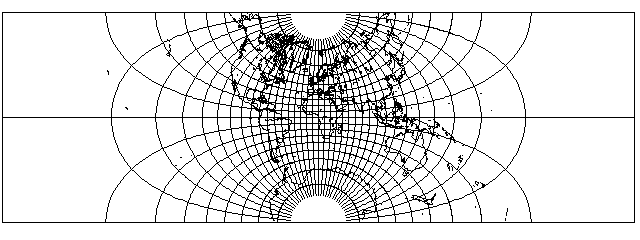
Looking at that last image suggests that the limiting case of this is the projection obtained by applying the same trick as used with the Lagrange projection to the Transverse Mercator:
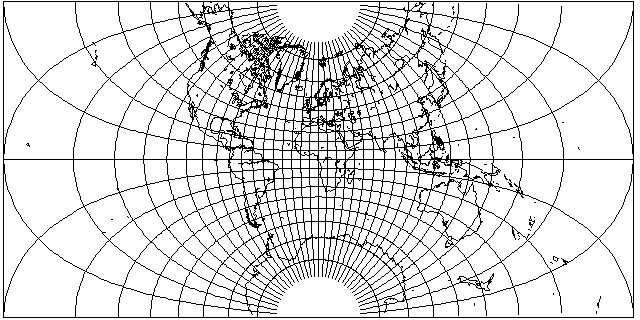
like the Mercator, this projection extends to infinity, but here at the sides.
Here is another symmetrical layout of this projection:
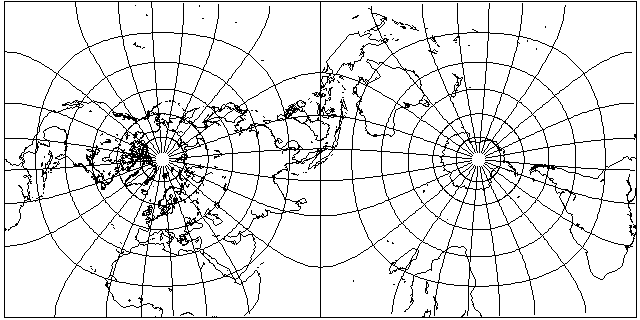
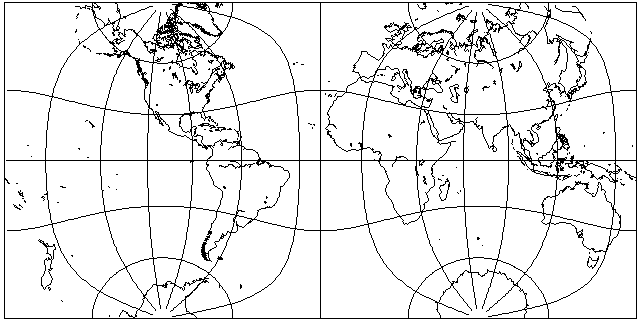
Incidentally, this layout is also possible, and is known as the Peirce Quincuncial projection:
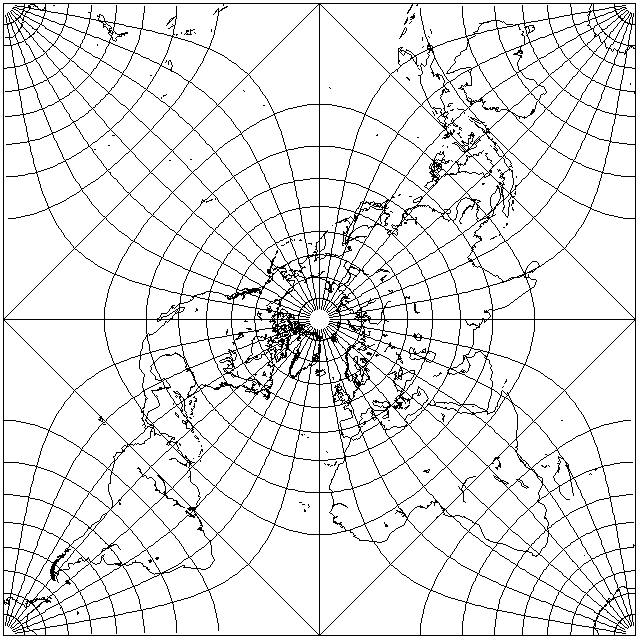
The four squares of which this projection is composed correspond to the diamond or lozenge shapes formed from a pair of equilateral triangles in projections based on the Cahill octahedral projection. Here, longitude 20 degrees West is used as the dividing line, a common one used with octahedral projections.
Here, though, is a Pierce Quincuncial projection based on 22.5 degrees West as the dividing line, the one originally used by Cahill:
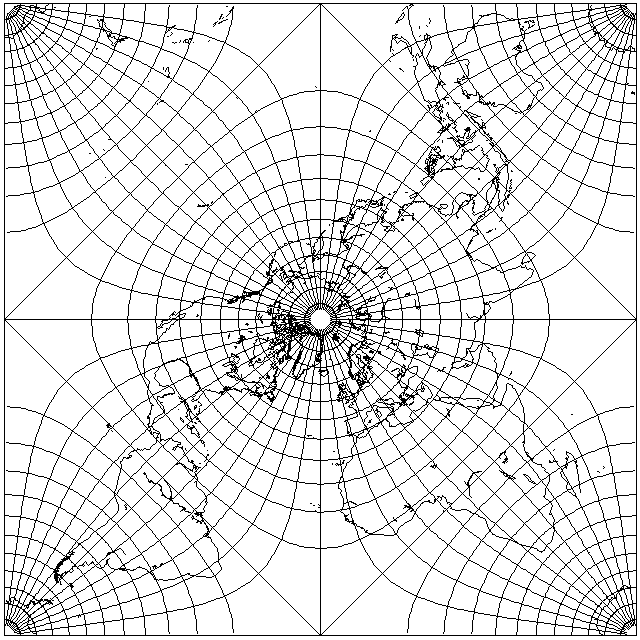
and it also shows a graticule marked at 7.5 degree intervals, so that 22.5 degrees is on a marked parallel line, as was used by Cahill in his original drawings of his projection.
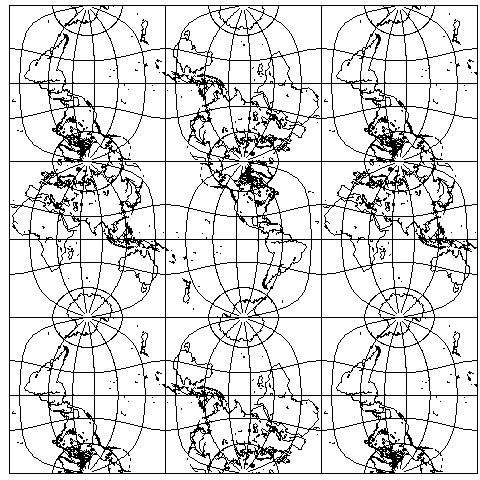
As it happens, the Pierce Quincuncial, like Gouyou's Doubly-Periodic projection, is capable of tesselating the plane in a coherent fashion:
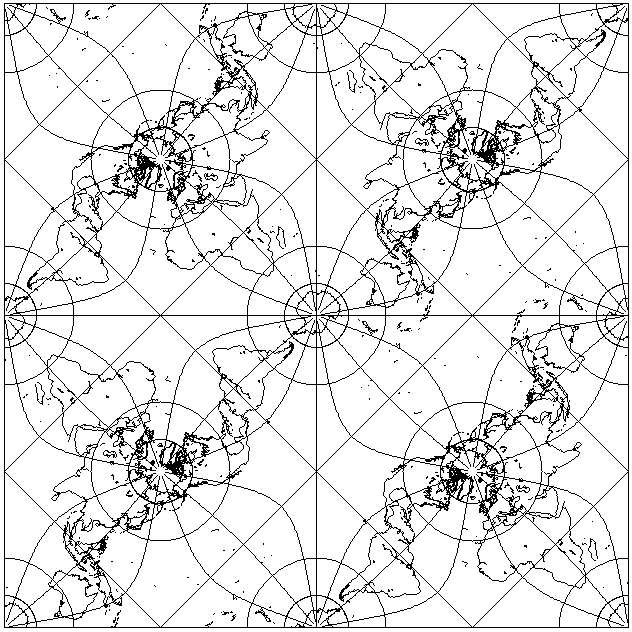
as this diagram shows.
Also, the position of the locations where the projection is not conformal just happens to match the transformation 5z - z^5 which we met on the previous page, allowing us to produce the following projection:
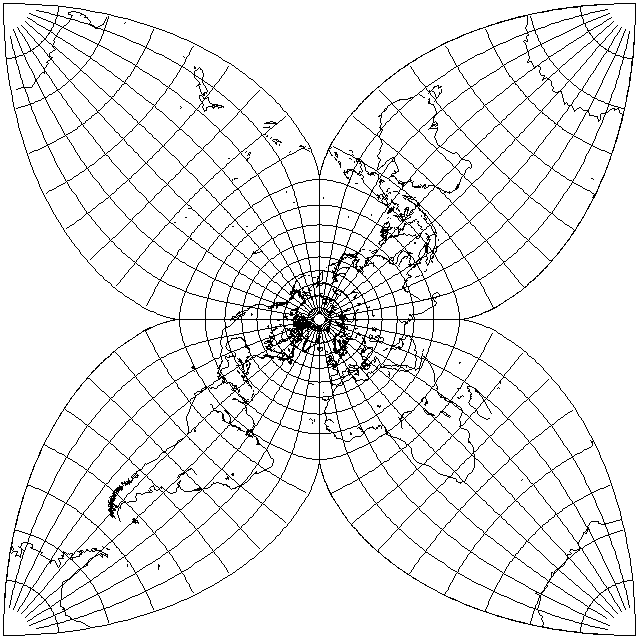
however, one would think there would be some way to do this kind of thing without resorting to elliptic integrals, and also perhaps with less scale exaggeration.