In 1925, U. S. Coast and Geodetic Survey special publication 112, "Elliptic Functions Applied to Conformal World Maps", by Oscar S. Adams was issued. In addition to recounting some previously-known maps based on conventional elliptic integrals, such as Gouyou's Doubly-Periodic and the Peirce Quincuncial, and, as mentioned on the previous page, Adams' conformal projection of the sphere on an ellipse, it also described the Dixon elliptic functions, and showed several maps in projections based on those functions.
While the best-known elliptic integrals are suitable for conformally mapping the globe into a square or a rectangle, Dixon elliptic functions have a rhombic recurrence region with 60 and 120 degree angles, and thus they can be used to map parts of the world into equilateral triangles.
Apparently B. J. S. Cahill, developer of an attractive conventional world map projection (not shown on these pages, because it has abrupt changes of direction like the Goode Homolosine within its faces) dividing the world into octahedral octants, caught wind of this publication, and persuaded Oscar S. Adams to work out a conformal map of the world with an octahedral division in 1929.
While that projection was absent from those in the 1925 work, it was closely related to them, basically differing by the Lagrange projection trick of superimposing Mercator projections at different scales.
I first became aware of the Dixon elliptic functions through the 1969 special issue (#16) of Cartographia consisting of L. P. Lee's monograph Some Conformal Projections Based on Elliptic Functions which I avidly read in the library of the University I attended.
In 1965, L. P. Lee published a paper with the same title, in which. in addition to discussing other projections based on conventional elliptic integrals, including giving the correction for Adams' projection of the globe on an ellipse, he showed one new projection, based on Dixon elliptic functions, of his own invention, where the world was represented conformally on the surface of a regular tetrahedron.
The 1969 book, however, showed not only that projection, but a number of others, including the one on an octahedron. It also used a different kind of elliptic function, derived through the Schwarz-Christoffel formula, to exhibit a conformal map of the world on the faces of a dodecahedron.
Both the tetrahedron and the dodecahedron get into mathematical waters far too deep for me. (Although Lee did give a polynomial expansion for plotting the tetrahedron, it must be admitted.) But the octahedron is far simpler in comparison, being comparable to the ones from Oscar S. Adams' original work.
I will very briefly mention a very little bit of the mathematics of elliptic integrals relevant to this, as may perhaps help to render intelligible some of the literature concerning them.
The Dixon elliptic functions of the form used here derive from the elliptic curve x^3 + y^3 = 1; only this special case, with another parameter set to zero, is required for conformal mapping to the triangle. Today, elliptic curves are also used in cryptography; this is one curve from the same family.
This relates to a result by H. A. Schwarz from 1864: the integral
_
/ x
| 1
w = | -----------------, du
| 2
| ---
| n n
_/ 0 ( 1 - u )
can be used to map a circle conformally to a regular polygon of n sides. x gives the position of the point on the circle, while w(x) gives the position of the point on the polygon.
This equation, where n=3, is the one from which these Dixon elliptic functions are derived:
_
/ x
| 1
w = | -----------------, du
| 2
| ---
| 3 3
_/ 0 ( 1 - u )
is the basis of the definition of the Dixon elliptic function sm: sm(w) = x. This is the inverse function of the integral; it is the integral itself that is used to draw maps on a triangle.
The formula
3 3
(sm(z)) + (cm(z)) = 1
defines the auxilliary function cm.
This relates to the elliptic curve x^3 + y^3 = 1 in the same way that the formula
2 2 sin x + cos x = 1
relates to the unit circle which has the formula x^2 + y^2 = 1. Note that the notational convention
2 sin x
with the meaning (sin(x))^2 instead of (sin(sin(x)) is also used with sm and cm, although I abstained from presupposing familiarity with this above. This is also done with the Jacobian elliptic functions, which are inverses of the conventional elliptic integrals, as well.
The derivative of sm(x) is the square of cm(x), and the derivative of cm(x) is minus the square of sm(x).
The length of the side of a period rhombus for sm or cm on the complex plane is approximately 1.766638750285..., having the formula:
/ / 1 \ \ 3
| Gamma | --- | |
\ \ 3 / /
--------------------------
___
/
2 / 3 pi
\/
This is as far as I plan to go here as in order to explain the theory of elliptic integrals, I would first have to understand it myself. However, I will mention that there is a more general elliptic function, the Weierstrass elliptic function, in terms of which the Dixon elliptic functions can be expressed.
For practical purposes, the series for the inverse function of sm is what is of interest, and that is:
2 1 4 2 5 1 7 2 5 8 1 10
z + --- * --- z + --- * --- * --- * z + --- * --- * --- * --- * z + ...
3 4 3 6 7 3 6 9 10
It is possible to avoid calculating a series like this using complex arithmetic, but instead to split it into two separate series, one for the real part and one for the imaginary part, of the result by using the representation of a complex number as its magnitude and its argument.
That is, since
ia
z = x + iy = r * e
where r = sqrt(x^2 + y^2) and a = ATAN2(x,y), then
n n ina z = r * e
and n and a are both real numbers, not complex ones,
ix e = cos(x) + i * sin(x)
for any n, the real part of z^n is r^n * cos(n*a), and the imaginary part of z^n is r^n * sin(n*a).
So the series above for the integral may be split into two series, with z^n replaced in one by its real part in each case, and in the other with z^n replaced by its complex part in each case.
ATAN2 is a nice convenient function from FORTRAN; basically, it is the angular part of the result of converting x and y from Cartesian coordinates to polar coordinates; thus, it is an arctangent of y/x, but not necessarily the principal value - it may be any value from -pi to pi, so as to be the angle of the line from the origin to the point (x,y).
This series derives from an integral that transforms the unit circle into a rhombus.
How do we get from there to drawing a map?
We know how to transform a hemisphere to a unit circle: use the Stereographic projection. And the Lagrange projection shows how we can change that from a hemisphere to the whole world - or, as would be useful for the octahedral projection, a lenticular area corresponding to an extent of 90 degrees of longitude.
While I plan to eventually add code for at least one of these projections to my map drawing program, for the time being, here is an image from Adams' work to illustrate this page:
This is another image from that work, showing his projection of the world on a six-pointed star:
As is clear, this projection was very closely related to the octahedral case, only requiring a conformal scale transformation of the world to two-thirds of the world to yield that projection.
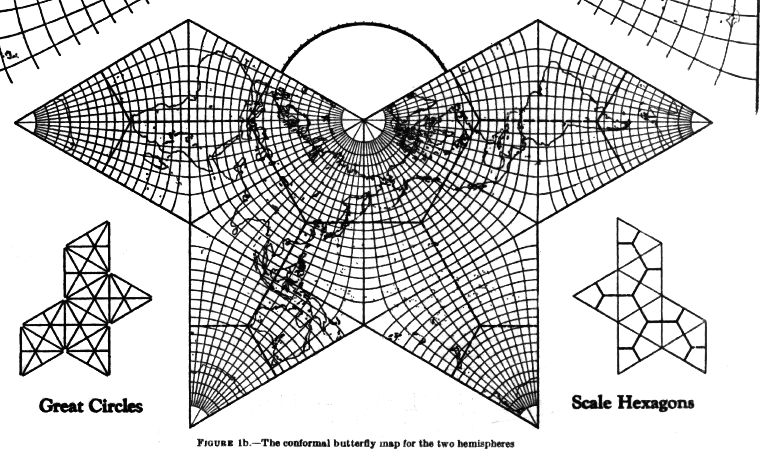
And here is an image of the conformal version of the Cahill butterfly projection. I was able, after a great deal of searching to find one free program (I had earlier found one commercial one) that handles projections based on the Dixon elliptic functions. The program was Map Designer, by Justin Kunimune.
However, while it did include a projection which did, like the conformal version of the Cahill butterfly, map a 60 degree region of the globe to a rhombus, the projection was one different from what I wanted to show here. As a result, I had to take the program's SVG output, convert it to JPEG, and edit it quite heavily, so the image below is not of the best quality, and does not do his program justice.
Because the graticule lines are part of the vector database from which the program works, along with the coastlines, in order to be able to cut the projection the program draw to produce the image, I originally had to choose the central meridian to be 15° W rather than either 20° W as commonly used, or 22°.5 as originally used by Cahill. Because Justin Kunimune released an improved version of Map Designer, however, I was no longer hesitant to make a replacement map in which the now-standard 20° is used, and that is now the one shown above.
The original Butterfly Map by B. J. S. Cahill is an attractive world map; although I liked it, I felt I could not give it proper coverage on my pages for a number of reasons. However, there is an excellent site dedicated to that projection, and thus providing a link to that resource will be more helpful than any limited mention I could provide on these pages.
Incidentally, I noticed that the top part of a triangle of the octahedral version of this projection, as well as the parts of the projection near the 60 degree vertices of the rhombus in other variants, had a strong resemblance to a Lambert conformal conic.
Thus, I wondered if one could approximate this projection, without recourse to elliptic integrals, by stitching together a conventional Lambert conformal with Lambert conformals in two transverse aspects, so as to put the pole of the projection in each of the three corners of the triangle.
The drawing below shows that while this gets close, it doesn't get quite close enough to be unnoticeable.
Also drawn by Map Designer - again, with a significant amount of editing by hand on my part in a paint program - is the conformal projection of the world on the surface of a tetrahedron due to L. P. Lee:
Here, once again from a U. S. Government publication, in this case An Album of Map Projections by Snyder and Voxland, is the Cox Conformal Projection, from 1935:
