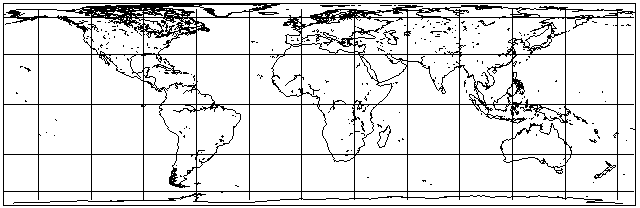
Although this projection is not particularly attractive in appearance, it has sometimes been seriously proposed for actual use, particularly in versions where the map is stretched vertically to a considerable extent.

Its main significance is as an intermediate mathematical step in the construction of some equal-area projections which we will examine later.
However, it can be noted that it doesn't look too bad within about 30 degrees of the Equator, and so it can be used in the transverse case for areas very narrow in longitudinal extent as well. This is useful not only for maps of Chile, or even Argentina, but also for things like gores used to make globes (although the Polyconic projection is the one most commonly used for that purpose) and also for maps showing the stars in the night sky that will be overhead at a certain hour of the evening at a certain time of the year. (For that purpose, though, I would be inclined to use the Gauss Conformal projection, the transverse case of the Mercator.)
This projection's equal-area properties are based on the fact, as shown in this diagram:
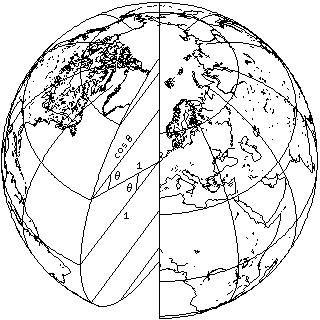
that the width of a degree of longitude is proportional to the cosine of the latitude, while the length of a degree of latitude remains constant.
In the Mercator projection, the latitude scale at any point was stretched by the same amount as the longitude scale had been stretched because the projection was cylindrical, to preserve shape.
In this projection, the latitude scale at any point is instead shrunk to make up for the fact that the longitude scale is stretched, so that the product of the two scales is constant, to preserve area.
Thus, in this case, the equation governing the position of the parallels is found by the following integral:
_n
/
|
| cos(x), dx = sin(n)
|
_/
0
which is a considerably simpler integral than the one that must be solved for the Mercator projection.
As noted above, the cylindrical equal-area projection has been proposed for general use when stretched vertically. A particularly infamous case of this is the Peters projection, invented by one Arno Peters, and made public in 1973, which had aroused considerable controversy. It has standard parallels at 45 degrees.
The Gall Orthographic projection, invented in 1885, is also the equal-area cylindrical projection with standard parallels at 45 degrees; when originally presented, due to a calculation error, the Peters projection was shown with standard parallels of 46 degrees and 2 minutes, although 45 degrees was intended; the difference, however, is too small to see.
I had thought that he had come to his senses, when I heard of a normal and attractive equal-area projection, the Entfernungsbezogene Weltkarte, however, this projection was the work of a different individual merely sharing the same surname, one Aribert Peters, a professional cartographer, unlike Arno Peters, whose original profession was that of a filmmaker.
As it appeared to me that Arno Peters' comments advocating his projection implied that it was the only equal-area projection in existence (!) along with the fact that its appearance was unattractive to me, I was definitely not on his side in the controversy. If one wanted a simple, uninterrupted equal-area projection of the world, and was willing to accept some stretching as the price, it seemed to me that, for example, the Eckert IV projection would achieve the goal of giving tropical countries their due in a far more reasonable way.
Of course, the Mercator projection, by being a simple rectangular grid, does have an advantage which leads some to insist that its only equal that could supplant it is the equal-area cylindrical projection. Because an equal-area cylindrical projection necessarily comes with gross distortion of shapes, I can't agree that this is really a better presentation of "the way the world is", and instead feel we just have to accept the fact that the equal-area property does not lend itself well to cylindrical projections.
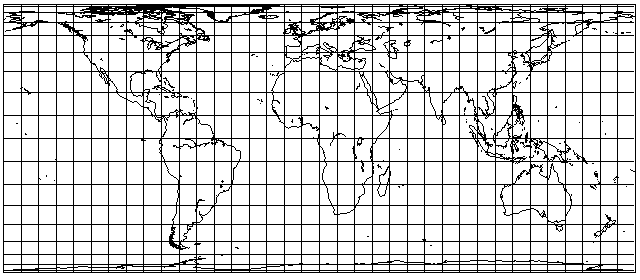
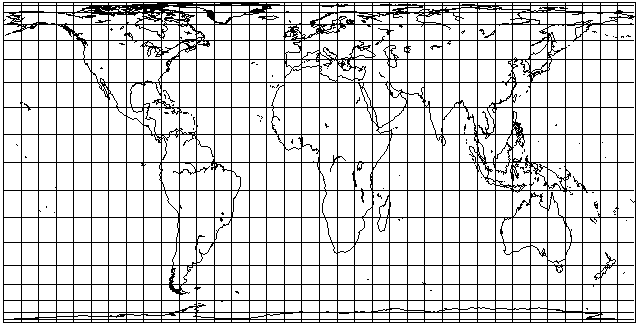
Less controversial stretched forms of the cylindrical equal-area projection, perhaps because they involve a less extreme degree of vertical stretching, include the Behrmann projection, with standard parallels of 30 degrees, and the Hobo-Dyer projection, with standard parallels of 37.5 degrees.
In 1953, Trystan Edwards advocated a form of the cylindrical equal-area projection as something to displace the Mercator; one source gives its standard parallels as being at 50 degrees and 52 minutes, and another gives its standard parallels as being at 37 degrees and 24 minutes. And a third claims that his projection must have been some other projection, because it wasn't really equal-area.
This is what the Behrmann projection looks like:
and this is what the Hobo-Dyer projection looks like:
In addition to the Gall Orthographic, with standard parallels at 45 degrees, Waldo R. Tobler, also a renowned professional cartographer, proposed a version of the equal-area cylindrical projection with standard parallels at about 55.6 degrees. The Balthasart projection is a version with standard parallels at 50 degrees. Thus, there have been serious proposals for equal-area cylindrical projections with higher standard parallels.
If one chooses a standard parallel of 47.5 degrees, somewhere between London and Paris, the resulting Eurocentric version of the cylindrical equal-area projection becomes this:
with extreme vertical stretching in the tropical regions. Of course, this is actually worse than the Peters projection, so it wouldn't be fair to criticize it on the basis of how terrible this projection looks, but this does illustrate that the cylindrical equal-area projection is not capable of being made accurate for northerly regions, and tolerable for equatorial regions, at the same time.
Here is what the Gall Orthographic projection looks like, as drawn by G-Projector:
since the stretching is somewhat less, at least the overall shape of the map is now a rectangle that fits well on a printed page.
My own tastes are such that I would be willing to regard the Behrmann projection as acceptable, but not even the Hobo-Dyer. As to the controversy surrounding the revival of the Gall Orthographic projection by Arno Peters, while I haven't said much about it here, I do touch on it on my page about the Equal Earth Projection.
Also, I just recently found out that maps with South at the top, instead of North, were printed in the Hobo-Dyer projection. Presumably it is one of those that was used as a prop in the episode of the television series Benson where the governor is taken hostage by someone desperate to make his point that this map needs to be used in schools to stop children from having a distorted idea of the world. This plot premise may have been inspired by the book The HAB Theory by Allan W. Eckert, a book which has the form of a novel, but is intended to present the Pole Shift notion also seen in the book 5/5/2000: Ice, the Ultimate Disaster by Richard W. Noone.
Just as we examined transforming from the geodetic longitude on an ellipsoid to an equivalent longitude on a sphere for conformal mapping on the page for the Mercator projection, we can look at the same transformation for the purpose of retaining the equal-area property instead here.
The technical term for the spherical equal-area equovalent latitude is the authalic latitude.
As noted on that page, we have a number like 297 or 298.25 which is the reciprocal of the flattening, which we will represent by the letter g, and the eccentricity, e, can be derived by the formula sqrt( 2/g - (1/g)^2 ).
The formula for the authalic latitude is a little more complicated than that for the conformal equivalent latitude, but it can still be evaluated directly from functions normally available in programming languages and on scientific calculators, that is, the elementary transcendental functions.
As on the page for the Mercator projection, we will use n to stand for the latitude.
Let us define q(x) as follows:
2 sin(x) 1 1 - e sin(x)
q(x) = ( 1 - e ) * ( ---------------------- - ----- * ln ( -------------- ) )
2 2 2*e 1 + e sin(x)
1 - e * ( sin(x) )
Then, the authalic latitude is:
q(n)
n' = arcsine ( -------- )
q(90°)
where 90 degrees may be considered to be another notatiom for pi / 2 so the functions can use radians. And, of course, the sine of 90 degrees is 1, making the formula for q(90°) a simpler one:
2 1 1 1 - e
q(90°) = ( 1 - e ) * ( -------- - ----- * ln ( ------- ) )
2 2*e 1 + e
1 - e
In addition to the conformal latitude and the authalic latitude, three other auxilliary latitudes associated with the ellipsoid are used in cartography.
The rectifying latitude represents the portion of distance along the meridian given by the geodetic latitude.
The parametric latitude is the one where the parallel of latitude on the sphere has the same radius as the parallel of the geodetic latitude on the ellipsoid.
The geocentric latitude is determined by a line from the Earth's center to the point on the surface of the ellipsoid.