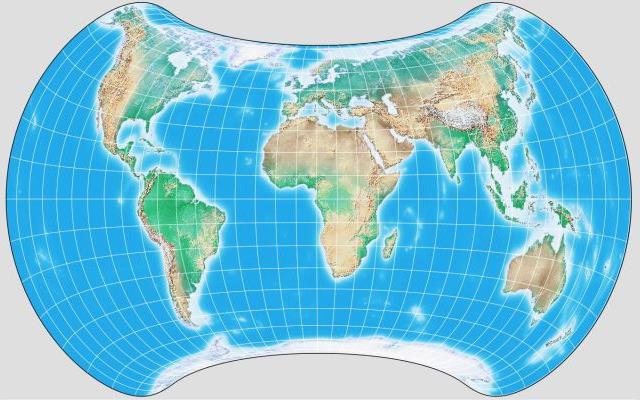
This image of the Strebe projection was drawn for me by G.Projector:
This equal-area projection is designed to minimize angular distortion in the main land areas, placing it in the extreme polar regions and the Pacific Ocean instead.
While formulas are provided for generating the projection directly, it is defined by the following interesting procedure:
Begin with an Eckert IV projection. Draw it, at a reduced size, within a Mollweide projection, and then go from the Mollweide projection back to the globe. Then project the globe on the Hammer-Aitoff projection.
Each step involves an equal-area projection being used, either forwards or backwards, and so the resulting projection is equal-area.
Of course, the Eckert IV projection requires an iterative procedure to calculate the heights of its parallels, but since it is the inverse of the Mollweide that is used, the remainder of the projection can be calculated directly.
However, it appears I must have misunderstood this procedure. Since both the Eckert IV and the Mollweide are pseudocylindrical, the pole lines of the Eckert IV will follow along parallels on the globe after the first two steps. But the pole lines on the Strebe projection are more strongly curved than any parallels on the Hammer-Aitoff projection. This is likely accounted for by the application of a stretch factor somewhere.
This is an interesting map projection, but even though a number of other map projections that look far stranger have achieved wide publicity, I fear that people will tend to ignore it because its overall shape is unconventional.
I learned one important thing from a page on which this projection is described. Its central meridian is 11 degrees East longitude. I had thought that a central meridian of 10 degrees East longitude led to the edge of the map nicely passing through the Bering Strait, but in fact 170 degrees West longitude still passes through the tip of the Chuckchi Peninsula, and 168 degrees West longitude, by a lesser amount, intersects the edge of the Seward peninsula, so if it is desired not to cut either North America or Asia, the edge of the map needs to be at 169 degrees West, which means the center needs to be at 11 degrees East.
The first map I could find online that was detailed enough to allow me to confirm this was a map of school districts in Alaska, of all things.
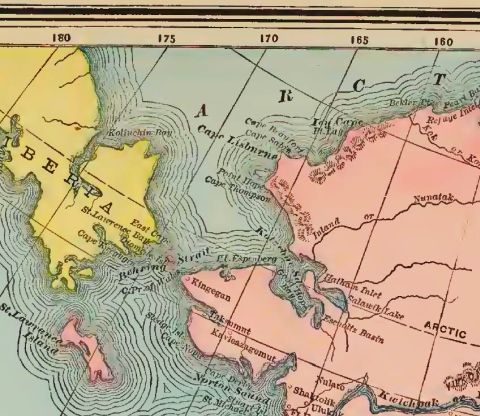
But this portion of a map of Alaska from a very old atlas also makes it visible that the meridian of 170 degrees West longitude cuts through the tip of Siberia.
Although this projection did not excite me as all that much better than, say, a Wagner VII, the Strebe Asymmetric projection which he later developed in 2011 does impress me, as giving the lowest distortion for the major land masses I've seen in any uninterrupted equal-area projection.