This is an interesting although obscure projection. It was used, without being described, in a 1927 book by one Bruno Dietrich for a wide variety of thematic maps. I don't know if I, personally, have seen that book, but it is possible that I had, and then, long after, when I learned of the Van der Grinten IV projection, I may have mistakenly assumed that the maps in that book were on that projection.
A Japanese cartographer, Kozo Kitada, having encountered that book, noted that the projection used in it appeared to be equal-area. On the basis of that as an assumption, and other observed properties of these maps, he worked out what the projection would be.
In addition to the projection being equal-area, the meridians 90 degrees west and east of the central meridian formed a circle, and except for the central meridian, which was a straight line, the other meridians were all circular arcs.
My source for all this information is one forum post by the well-known cartographer Daniel Strebe; I have not found much other information about this projection on the Web.
Based on the properties of the projection noted above, the first step in working out what the projection must be is to determine the areas enclosed by the meridians:

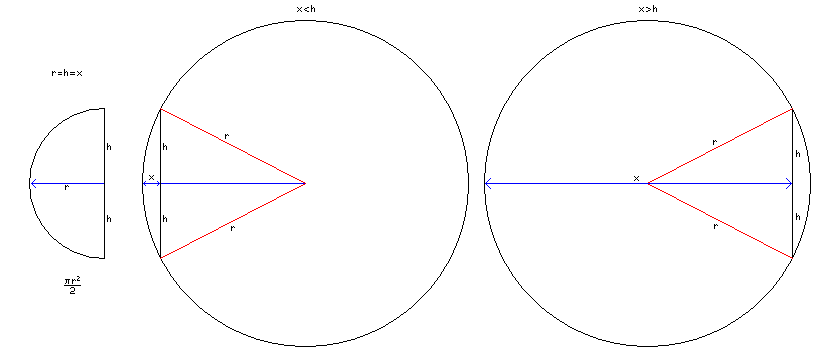
Let the central meridian extend a distance of h above and below the equator. Then, clearly, as shown in the first part of the diagram above, the meridian for 90° W encloses an area of pi times h squared divided by two between itself and the central meridian.
For the projection to be equal-area, the areas enclosed by the other meridians need to be in linear proportion to their longitudes, as compared to the 90° meridian.
Simple geometry allows us to work out the relationship between the area a meridian that is a circular arc encloses between itself and the central meridian.
In the case of a longitude less than 90 degrees, it works out as follows:
The distance from the central meridian at which the meridian crosses the Equator is given by x. Ideally, we would like to find x, given the enclosed area. What we can do easily is find the expression for the area in terms of x.
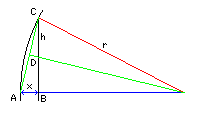
First, we can form a right triangle with x and h as its two lesser sides, with a hypoteneuse of length sqrt( x^2 + h^2 ). A perpendicular from the middle of that hypoteneuse will intersect the center of the circle of which the arc forms a part, and by similar triangles we can see that the radius of that circle, r, must be equal to
__________ __________
/ 2 2 / 2 2
\/ x + h \/ x + h
--------------- * ----------------
x 2
the ratio of the hypoteneuse to the short side, times half the hypoteneuse. Of course, that clearly simplfies to (x^2 + h^2)/2x.
Once we know r, then we can look at the diagram above to find the formula for the area:
The area of the circle as a whole is, of course, pi times r^2.
We are only taking a pie slice of that circle, determined by the arcsine of h/r; the portion is arcsine( h/r ) over 180 degrees or arcsine( h/r ) over pi. So we multiply the area as a whole by that fraction.And from that pie slice, we subtract a triangle, with area h * ( r-x ).
The formula for the area likely is not invertible, so iterative methods will have to be used to find it, as are needed for the Mollweide and the Eckert IV.
Then there is the case of the meridians for angles more than 90° away from the central meridian. It seems to be very similar, but without knowing r in advance, it doesn't seem like we can use the same triangle to find r.
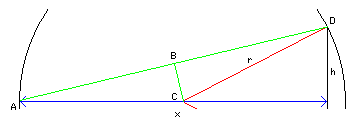
But that's all right, we can work with a different triangle.
Once again, it is a right triangle with x and h as its two short sides, and thus we know that its hypoteneuse has the length sqrt( x^2 + h^2 ).
Divide that hypoteneuse in half, and we have a similar triangle the hypoteneuse of which is of length r, and so here the radius of the circle must be equal to:
__________ __________
/ 2 2 / 2 2
\/ x + h \/ x + h
--------------- * ----------------
x 2
Astonishingly, it works out to exactly the same expression as we saw before, even though the circumstances of its derivation look very different!
Now, however, the area between the meridian and the central meridian is the big part of the circle instead of the small part, so we take the area we worked out above, and subtract it from pi * r^2 to get the new area for this case.
Placing the arcs of longitude, however, might be the easy part. Placing the point for a given latitude along those arcs appears to require a journey into the infinitesimal calculus. (Actually, these days, we just call it "calculus" for short.)
Examining an example of this projection drawn on the web by someone else's computer program, however, I finally reached a simple insight that means the secret of this map projection can be derived with some simple algebra instead of very complicated calculus.
Dividing a meridian of this projection appropriately for it to be equal area would require an understanding of the area along the lune formed by two arcs, both going through the poles of the projection, separated by an infinitesimal distance.
I was loath to try deriving this from geometry.
Then, noting that the Stereographic projection in the equatorial case also has meridians which aref arcs which all go through two poles, I thought that perhaps the way latitude is distributed along these arcs to maintain its conformal property would allow one to derive the thickness of those arcs, which one could then divide to give the equal-area property instead.
And I noticed an interesting starting-point; the arcs for 90 degrees east and west of the central meridian... were equally divided in this projection and in the Stereographic. The central meridian of the Sinusoidal projection is another case where conformality and equality of area are found together, so the width of the infinitesimal lune in that position must resemble a sinusoid.
And then I had the insight that led me to the answer.
If you filled a sinusoid to achieve conformality on a smaller scale, so that by the time you filled it up to 60 degrees of latitude you were only a small part of the way along, the spacing of parallels would look a lot like the Mercator projection. So the fact that the central meridian of the Stereographic is more closely spaced near the equator doesn't have to mean the lune there is different in width distribution from the lune at 90 degrees.
The lunes could be all the same in that respect, and that would make sense. A circle and a sinusoid at the smallest scale look just like parabolas.
And then I took another look at that map on the Dietrich-Kitada projection I had seen online, and, indeed, the intersections of the parallels with the meridians were equally spaced for other meridians as well, not just the ones at 90 degrees.
Thus there are times when it is better to seek insight than to fill many sheets of paper with long calculations.
It did take a lot of debugging before I could make my program plot this equal-area map projection I may have seen many long years ago, and then confused with the Van der Grinten IV, but I finally did it, so I can present an image of it of my very own here:
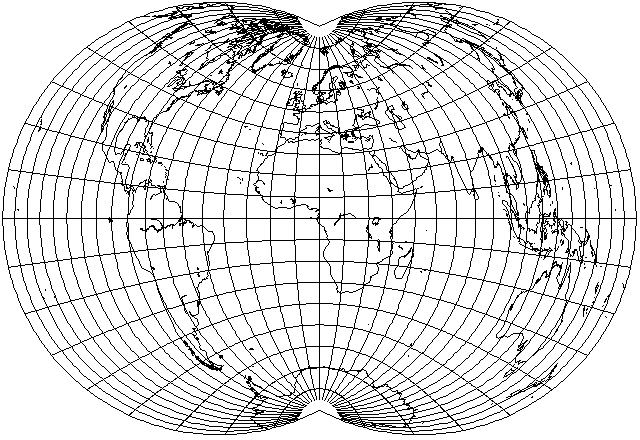
However, I now think that the final step of the analysis above was faulty. Maybe the infinitesimal lunes can be thought of as bounded by paraboloids, but nothing similar is happening to the sinusoid that is involved. Thus, instead of being equally spaced, the spacing of the parallels should resemble that in Craster's Parabolic Equal-Area Projection. That gives the following appearance for the projection:
I will be revising and correcting this page to reflect this in the future.
The initial depiction of the projection above, didn't look all that attractive to me. North and South America, and Australia, were quite badly stretched vertically, reminding me of the Gott projection.
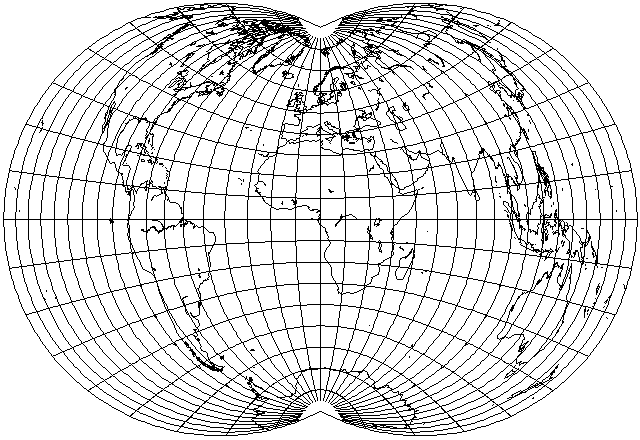
Because the central hemisphere is mapped to a circle, and the scale along the central meridian is uniform, this projection has the same horizontal stretch on the central meridian as the Mollweide does on the Equator. This relationship can be seen explicitly in this diagram:
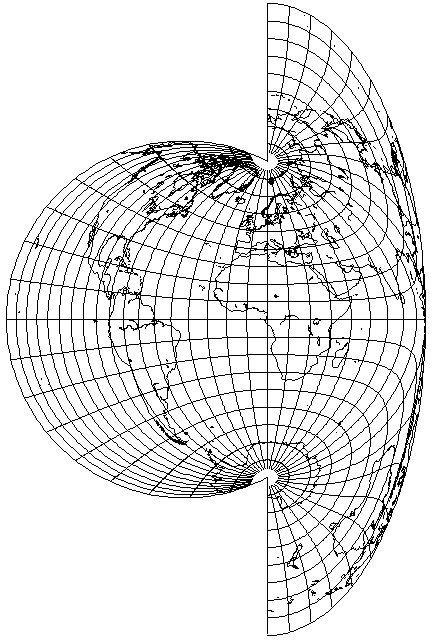
Since this projection has the same horizontal stretch at the prime meridian as the Mollweide has a vertical stretch at the equator, and also, like the Mollweide, it puts its central hemisphere in a circle, I present a transverse aspect of this projection which may make it easier to compare this projection to the Mollweide to see how they relate:
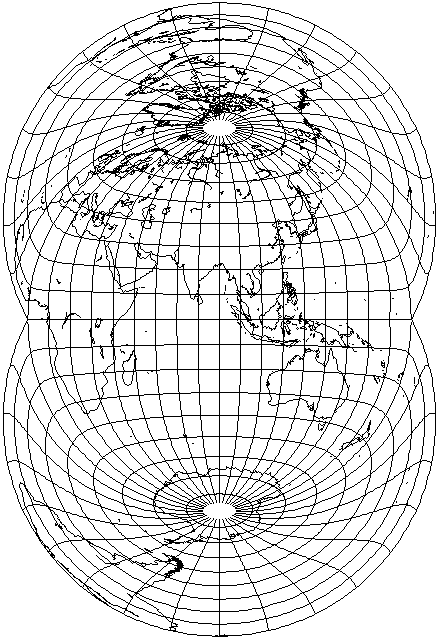
The meridians are nearly straight lines in the center, so the spacing of parallels on the central meridian here, or the spacing of meridians on the Equator in the conventional aspect, will not be similar to the spacing of parallels on the central meridian in the Mollweide.
Since scale is uniform on the central meridian in the Dietrich-Kitada projection, it is uniform on the Equator in this projection. That means that, like the Van der Grinten IV projection, despite having curved parallels, it can be interrupted, which may suggest interesting possibilities.
I am not kidding. An interruptible equal-area projection with curved parallels, and I don't mean Bonne's projection, the parallels do not curve about a common center:
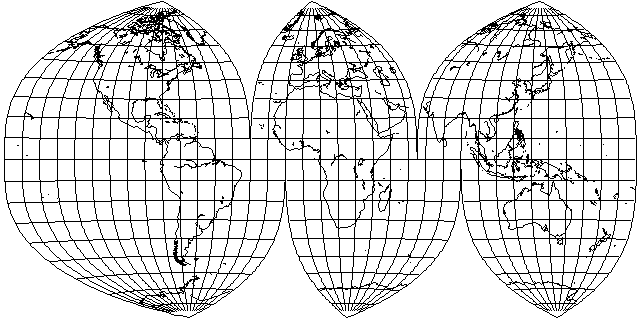
Notice, though, that while the overall shape of the whole projection is the same as that of the Mollweide, a 2:1 ellipse, when the projection is interrupted, the shape of the segments of the interupted projection is very different.
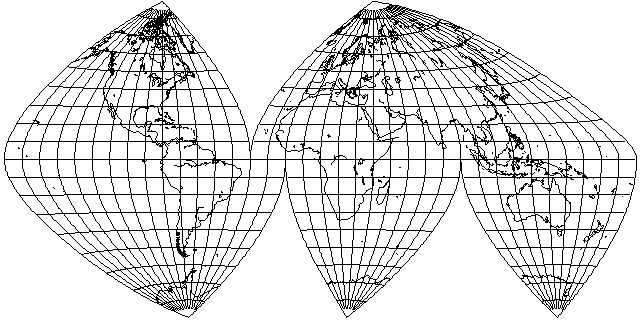
I liked the fact that this projection approaches a cylindrical projection near the Equator. But I had been hoping for more curvature in the parallels. So I tried to apply the same transformation, but using the Sinusoidal projection as a base instead of the Dietrich-Kitada. However, the result not only has only a slight curvature in the parallels, but it looks not much different in overall aspect from the normal Sinusoidal:
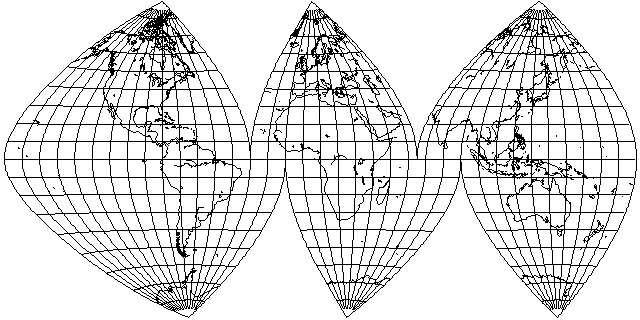
Only when the projection is not interrupted is it obvious that it is derived from the transverse Sinusoidal rather than the conventional one:
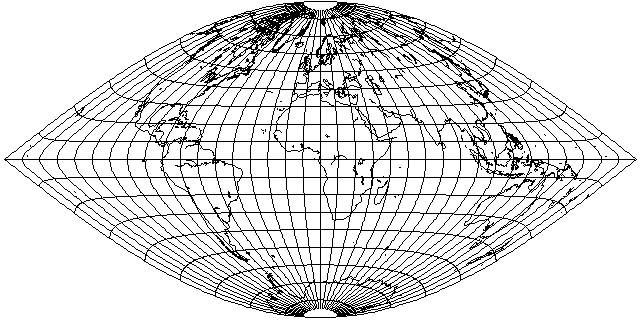
But wait! Perhaps I'm giving up too soon. The map above shows that if I interrupt the map less frequently, then the fact that I'm not just using the normal Sinusoidal projection will start to make a difference.
Well, there it is. The viewer will have to decide if this projection is worthwhile at all.
The transverse Dietrich-Kitada also suggests, however, giving this projection the same treatment as was used to derive the Gott projection from the Bromley-Mollweide.
As we've seen from the page on the Mollweide projection, the Bromley-Mollweide
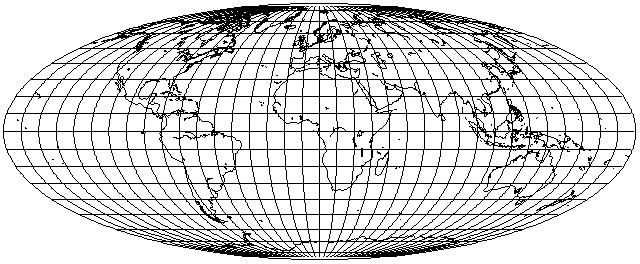
is a modified version of the Mollweide projection which is compressed vertically so that the scale is the same in both directions on the Equator.
While the most obvious use for the Bromley-Mollweide is in making the Mollweide projection harmonize with other projections like the Sinusoidal, another interesting application of the Bromley-Mollweide projection comes from the fact that it can, of course, also have a transverse aspect:
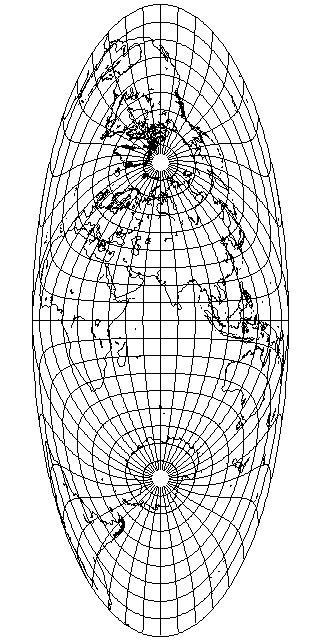
The Eastern Hemisphere, which forms the central part of the map, is a hemisphere, mapped to an ellipse, with uniform scale along its central meridian. If one takes that map of a hemisphere, and derives a new projection from it, the way the Hammer-Aitoff projection is derived from a hemisphere of the Lambert Azimuthal Equal-Area projection, one obtains the Gott Equal-Area Elliptical projection, devised by J. Richard Gott III (the same J. Richard Gott III known for the Doomsday Argument?), which looks like this (once again, as drawn with G-Projector rather than on my own program):
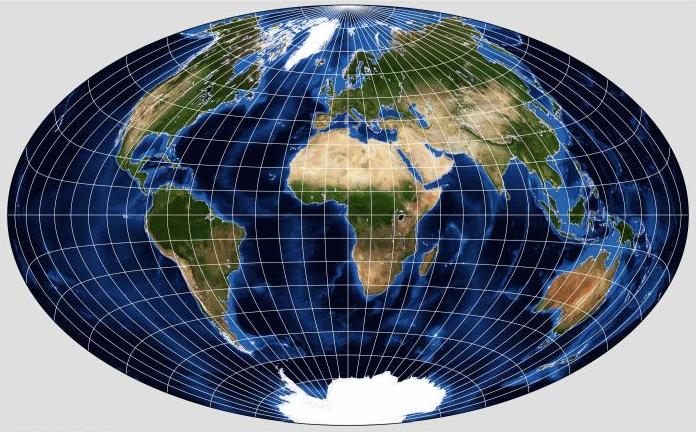
To me, the obvious use for the Gott projection, and the transverse Bromley-Mollweide, would be to create a map similar to the Oxford projection, using those projections with the Sinusoidal, instead of using Adams' Equal-Area projection with the Lambert Azimuthal Equal-Area and the Hammer-Aitoff. However, this was not the reason why the Gott projection was proposed; instead, it was proposed because the uniformity of scale in the central meridian helped to minimize distance areas within the projection.
The result, derived from the low-distortion portions of this projection, might be satisfactory; in addition, as it would have a central portion that behaves like an equal-area cylindrical projection, despite placing the world on an ellipse (!) its distribution of errors might be very useful - unlike that of the Dietrich-Kitata projection, which almost seems to be perverse, as illustrated by my attempts below to find a useful aspect for it.
Here is the projection which is obtained in this manner:
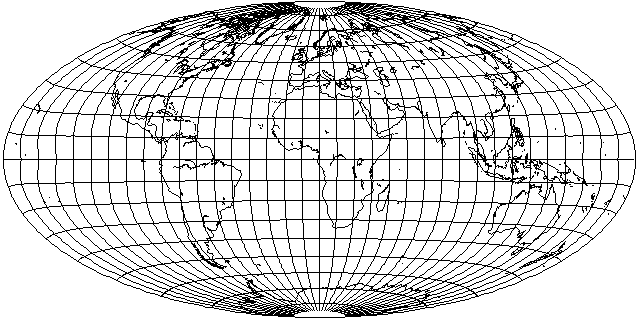
One does not need to search far for an aspect to make this projection look good; thus, using the same aspect used for Bartholomew's Nordic projection,
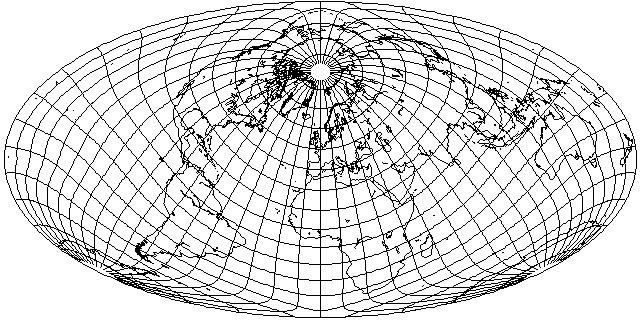
one gets this result - which allows Australia and New Zealand to have an excellent appearance for this kind of map.
However, that doesn't make this projection better than Bartholomew's Nordic - Europe is stretched vertically on this map, the same as it would be on an oblique Mollweide, which was avoided by Bartholomew when he used the Hammer-Aitoff. So perhaps I should try substituting this projection for the Mollweide in Bartholomew's Atlantis projection instead:
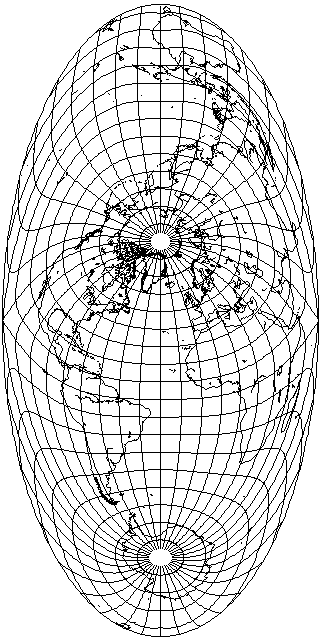
The distortion is greater for the southern part of Asia and the eastern part of Africa. Australia is stretched horizontally, whereas it's stretched vertically in the original Atlantis based on the Mollweide. Canada seems to look better.
Another possibility comes from the fact that not only is the scale along the Equator uniform, but, necessarily as a consequence of its shape, that scale is the same as that of the Mollweide projection; thus, the two may be combined
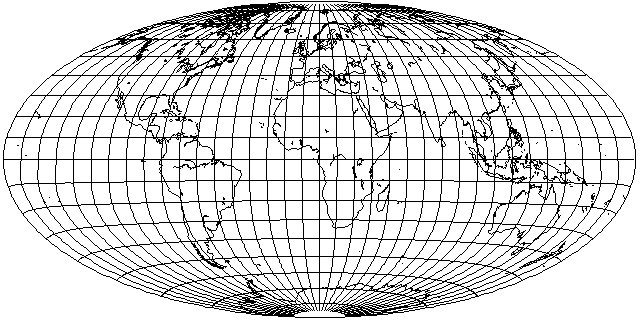
as shown above, with the Southern hemisphere on this projection, and the Northern hemisphere on the Mollweide.
However, different projections have different areas of high and low distortion. Thus, Bartholomew's Atlantis projection carefully takes advantage of where distortion is lowest on the Mollweide projection. So perhaps the fault isn't with the Dietrich-Kitada projection, but how I chose to use it. So if I move the standard parallel into the Atlantic ocean:
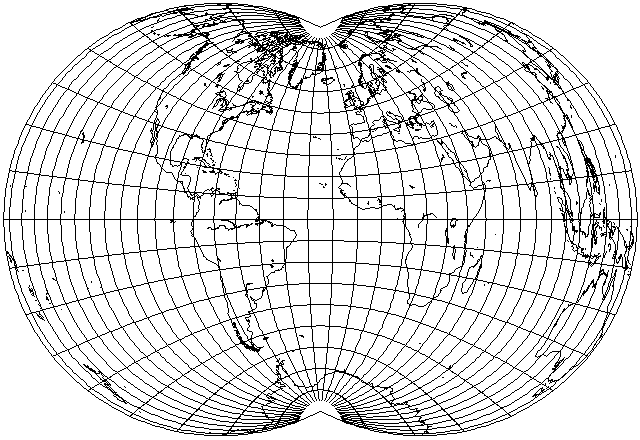
then the United States and Europe are moved into the lowest-distortion areas of the projection, although Australia and Japan do not fare well.
If the distribution of error in this projection does not lend itself well to maps of the Western world, what about a map from the viewpoint of China? Sometimes Chinese maps of the world use 150 degrees East as the central meridian, which puts China significantly off center, so as not to have the edge of the map dividing the Americas into two pieces.
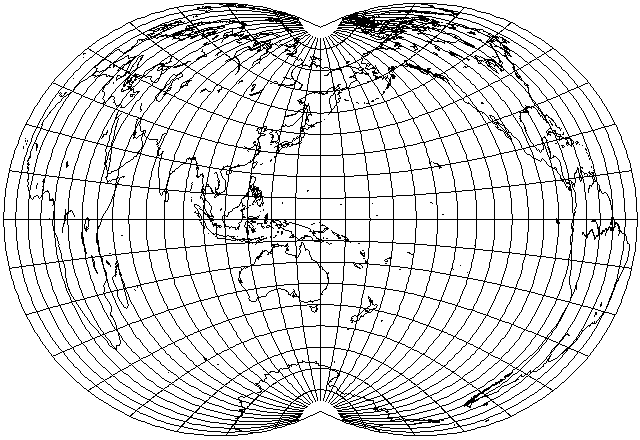
Only the Eastern part of China is in the low-distortion area, and too much of the rest of the world has very high distortion, so this doesn't seem to work either.
Trying a transverse aspect of the projection is also no more successful,
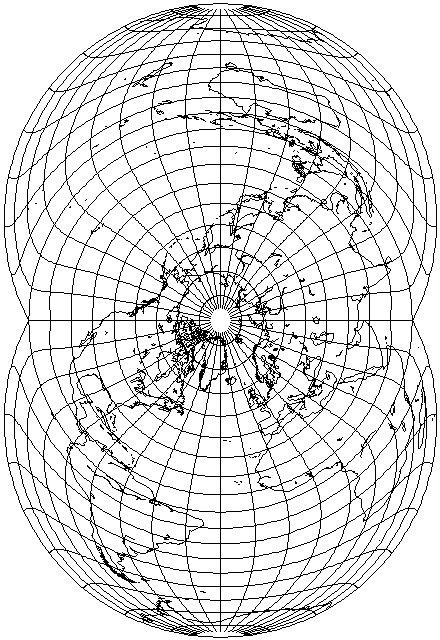
despite the Eastern Seabord of North America and Western Europe being in the parts of the projection with least distortion, but it makes it more apparent how angular error is distributed through the projection; while the center is too wide (or too tall in the image above, where the projection is rotated sideways), beyond the circular region in the center of the projection, error appears to increase rapidly.
Although with no expectation of success, I thought I would make one last attempt, using the Dietrich-Kitada projection in the same aspect that Bartholomew used with the Hammer-Aitoff projection for his Nordic projection, and that was previously used with a Mollweide:
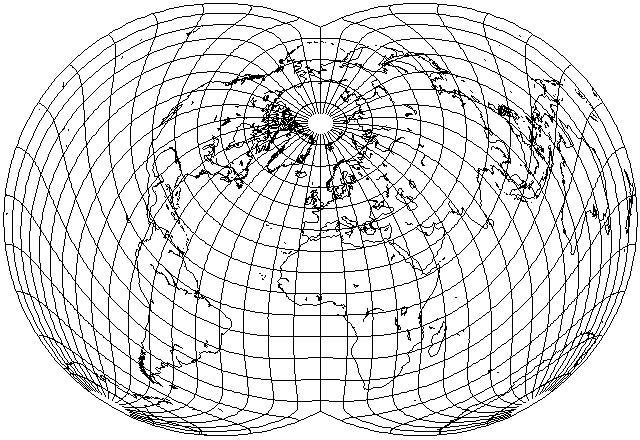
Only Australia fares so badly as to be unacceptable in this aspect. But this aspect shows something strange about this projection: in a large area, from 10 degrees North latitude to 45 degrees South latitude, and from 90 degrees West longitude to 90 degrees East longitude, the meridians are nearly vertical, which is something I never expected.
In any case, this hints at a possibility for an aspect in which this map, despite its seemingly perverse distribution of error, would be tolerable for a world map:
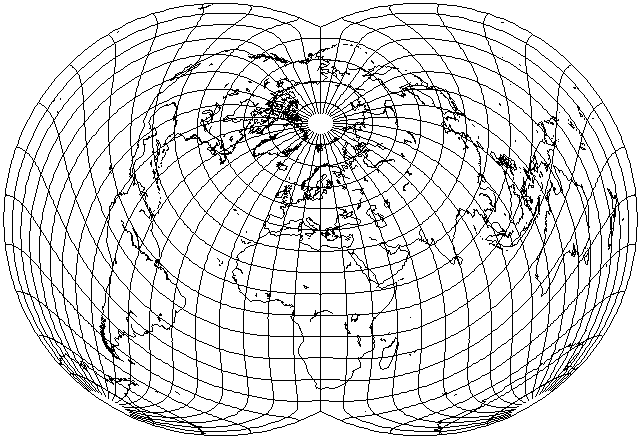
Australia and South America are very definitely competing, but a compromise of sorts is possible.
If the projection is tilted forwards 50 degrees instead of 45, however,
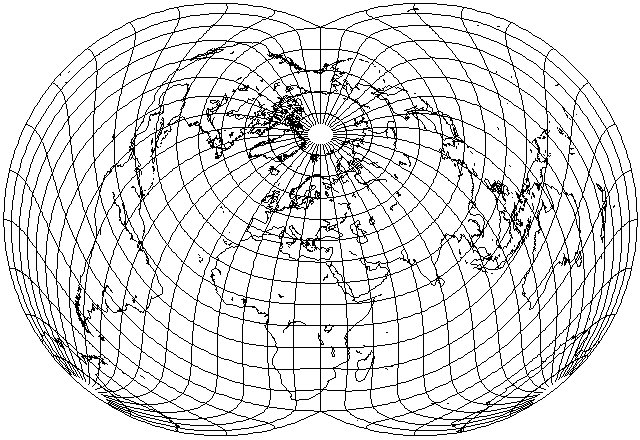
then it becomes possible to favor Australia a little more at the expense of South America without causing severe distortion in North America. So this demonstrates that it is possible to fit a world map to the peculiarities of the Dietrich-Kitada projection.
What happens if we try this orientation with the new projection derived from the Dietrich-Kitada shown above?
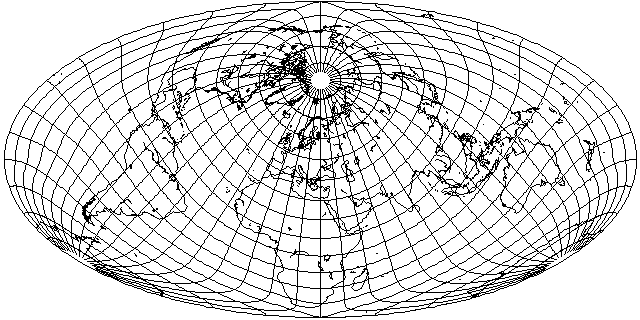
Australia and South America certainly look much better.
But while North America fared well in the Dietrich-Kitada, it is stretched unacceptably on this projection. Also, I will need to have a clearer idea of how this new projection differs from the Mollweide to understand how to make best use of it.
Also, of course, since the Dietrich-Kitada projection is expanded across the central meridian by the same factor that the Mollweide is expanded across the Equator, the option of giving it a compensating stretch, as was done with the Bromley-Mollweide projection, exists:
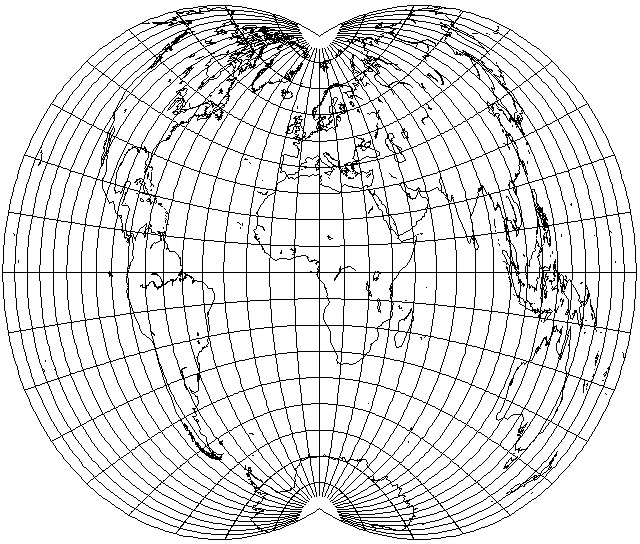
As this does not improve the general appearance of the projection, worsening the excessive vertical stretch at the edges, it is, of course, only useful for special purposes, such as attaching this projection on one side to the Sinusoidal on the other.
If the problem is that there is too much vertical stretching at the edges of the map, then despite the fact that there is already horizontal stretching in the center, would still more horizontal stretch bring about a better balance?
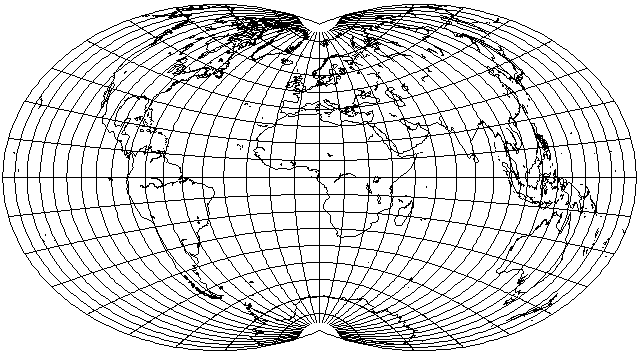
As this diagram shows, a 25% horizontal stretch is going too far; while a smaller horizontal stretch might be beneficial, though, it also shows that it wouldn't be enough to provide real relief to the edges of the map.
Not only is the Dietrich-Kitada projection itself very obscure, but it belongs to a select group of projections, almost all of which are obscure.
The Globular projection was seen commonly in atlases, as a very easy way to draw a passable hemisphere in the Equatorial case, so it isn't obscure, but although it can be theoretically extended to cover the whole world, that is almost never done; if it is done, the result is another "apple-shaped" map of the world:
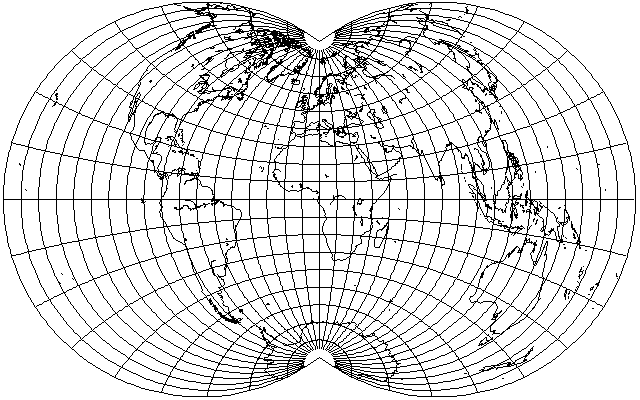
And then there is Henri Bouthillier de Beaumont's modification of the Globular, intended as a whole-world projection; this one is obscure indeed:
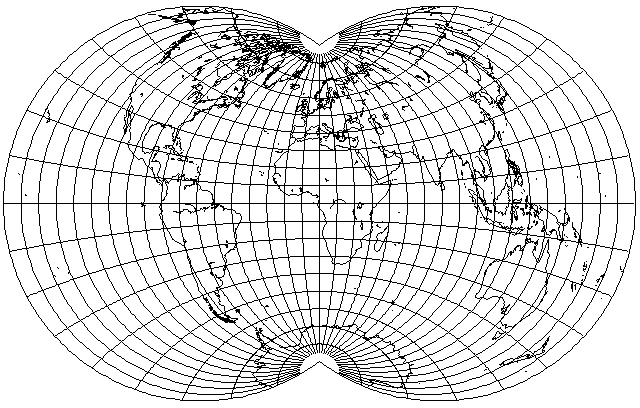
An apple-shaped conventional projection that was designed to show a map of the whole world is the Van der Grinten IV projection, but unlike its more famous cousin that maps the world into a circle, this one is relatively obscure:
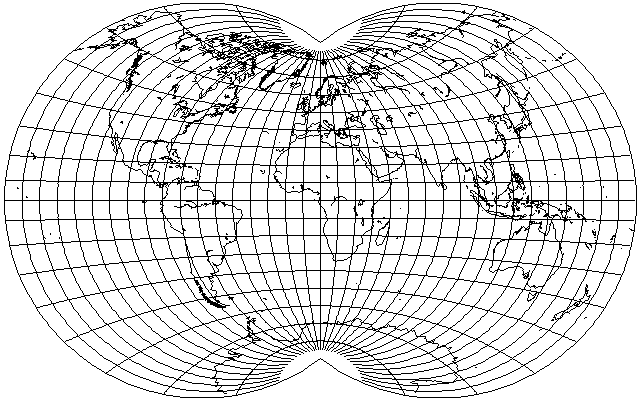
And then there's a conformal apple-shaped projection. No, I don't mean August's Conformal Projection of the World on a Two-Cusped Epicycloid or the Eisenlohr; as the poles are cusps on those projections, so that conformality extends even to them, I would treat that as a slightly different shape. But Lagrange's Projection, if the world only squeezed into a Stereographic projection of two-thirds of the world instead of a hemisphere, is also apple shaped:
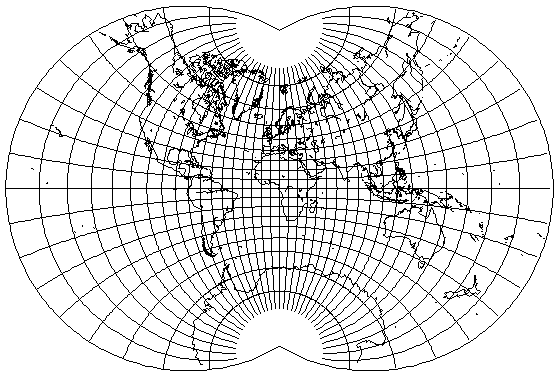
Although apple-shaped, its shape is slightly different from that of most of the other apple-shaped projections shown here (that of the Dietrich-Kitada projection is also different). To give it the same shape, instead of using 240° of the circle, one can use 253.73979529... degrees to obtain this map:
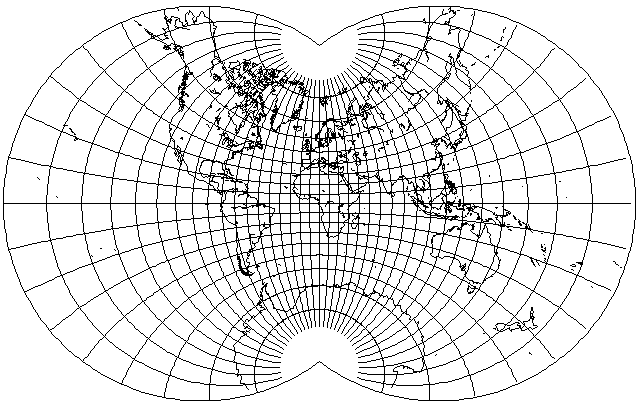
So if you should ever encounter a world map with an apple-shape, you should be able to identify it with the help of this page. (I remember glimpsing one on a computer screen in one of the James Bond movies; I think it was in the Pierce Brosnan era; I haven't found an image online to be able to identify it from.)